When designing electronic circuits, you usually have to solve the problem of amplifying signals - increasing their amplitude or power. But there are situations when the signal level must, on the contrary, be weakened. And this task is not as simple as it seems at first glance.

Contents
What is an Attenuator and How It Works
An attenuator is a device used to deliberately and normally reduce the amplitude or power of an input signal without affecting its shape.
The basic principle of attenuators used in RF applications is voltage divider with resistors or capacitors. The input signal is distributed between the resistors in proportion to the resistances. The simplest solution is a divider of two resistors. Such an attenuator is called an L-shaped attenuator (L-shaped in foreign technical literature). The input and output can be any side of this asymmetrical device. The feature of the L-shaped attenuator is the low loss in input/output matching.
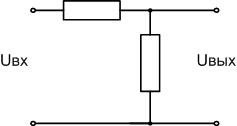
Types of attenuators
In practice, the L-attenuator is used not so often - mainly to match the input and output impedances. Much more widely used for normalized attenuation of signals are devices of P-type (in foreign literature Pi - from the Latin letter π) and T-type. This principle allows you to create devices with the same input and output impedance (but if necessary can be different).

The figure shows asymmetrical devices. The source and load to them must be connected with unbalanced lines - coaxial cables, etc. on either side.
For symmetrical lines (twisted pair, etc.), symmetrical circuits are used - sometimes called H- and O-type attenuators, although these are just a variation of the previous devices.
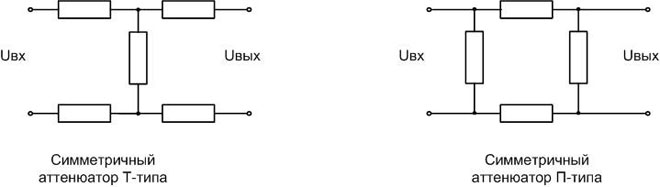
By adding one (two) resistors, a T- (H-) type attenuator becomes a bridge type.
Attenuators are industrially available as complete devices with connectors for connection, but they can also be made on a printed circuit board as part of a general circuit. Resistive and capacitive attenuators have a major advantage - they do not contain nonlinear elements, which does not distort the signal and does not lead to the appearance of new harmonics in the spectrum and to the disappearance of existing ones.
In addition to resistive attenuators there are other types of attenuators. Commonly used in industrial applications are:
- Limiting and polarizing attenuators - based on the structural properties of waveguides;
- absorption attenuators - signal attenuation is caused by absorption of power by specially selected materials;
- optical attenuators;
These types of devices are used in microwave technology and in the light frequency range. At low and radio frequencies, attenuators based on resistors and capacitors are used.
Basic Characteristics
The attenuation coefficient is the main parameter that determines the properties of attenuators. This is measured in decibels. To understand how many times the signal amplitude decreases after passing through the attenuating circuit, you must recalculate the coefficient from decibels to times. At the output of a device that reduces the signal amplitude by N decibels, the voltage will be M times less:
M=10(N/20) (for power, M=10(N/10)) .
Inverse recalculation:
N=20⋅log10(M) (for power N=10⋅log10(M)).
So, for an attenuator with Kosl=-3 dB (the coefficient is always negative, since the value is always decreasing) the output signal will have an amplitude of 0.708 of the original. And if the output amplitude is half the original amplitude, then the Kosl is approximately equal to -6 dB.
Formulas are quite complicated to calculate in your mind, so it is better to use online calculators, of which there are many on the Internet.
For adjustable devices (stepped or smooth), the setting limits are specified.
Another important parameter is the wave impedance (impedance) on the input and output (they may coincide). Related to this impedance is a characteristic such as the Standing Wave Ratio (SWR), which is often indicated on commercially manufactured products. For a purely active load, this coefficient is calculated by the formula:
- VSW=ρ/R if ρ>R, where R is the load impedance and ρ is the line wave impedance.
- VSW= R/ρ if ρ
VSW is always greater than or equal to 1. If R=ρ, all power is transferred to the load. The more these values differ, the greater the losses. So, at VSW=1,2 99 % of power will reach the load, and at VSW=3 - already 75 %. If you connect a 75-ohm attenuator to a 50-ohm cable (or vice versa) the VSW=1.5 and the loss will be 4%.
Of the other important characteristics we should mention:
- operating frequency range;
- Maximum power.
Also important is such a parameter as accuracy - it means the allowable deviation of attenuation from the nominal. For industrial attenuators, the characteristics are printed on the case.
In some cases, the power of the device is important. The energy that does not reach the consumer is dissipated on the elements of the attenuator, so it is critical not to overload.
There are formulas for calculating the basic characteristics of resistive attenuators of various designs, but they are cumbersome and contain logarithms. Therefore, to use them you need at least a calculator. Therefore, it is more convenient to use special programs (including online ones) for self-calculation.
Adjustable attenuators
The attenuation coefficient and VSW is affected by the rating of all the elements that make up the attenuator, so create devices with resistors with continuously adjustable parameters is difficult. By changing the attenuation, it is necessary to adjust the VSW and vice versa. Such problems can be solved by using amplifiers with a gain less than 1.
Such devices are built with transistors or OP-AMPSSuch amplifiers can be built with transistors or Op-Amps, but the problem of linearity arises. It is not easy to create an amplifier which does not distort the signal shape over a wide frequency range. Much more common is step control - the attenuators are connected in series and their attenuation is added together. Those circuits that need to be attenuated are bypassed (relay contacts etc.). Thus, the desired attenuation coefficient is gained without changing the wave impedance.
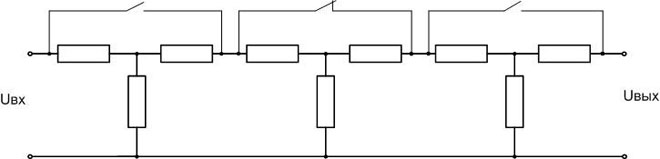
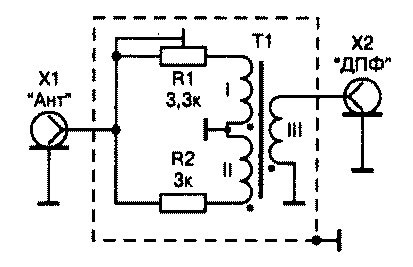
There are designs of devices for attenuating the signal with smooth adjustment, built on broadband transformers (BPT). They are used in amateur communications when the input/output matching requirements are low.
Smooth tuning of waveguide attenuators is achieved by changing the geometric dimensions. Optical attenuators are also available with smooth tuning of attenuation, but such devices have a rather complicated design because they contain a system of lenses, optical filters, etc.
Applications
If the attenuator has different input and output impedances, then in addition to the function of attenuation, it can act as a matching device. For example, if you need to connect 75 ohm and 50 ohm cables, you can put a properly rated one between them and together with the normalized attenuation you can correct the degree of matching.
In receiving technology attenuators are used to avoid overloading the input circuits with powerful side emissions. In some cases, attenuating the interfering signal even simultaneously with a weak useful signal can improve reception quality by reducing the level of intermodulation noise.
In measurement applications, attenuators can be used as decoupling to reduce the effect of the load on the reference signal source. Optical attenuators are widely used in testing transmit/receive equipment for fiber-optic communication lines. They are used to simulate the attenuation in a real line and determine the conditions and boundaries of stable communication.
In audio engineering, attenuators are used as power control devices. Unlike potentiometers, they do this with less energy loss. Here it is easier to provide smooth regulation, because the wave impedance does not matter - only the attenuation matters. In television cable networks, attenuators eliminate overloading of TV inputs and allow the transmission quality to be maintained regardless of reception conditions.
Being not the most complicated device, the attenuator finds the widest application in radio-frequency circuits and allows to solve various problems. At microwave and optical frequencies, these devices are built differently, and they are complex industrial assemblies.
Related articles: