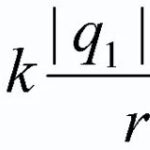The Lorentz force and the left-hand rule. The motion of charged particles in a magnetic field

Placed in a magnetic field conductor...through which an electric current... an electric currentis influenced by the Ampere force $F_A$ , and its magnitude can be calculated by the following formula:

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

where $I$ и $l$ - current strength and length of the conductor, $B$ - the induction of the magnetic field, $\alpha$ - the angle between the directions of current and magnetic induction. So why is this happening?

Lorentz force. The motion of a charged particle in a magnetic field.

Contents

1 What is the Lorentz force - definition, when it occurs, getting the formula
2 Determining the direction of the Lorentz force using the left hand rule
3 Movement of a charged particle in a magnetic field
4 Applications of Lorentz force in engineering

What is the Lorentz force - definition, when it arises, getting the formula

It is known that electric current is the ordered movement of charged particles. It has also been established that while moving in a magnetic field, each of these particles is subject to a force. For a force to occur, the particle must be in motion.

The Lorentz force is the force that acts on an electrically charged particle as it moves in a magnetic field. Its direction is orthogonal to the plane in which the velocity vectors of the particle and the magnetic field strength lie. The Lorentz force is the Ampere force. Knowing it, we can derive a formula for the Lorentz force.

The time required for a particle to traverse a stretch of conductor, $t = \frac {l}{v}$ where $l$ - is the length of the segment, $v$ - the velocity of the particle. The total charge carried during this time through the cross section of the conductor, $Q = I\cdot t$ . Substituting here the value of time from the previous equality, we have

$Q = \frac {I\cdot l}{v}$ (2)

At the same time $F_A=F_L\\cdot N$ where $N$ - is the number of particles in the considered conductor. At the same time $N = \frac {Q}{q}$ where $q$ - is the charge of one particle. By substituting into the formula the value of $Q$ from (2), one can obtain:

$N = \frac {I\cdot l}{v\cdot q}$

Thus,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Using (1), the previous expression can be written as

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

After cuts and transfers the formula for calculation of the Lorentz force appears

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Given that the formula is written for the modulus of the force, it should be written as follows:

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Since $sin\alpha = sin(180^{\circ} -\alpha)$ , it does not matter for the calculation of the Lorentz modulus whether the velocity is directed in the direction of the current force or against it, and we can say that $\alpha$ - is the angle formed by the velocity vectors of the particle and the magnetic induction.

Writing the formula in vector form would look as follows:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}$

$[\vec{v}\times \vec{B}$ - is the vector product, the result of which is a vector with a modulus equal to $v\cdot B\cdot sin\alpha$ .

Based on formula (3), we can conclude that the Lorentz force is maximal in the case of perpendicularity of directions of electric current and magnetic field, that is at $\alpha = 90^{\circ}$ and disappear when they are parallel ( $\alpha = 0^{\\circ}$ ).

Remember that in order to provide a correct quantitative answer - for example, when solving problems - one should use SI units, in which the magnetic induction is measured in teslas (1 Tesla = 1 kg-c⁻²-А⁻¹), force in newtons (1 N = 1 kg-m/s²), current in amperes, charge in coulons (1 Cl = 1 A-s), length in meters, speed in m/s.

Determining the direction of the Lorentz force using the left-hand rule

Since in the world of macro objects the Lorentz force appears as an Ampere force, we can use the left hand rule to determine its direction.

Determining the direction of the Lorentz force using the left hand rule.

If you place your left hand so that your open palm is perpendicular to and against the magnetic field lines, the four fingers should be extended in the direction of the current, then the Lorentz force will be directed to where your thumb, which should be bent, is pointing.

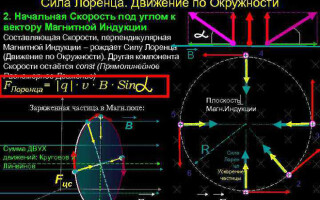
Movement of a charged particle in a magnetic field

In the simplest case, i.e. with orthogonality of vectors of magnetic induction and velocity of the particle, the Lorentz force, being perpendicular to the velocity vector, can only change its direction. The magnitude of velocity, therefore, and energy will remain unchanged. So the Lorentz force acts by analogy with the centripetal force in mechanics, and the particle moves in a circle.

According to Newton's II law ( $F = m\cdot a$ ) we can determine the radius of rotation of the particle:

$N = \frac {m\cdot v}{q\cdot B}$ .

It should be noted that as the specific charge of the particle changes ( $\frac {q}{m}$ ), the radius also changes.

In this case, the period of rotation T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . It does not depend on velocity, so the mutual position of particles with different velocities will be the same.

The motion of a charged particle in a homogeneous magnetic field.

In the more complicated case, when the angle between particle's velocity and magnetic field strength is arbitrary, it will move along a helical trajectory - progressively at the expense of the velocity component directed parallel to the field, and along the circumference under the influence of its perpendicular component.

Application of the Lorentz force in engineering

Kinescope

The kinescope, which until recently, when it was replaced by the LCD (flat screen), was in every TV set, could not work without the Lorentz force. To form a television image on the screen from a narrow flow of electrons, deflection coils are used to create a linearly varying magnetic field. The line coils move the electron beam from left to right and back, the frame coils are responsible for the vertical movement, moving the beam running horizontally from top to bottom. The same principle is used in oscilloscopes - for studying alternating electrical voltages.

Mass spectrograph

A mass spectrograph is a device that uses the dependence of the rotation radius of a charged particle on its specific charge. The principle of its operation is as follows:

A source of charged particles, which gain speed by means of an artificially created electric field, is placed in a vacuum chamber to eliminate the influence of air molecules. The particles fly out of the source and, passing through an arc of a circle, hit a photographic plate, leaving traces on it. Depending on the specific charge, the trajectory radius and, therefore, the point of impact changes. This radius is easy to measure, and knowing it, you can calculate the mass of the particle. Using a mass spectrograph, for example, the composition of the lunar soil was studied.

Cyclotron

The independence of the period, and hence the rotation frequency of a charged particle from its speed in the presence of a magnetic field is used in an apparatus called a cyclotron, designed to accelerate particles to high speeds. The cyclotron is two hollow metal half-cylinders, duants (each one is shaped like a Latin letter D), placed with their straight sides facing each other at a short distance.

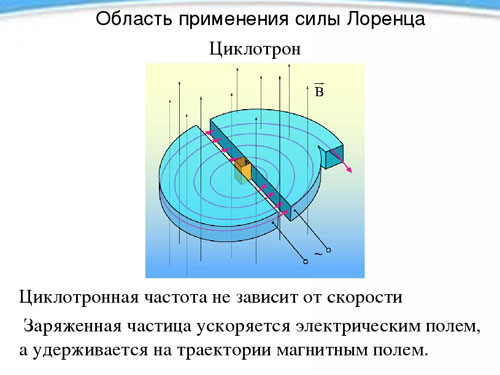
Cyclotron - application of the Lorentz force.

The duants are placed in a constant homogeneous magnetic field, and between them an alternating electric field is created, the frequency of which is equal to the frequency of particle rotation, determined by the magnetic field strength and the specific charge. Being exposed to the electric field twice during the rotation period (during the transition from one duant to another), the particle is accelerated each time, increasing the trajectory radius, and at a certain moment, having gained the necessary velocity, it flies out of the device through the hole. In this way one can accelerate a proton to an energy of 20 MeVmega electronvolt).

Magnetron

A device called a magnetron, which is installed in every microwave ovenis another representative of devices that use the Lorentz force. The magnetron is used to create a powerful microwave field that heats the internal volume of the oven where the food is placed. The magnets included in it correct the trajectory of electrons inside the device.

Earth's magnetic field

And in nature, the Lorentz force plays an extremely important role for mankind. Its presence allows the Earth's magnetic field to protect humans from the deadly ionizing radiation of space. The field prevents charged particles from bombarding the planet's surface, forcing them to change direction.