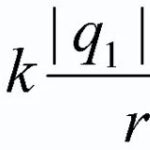ローレンツ力と左手の法則。磁場中の荷電粒子の運動

磁場に置かれる導体...電流が... 電流アンペア力の影響を受ける $F_A$ であり、その大きさは次の式で計算できます。

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

どこ $私$ と $l$ - 導体の電流強度と長さ、 $B$ - 磁場の誘導、 $\アルファ$ - 電流の方向と磁気誘導の間の角度。では、なぜこれが起こっているのですか？

ローレンツ力。磁場中の荷電粒子の動き。

コンテンツ

1 ローレンツ力とは - 定義、発生時に式を取得する
2 左手の法則を使用してローレンツ力の方向を決定する
3 磁場中の荷電粒子の動き
4 工学におけるローレンツ力の応用

ローレンツ力とは - 定義、発生した場合、式を取得する

電流は荷電粒子の秩序ある運動であることが知られています。また、磁場中を移動している間、これらの粒子のそれぞれが力を受けることも確立されています。力が発生するには、粒子が動いている必要があります。

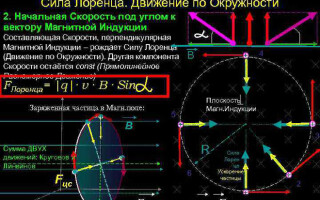
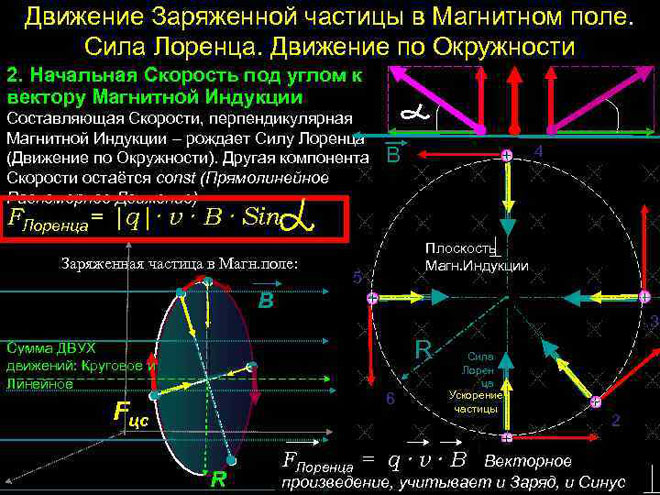
ローレンツ力は、荷電粒子が磁場内を移動するときに作用する力です。その方向は、粒子の速度ベクトルと磁場強度が存在する平面に直交します。ローレンツ力はアンペア力です。それを知っていれば、ローレンツ力の式を導き出すことができます。

粒子が導体のストレッチを横切るのに必要な時間、 $t = \frac {l}{v}$ どこ $l$ - はセグメントの長さです。 $v$ - 粒子の速度。この間に導体の断面を通過する総電荷、 $Q = I\cdot t$ .ここで前の等式からの時間の値を代入すると、次のようになります。

$Q = \frac {I\cdot l}{v}$ (2)

同時に $F_A=F_L\cdot N$ どこ $N$ - 考慮される導体内の粒子の数です。同時に $N = \frac {Q}{q}$ どこ $q$ - は 1 つの粒子の電荷です。の値を式に代入することにより、 $Q$ (2) から、以下を得ることができます。

$N = \frac {I\cdot l}{v\cdot q}$

したがって、

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

(1) を使用すると、前の式は次のように記述できます。

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

ローレンツ力の計算式が表示されます。

$F_L = q\cdot v\cdot B\cdot sin\alpha$

式が力のモジュラスに対して書かれていることを考えると、次のように書く必要があります。

また読む：アンペアをワットに変換して元に戻すには?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

以来 $sin\alpha = sin(180^{\circ} -\alpha)$ , ローレンツ係数の計算では、速度が現在の力の方向に向けられているか、逆に向けられているかは問題ではなく、次のように言えます。 $\アルファ$ - は、粒子の速度ベクトルと磁気誘導によって形成される角度です。

数式をベクトル形式で記述すると、次のようになります。

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}$

$[\vec{v}\times \vec{B}$ - はベクトル積であり、その結果は次の係数を持つベクトルになります。 $v\cdot B\cdot sin\alpha$ .

式（3）に基づいて、ローレンツ力は、電流と磁場の方向が垂直である場合に最大になると結論付けることができます。 $\alpha = 90^{\circ}$ 平行になると消えます( $\alpha = 0^{\circ}$ ).

たとえば、問題を解決するときなど、正しい定量的な答えを提供するには、磁気誘導がテスラ (1 テスラ = 1 kg-c) で測定される SI 単位を使用する必要があります。⁻²-А⁻¹)、ニュートン単位の力 (1 N = 1 kg-m/s²)、電流 (アンペア)、電荷 (クーロン) (1 Cl = 1 A-s)、長さ (メートル)、速度 (m/s)。

左手の法則を使用してローレンツ力の方向を決定する

マクロオブジェクトの世界では、ローレンツ力はアンペア力として現れるため、左手の法則を使用してその方向を決定できます。

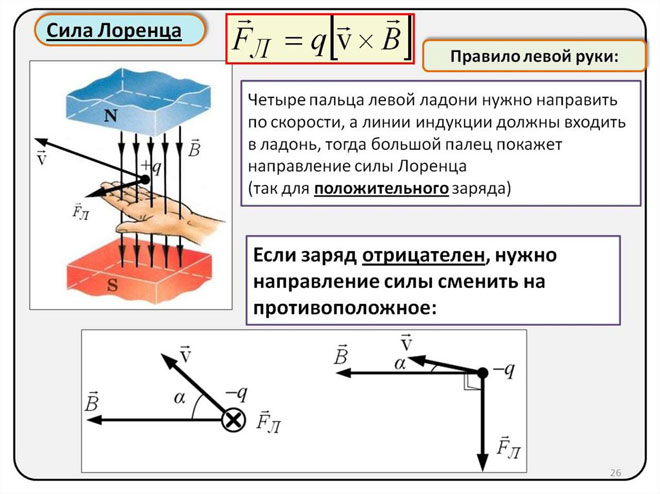
左手の法則を使ってローレンツ力の方向を決定します。

開いた手のひらが磁力線に対して垂直になるように左手を配置すると、4 本の指が電流の方向に伸ばされ、ローレンツ力は親指を曲げる方向に向けられます。、指しています。

磁場中の荷電粒子の動き

最も単純な場合、つまり磁気誘導のベクトルと粒子の速度が直交している場合、速度ベクトルに垂直なローレンツ力はその方向を変えることしかできません。したがって、速度の大きさとエネルギーは変化しません。したがって、ローレンツ力は力学の向心力と同様に作用し、粒子は円運動します。

また読む：キロワットは何ワットですか.

ニュートンIIの法則によると( $F = m\cdot a$ ) 粒子の回転半径を決定できます。

$N = \frac {m\cdot v}{q\cdot B}$ .

粒子の比電荷が変化するにつれて ( $\frac{q}{m}$ )、半径も変化します。

この場合、回転周期 T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ .速度に依存しないので、速度の異なる粒子同士の位置は同じになります。

均一な磁場における荷電粒子の運動。

より複雑なケースでは、粒子の速度と磁場強度の間の角度が任意である場合、粒子はらせん状の軌道に沿って移動します-磁場に平行に向けられた速度成分を犠牲にして徐々に、その影響下で円周に沿って垂直成分。

工学におけるローレンツ力の応用

キネスコープ

最近まで LCD (フラットスクリーン) に取って代わられたキネスコープは、ローレンツ力なしでは機能しませんでした。狭い電子の流れから画面上にテレビ画像を形成するために、偏向コイルを使用して線形に変化する磁場を作成します。ラインコイルは電子ビームを左右に動かし、フレームコイルは垂直方向の動きを担当し、水平に走るビームを上から下に動かします。同じ原理が使用されていますオシロスコープ - 交流電圧の研究用。

質量分析装置

質量分析計は、荷電粒子の回転半径がその特定の電荷に依存することを利用するデバイスです。その動作原理は次のとおりです。

人工的に生成された電場によって加速される荷電粒子の発生源は、空気分子の影響を排除するために真空チャンバー内に配置されます。粒子は光源から飛び出し、円の円弧を通過して写真乾板に当たり、痕跡を残します。特定の電荷に応じて、弾道の半径、つまり着弾点が変化します。この半径は簡単に測定でき、それがわかれば粒子の質量を計算できます。たとえば、質量分析計を使用して、月の土壌の組成を調べました。

また読む：電気に関係する職業を教えてください

サイクロトロン

周期の独立性、したがって磁場の存在下での荷電粒子の速度からの回転周波数は、粒子を高速に加速するように設計されたサイクロトロンと呼ばれる装置で使用されます。サイクロトロンは、2 つの中空の金属半円筒、デュアン (それぞれがラテン文字の D のような形をしています）、まっすぐな面が互いに短い距離で向き合うように配置されます。

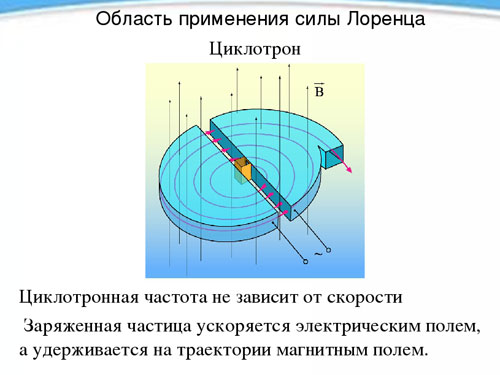
サイクロトロン - ローレンツ力の応用。

デュアントは一定の均一な磁場に置かれ、それらの間に交流電場が作成されます。その周波数は、磁場強度と比電荷によって決定される粒子回転の周波数に等しくなります。回転期間中（あるデュアントから別のデュアントへの移行中）に2回電場にさらされると、粒子はそのたびに加速され、軌道半径が増加し、ある瞬間に必要な速度を得て飛び出します穴を通してデバイス。このようにして、陽子を 20 MeV のエネルギーまで加速することができます。メガエレクトロンボルト).