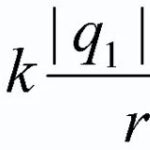電位の概念は、静電気と電気力学の理論の重要な基礎の 1 つです。その本質を理解することは、物理学のこれらのセクションをさらに研究するための前提条件です。
電位とは
単位電荷 q を、静止電荷 Q によって作成された場に置くとします。 クーロン力 F=k*Qq/r.
以下、k=((1/4)*π*ε* ε)、ここで ε0 — は電気定数 (8.85*10-12 F/m)、ε 媒体の誘電率.
に紹介される 充電 この力の作用の下で動くことができ、力は何らかの仕事をします。これは、2 つの電荷のシステムが、両方の電荷の大きさとそれらの間の距離に依存するポテンシャル エネルギーを持ち、このポテンシャル エネルギーの値が電荷 q の大きさに依存しないことを意味します。ここで、電位の定義が導入されます。これは、電場のポテンシャル エネルギーと電荷の大きさの比に等しくなります。
φ=W/q、
ここで、W は電荷系によって生成されるフィールドのポテンシャル エネルギーであり、ポテンシャルはフィールドのエネルギー特性です。電場内で電荷 q をある程度の距離移動させるには、クーロン力に打ち勝つためにいくらかの作業を費やす必要があります。ポイントのポテンシャルは、単位電荷をそのポイントから無限に移動するのに必要な仕事に等しい.注意すべきこと:
- この仕事は、電荷のポテンシャルエネルギーの損失に等しくなります(A = W2-W1);
- 仕事は電荷の軌跡に依存しません。
SI システムでは、電位の単位は 1 ボルトです (ロシア語の文献では V、外国の文献では V で表されます)。 1 V=1J/1 Kl、つまり、1 Kl の電荷を無限遠に移動するのに 1 ジュールの仕事が必要な場合、1 ボルトの点の電位について話すことができます。この名前は、電気工学の発展に多大な貢献をしたイタリアの物理学者アレッサンドロ・ボルタに敬意を表して選ばれました。
電位とは何かを視覚化するために、2 つの物体の温度、または空間の異なる点で測定された温度と比較できます。温度は物体の加熱の尺度であり、電位は電荷の尺度です。一方の物体は他方の物体よりも加熱されていると言われ、一方の物体はより帯電しており、他方の物体は帯電していないとも言えます。これらの体は異なる可能性を秘めています。
ポテンシャルの値は座標系の選択に依存するため、あるレベルをゼロと見なす必要があります。温度を測定する場合、たとえば、氷が溶ける温度を参照境界として使用できます。電位の場合、通常、無限遠点の電位はゼロと見なされますが、問題によっては、アースの電位またはコンデンサのカバーの1つの電位がゼロと見なされる場合があります。
ポテンシャルの性質
ポテンシャルの重要なプロパティには次のものがあります。
- 電場が複数の電荷によって生成される場合、特定の点でのポテンシャルは、各電荷によって生成されるポテンシャルの代数的合計 (電荷の符号を考慮) に等しくなります φ=φ1+φ2+φ3+φ4+φ5+...+φn;
- 電荷からの距離が、電荷自体が点のように考えられるようなものである場合、総ポテンシャルは式 φ=k*(q1/r1+q2/r2+q3/r3+...+qn/rn)、ここで、r は対応する電荷から問題の点までの距離です。
場が電気双極子 (反対の符号の 2 つの接続された電荷) によって形成される場合、双極子から距離 r にある任意の点の電位は φ=k*p*cosά/r に等しくなります。2、 どこ:
- p は双極子の電気アームで、q*l に等しく、l は電荷間の距離です。
- r は双極子までの距離です。
- ά は双極子アームと半径ベクトル r の間の角度です。
ポイントが双極子軸上にある場合、cosά=1 および φ=k*p/r2.
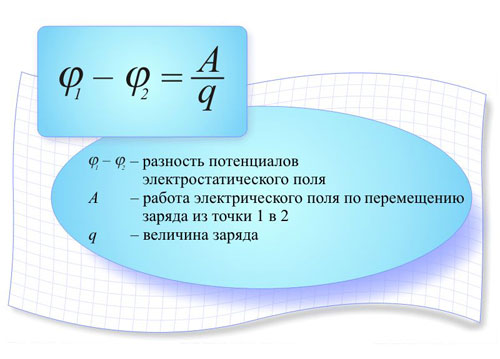
電位差
2 点に一定の電位があり、等しくない場合、2 点間に電位差があるという。ポイント間で電位差が発生します。
- その可能性は、さまざまな兆候の電荷によって決定されます。
- 任意の符号の電荷からのポテンシャルを持つポイントとゼロポテンシャルを持つポイント。
- 等号のポテンシャルを持つが、モジュロが異なる点。
つまり、電位差は座標系の選択に依存しません。ゼロ マーク (海面など) に対して異なる高さに位置する水たまりとの類似性を引き出すことができます。
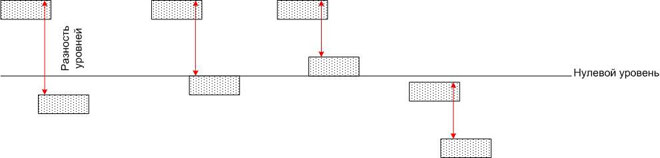
各プールの水には特定のポテンシャルエネルギーがありますが、2つのプールをチューブで接続すると、それぞれに水の流れがあり、その流れはチューブのサイズだけでなく、だけでなく、地球の重力場における位置エネルギーの差 (つまり、高さの差) によっても異なります。この場合、位置エネルギーの絶対値は問題になりません。
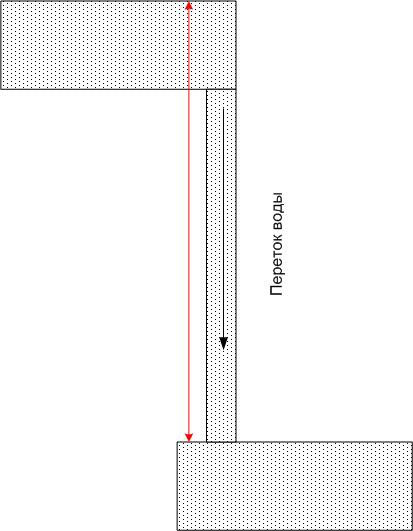
同様に、導体を電位の異なる 2 点に接続すると、 電流導体の抵抗だけでなく、電位差によっても決定されます(絶対値ではありません)。水の例えを続けると、上流の盆地の水はすぐになくなり、水を元に戻す力 (ポンプなど) がなければ、流れはすぐに止まると言えます。
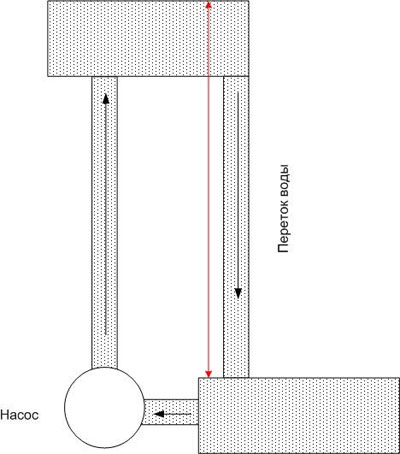
電気回路でも同じです。電位差を一定のレベルに保つには、電荷 (または電荷担体) を電位が最も高い点に移動させる力が必要です。この力は起電力と呼ばれ、EMFと略されます。 EMF は、電気化学、電磁気など、さまざまな性質を持つことができます。
実際には、重要なのは主に、電荷キャリアの軌道の始点と終点の間の電位差です。この場合、この差は電圧と呼ばれ、SIでもボルトで測定されます。電場が 1 クーロンの電荷をある点から別の点に移動する際に 1 ジュールの仕事をする場合、1 ボルトの電圧を表すことができます。つまり、1V=1J/1KL であり、J/KL は潜在的な違い。
等電位面
いくつかの点の電位が同じで、これらの点が面を形成する場合、そのような面は等電位と呼ばれます。たとえば、電荷に外接する球はこの性質を持ちます。これは、電場が距離とともにすべての方向で等しく減少するためです。
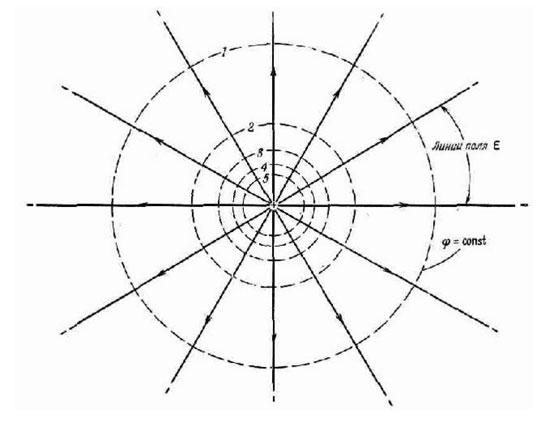
この表面上のすべての点は同じポテンシャル エネルギーを持っているため、そのような球体上で電荷を移動しても仕事は消費されません。いくつかの電荷を持つシステムの等電位面は、より複雑な形状をしていますが、興味深い特性が 1 つあります。それらは決して交差しません。電界の力線は、各点で同じ電位を持つ表面に対して常に垂直です。等電位面を平面で切断すると、等電位線が得られます。等電位面と同じ性質を持っています。実際には、例えば静電場に置かれた導体の表面上の点は、等しい電位を有する。
電位と電位差の概念を理解したら、電気現象をさらに研究し始めることができます。しかし、知識を深めるための基本的な原則と概念を理解することができないため、以前はそうではありませんでした.
関連記事: