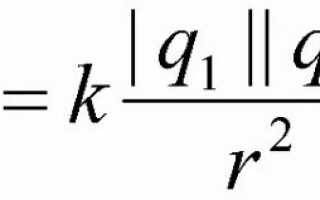荷電体の間には相互作用力があり、それによって互いに引き付けたり反発したりできます。クーロンの法則はこの力を説明し、物体自体のサイズと形状に応じてその影響の程度を示します。この物理法則については、この記事で説明します。
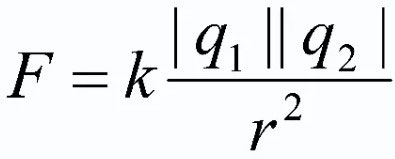
コンテンツ
ステーショナリーポイント料金
クーロンの法則は、サイズが他の物体からの距離よりもはるかに小さい静止物体に適用されます。そのような物体には電荷が集中している点があります。物理的な問題を解決するとき、問題の体のサイズはあまり重要ではないため、無視されます。
実際には、休憩ポイント料金は次のように表されます。
この場合、q1 とq2 - それは ポジティブ これらにはクーロン力が働きます（図には示していません）。ポイント オブジェクトのサイズは問題ではありません。
ノート！ 静止電荷は互いに所定の距離にあり、問題では通常文字rで示されます。さらにこの論文では、これらの電荷を真空で検討します。
シャルル・クーロンのねじりスケール
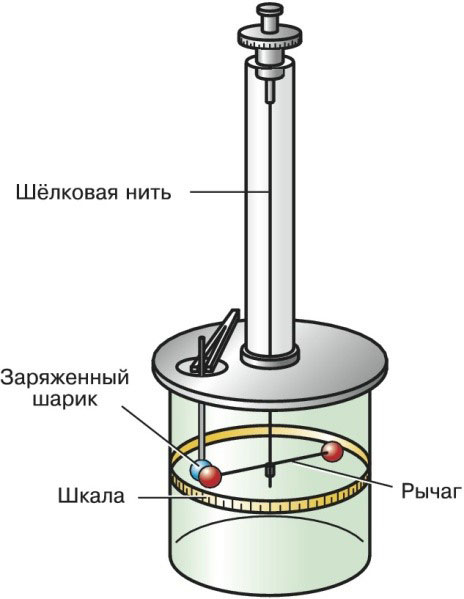
1777 年にクーロンによって開発されたこの装置は、力の依存性を導き出すのに役立ち、後にクーロンにちなんで名付けられました。点電荷と磁極の相互作用を研究するために使用されます。
ねじりスケールには、垂直面に配置された小さな絹の糸があり、その上にバランスのとれたてこがぶら下がっています。レバーの端に点電荷があります。
外力の作用下で、レバーは水平に動き始めます。レバーは、糸の弾性力によってバランスが取れるまで平面内を移動します。
移動の過程で、レバーは垂直軸から一定の角度だけずれます。これを d とし、回転角と呼びます。このパラメータの値がわかれば、発生する力のトルクを見つけることができます。
チャールズ クーロンのねじりスケールは次のようになります。
比例係数kと電気定数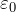 
クーロンの法則式には、パラメータ k、比例係数、または - 電気定数。電気定数 多くの参考書、教科書、インターネットで紹介されており、数える必要はありません。に基づく真空中の比例係数 よく知られている式を使用して見つけることができます。
ここ 
- 電気定数、
- パイ数、
- 真空中の比例係数。
追加情報！ 上記のパラメータを知らなければ、2 点電荷間の相互作用力を見つけることは不可能です。
クーロンの法則の定式化と公式
上記を要約するには、静電気の主な法則の公式な定式化を与える必要があります。次の形式を取ります。
真空中の 2 つの静止点電荷の相互作用力は、これらの電荷の積に正比例し、それらの間の距離の 2 乗に反比例します。 そして、電荷の積はモジュロで取らなければなりません！
この式 q1 とq2 - ポイント料金、考慮される団体です。 r2 - は、これらの物体間の平面上の距離であり、正方形として取得されます。 k は比例係数 (
真空用）。
クーロン力の方向と式のベクトル形式
式を完全に理解するために、クーロンの法則を視覚的に表すことができます。
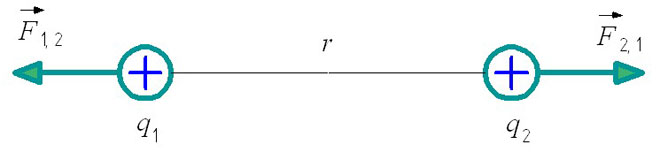
ふ1,2 - は、2 番目の電荷に対する最初の電荷の相互作用力です。
ふ2,1 - は、最初の電荷に対する 2 番目の電荷の相互作用力です。
また、静電気の問題を解決するときは、重要な規則を考慮する必要があります。同じ名前の電荷は反発し、反対の名前の電荷は引き付けます。これにより、図内の相互作用力の位置が決まります。
反対の電荷が考慮される場合、それらの相互作用力は互いの方向に向けられ、それらの引力を表します。
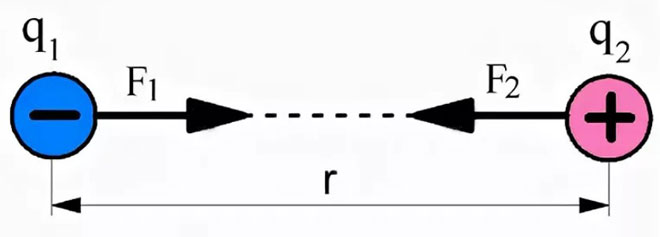
ベクトル形式の静電気の基本法則の式は、次のように表すことができます。
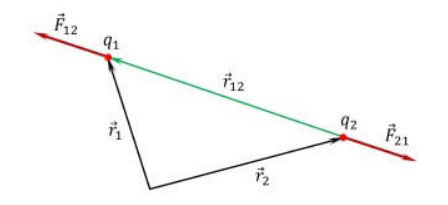
- 電荷q2の側で、点電荷q1に作用する力、
- 電荷q2を電荷q1に接続する半径ベクトル、
重要！ 式をベクトル形式で記述したら、符号を正しく配置するために、2 点電荷の相互作用力を軸に投影する必要があります。このアクションは形式的なものであり、多くの場合、メモなしで精神的に実行されます。
クーロンの法則が実際に適用される場所
静電気の基本法則は、チャールズ クーロンの最も重要な発見であり、多くの分野で応用されています。
有名な物理学者の作品は、さまざまなデバイス、機器、装置を発明する過程で使用されました。たとえば、避雷針。
避雷針を使用して、家や建物は雷雨の際に落雷から保護されます。したがって、電気機器の保護の程度が向上します。
避雷針は次の原理で機能します。雷雨の間、強力な誘導電荷が徐々に地面に蓄積され、上昇して雲に引き寄せられます。これにより、地面にかなりの電界が発生します。避雷針の近くでは電界が強くなり、先端からコロナ電荷が着火します。
次に、地面に形成された電荷は、チャールズ・クーロンの法則に従うべきであるように、反対の符号を持つ雲の電荷に引き寄せられ始めます。すると空気が電離し、避雷針の先端付近では電界強度が低くなります。したがって、落雷が建物に入るリスクは最小限に抑えられます。
ご注意ください！ 避雷針のある建物に衝突しても、火事は発生せず、すべてのエネルギーが地面に流れ込みます。
クーロンの法則に基づいて、「粒子加速器」と呼ばれる装置が開発され、今日大きな需要があります。
このデバイスは強い電場を作り出し、そこに入る粒子のエネルギーを増加させます。
クーロンの法則における力の方向
前述のように、2 点電荷の相互作用力の方向は、それらの極性に依存します。つまり、同じ隣の電荷は反発し、反対の隣の電荷は引き寄せられます。
クーロン力は、半径ベクトルと同じであるため、半径ベクトルとも呼ばれます。それらは、それらの間に引かれた線に沿って向けられます。
いくつかの物理的な問題では、点電荷として捉えることができない複雑な形状の物体があります。つまり、そのサイズを無視することはできません。この状況では、問題の物体をいくつかの小さな部分に分割し、クーロンの法則を適用して各部分を個別に計算する必要があります。
除算で得られた力ベクトルは、代数と幾何学の規則によって合計されます。その結果が結果として生じる力であり、これが問題の答えとなります。この解法は、しばしば三角法と呼ばれます。
法律の発見の歴史
上記の法則による 2 点電荷の相互作用は、1785 年にチャールズ クーロンによって最初に証明されました。物理学者は、ねじりスケールを使用して定式化された法則の真実性を証明することができました。その動作原理も記事に示されています。
クーロンは、球状コンデンサの内部に電荷がないことも証明しました。これが彼が問題の物体間の距離を変えることによって静電気力の大きさを変えることができるという主張に到達した方法です.
このように、クーロンの法則は今でも静電気の最も重要な法則であり、これに基づいて多くの偉大な発見がなされています。この記事では、法律の公式な定式化が提示され、その構成要素が詳細に説明されています。
関連記事：
