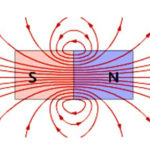
この記事では、誘導 EMF が発生する状況での概念を理解します。また、電場が導体に現れるときの磁束の出現の重要なパラメータとしてインダクタンスを見ていきます。
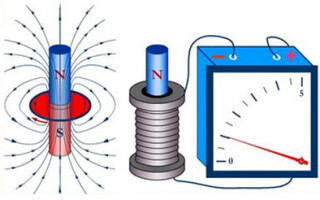
電磁誘導は、時間とともに変化する磁場によって電流が生成されることです。ファラデーとレンツの発見のおかげで、規則性が法則として定式化され、電磁フラックスの理解に対称性が導入されました。マクスウェルの理論は、電流と磁束の知識をまとめました。ヘルツの発見を通じて、人類は電気通信について学びました。
磁束
電流が流れると導体の周りに電磁界が発生しますが、逆の現象である電磁誘導も並行して発生します。例として磁束を考えてみましょう。導体フレームが誘導のある電場に置かれ、磁力線に沿って上から下に、または磁力線に垂直に右から左に移動した場合、フレームを通過する磁束は定値であること。
フレームがその軸を中心に回転すると、しばらくすると磁束が特定の値だけ変化します。その結果、フレームに誘導起電力が発生し、誘導電流と呼ばれる電流が現れます。
誘導起電力
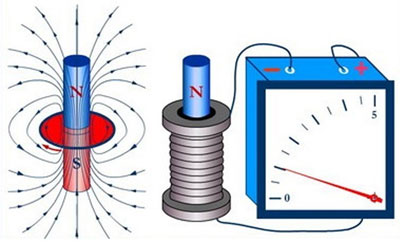
誘導性 EMF の概念が何であるかを詳しく理解しましょう。導体が磁場内に置かれ、磁力線が交差して移動すると、誘導EMFと呼ばれる起電力が導体に現れます。また、導体が静止したままで、磁場が移動して導体と磁力線を横切る場合にも発生します。
EMF が発生する導体が外部回路に近づくと、この EMF の存在により回路に誘導電流が流れ始めます。電磁誘導は、磁力線が導体を横切った瞬間に導体に EMF が誘導される現象を伴います。
電磁誘導は、機械エネルギーを電流に変換する逆のプロセスです。この概念とその法則は電気工学で広く使用されており、ほとんどの電気機械はこの現象に基づいています。
ファラデーとレンツの法則
ファラデーとレンツの法則は、電磁誘導のパターンを表しています。
ファラデーは、磁気効果が磁束の時間変化の結果として現れることを明らかにしました。交流磁流が導体を横切った瞬間、導体に起電力が生じ、電流が発生します。永久磁石も電磁石も電流を発生させることができます。
科学者は、回路を横切る電力線の数が急激に変化すると、電流の強度が増加すると判断しました。つまり、電磁誘導のEMFは、磁束の速度に直接依存したままです。
ファラデーの法則によると、EMF 誘導の式は次のように定義されます。
E = - dF/dt。
「マイナス」記号は、誘導された EMF の極性、磁束方向、および変化する速度の間の関係を示します。
レンツの法則によれば、起電力はその方向によって特徴付けることができます。コイル内の磁束が変化すると誘導起電力が発生し、急速な変化では起電力が増加します。
誘導EMFを備えたコイルが外部回路に短絡すると、誘導電流が流れるため、導体の周りに磁場が現れ、コイルはソレノイドの特性を獲得します。その結果、コイルの周囲に独自の磁場が形成されます。
E. H. レンツは、コイル内の誘導電流の方向と誘導 EMF を決定する法則を確立しました。この法則は、コイル内の誘導のEMFが、コイルの所定の磁束が外部磁束の変化を回避することを可能にする方向の電流をコイルに形成すると述べています。
レンツの法則は、外部磁場を変更する構成や方法に関係なく、導体内の電流誘導のすべての状況に適用されます。
磁場中のワイヤーの動き
誘導 EMF の値は、磁力線が交差する導体の長さによって決まります。力線が増えると、誘導 EMF の値が増加します。磁場と誘導が増加すると、導体内の EMF の値が大きくなります。したがって、磁場内を移動する導体のEMF誘導の値は、磁場誘導、導体の長さ、およびその移動速度に直接依存します。
この依存性は、式 E = Blv に反映されています。ここで、E は誘導の EMF です。 B は磁気誘導の値です。 I は導体の長さです。 v はその移動速度です。
磁場内を移動する導体では、誘導 EMF は磁力線と交差するときにのみ現れることに注意してください。導体が磁力線に沿って移動する場合、EMF は誘導されません。このため、この式は、導体の運動が力線に対して垂直に向けられている場合にのみ適用されます。
誘導されたEMFと導体内の電流の方向は、導体自体の方向によって決まります。方向を明らかにするために、右手の法則が開発されました。磁力線がその方向に入るように右手の手のひらを持ち、親指が導体の運動方向を示す場合、他の 4 本の指は誘導起電力の方向と電流の方向を示します。指揮者。
回転コイル
電流発生器の機能は、特定の巻き数がある磁束内でのコイルの回転に基づいています。 EMF は、式磁束 F = B x S x cos α (磁束が通過する表面積と形成される角度の余弦を乗じた磁気誘導) に基づいて、磁束が交差するときに常に電気回路に誘導されます。方向ベクトルによって、線平面に垂直)。
式によると、F は状況の変化の影響を受けます。
- 磁束が変化すると方向ベクトルが変化します。
- 回路によって囲まれた領域が変化します。
- 角度が変わります。
磁石が静止している場合、または電流が変化していない場合、EMF を誘導することができますが、単にコイルが磁場内でその軸を中心に回転する場合です。この場合、角度の値が変化すると磁束が変化します。コイルが回転すると磁束線と交差し、EMF が発生します。均一な回転では、磁束に周期的な変化があります。また、1 秒ごとに交差する力線の数は、等しい時間間隔で等しくなります。
実際には、オルタネーターでは、コイルは静止したままで、電磁石はコイルの周りを回転します。
自己誘導EMF
交流電流がコイルを通過すると、EMF を誘導する変化する磁束によって特徴付けられる交流磁場が生成されます。この現象は自己誘導と呼ばれます。
磁束は電流の強さに比例するため、自己誘導 EMF の式は次のようになります。
F = L x I、ここで L は Gn で測定されるインダクタンスです。その値は、単位長さあたりの巻き数と断面のサイズによって決まります。
相互誘導
2 つのコイルを隣り合わせに配置すると、相互誘導の EMF が発生します。これは、2 つの回路の構成と相互の向きによって決まります。回路の分離が大きくなると、2 つのコイルに共通の磁束が減少するため、相互インダクタンスの値が減少します。
相互誘導のプロセスを詳しく考えてみましょう。 2 つのコイルがあり、N1 ターンの 1 つのワイヤに沿って電流 I1 が流れ、磁束が生成され、N2 ターン数の 2 番目のコイルを通過します。
最初のコイルに対する 2 番目のコイルの相互インダクタンスの値:
M21 = (N2 × F21)/I1。
磁束の値:
F21 = (M21/N2) × I1。
誘導 EMF は次の式で計算されます。
E2 = - N2 x dF21/dt = - M21x dI1/dt.
最初のコイルでは、誘導 EMF の値は次のとおりです。
E1 = - M12 x dI2/dt。
いずれの場合も、一方のコイルに相互誘導によって誘導される起電力は、もう一方のコイルの電流の変化に正比例することに注意することが重要です。
相互インダクタンスは等しいと見なされます。
M12=M21=M.
結果として、E1 = - M x dI2/dt および E2 = M x dI1/dt となります。 M = K √ (L1 x L2)、ここで、K はインダクタンスの 2 つの値の間の結合係数です。
相互誘導は変圧器で広く使用されており、交流電流の値を変更する可能性があります。このデバイスは、共通のコアに巻かれた一対のコイルです。第 1 コイルの電流は、磁気コアに変化する磁束を形成し、第 2 コイルに電流を形成します。 2 番目のコイルよりも 1 番目のコイルの巻き数が少ないと電圧が上昇し、それに対応して 1 番目のコイルの巻き数が多いと電圧が減少します。
電気エネルギーの生成と変換に加えて、磁気誘導の現象は他のデバイスで使用されます。たとえば、磁気浮上列車では、レール内の電流と直接接触せずに移動しますが、電磁反発のために数センチ高くなります。
関連記事: