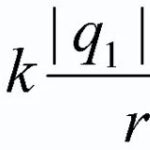Die Lorentzkraft und die Regel der linken Hand. Bewegung von geladenen Teilchen in einem Magnetfeld

Ein Leiter, der sich in einem Magnetfeld befindet Leiterdurch die ein elektrischer Strom fließt einen elektrischen Stromwird von der Ampere-Kraft beeinflusst $F_A$ und seine Größe kann nach folgender Formel berechnet werden

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

wobei $I$ и $l$ - Amperezahl und Länge des Leiters, $B$ - die Induktion des Magnetfeldes, $\alpha$ - der Winkel zwischen den Richtungen des Stroms und der magnetischen Induktion. Warum ist das so?

Lorentz-Kraft. Bewegung eines geladenen Teilchens in einem Magnetfeld.

Inhalt

1 Was ist die Lorentz-Kraft - Definition, wann tritt sie auf, wie lautet die Formel?
2 Bestimmung der Richtung der Lorentzkraft mit Hilfe der Linken-Hand-Regel
3 Bewegung eines geladenen Teilchens in einem Magnetfeld
4 Anwendung der Lorentzkraft in der Technik

Was ist die Lorentz-Kraft - Definition, wann sie auftritt, Ableitung der Formel

Es ist bekannt, dass elektrischer Strom die geordnete Bewegung geladener Teilchen ist. Es ist auch bekannt, dass jedes dieser Teilchen bei seiner Bewegung in einem Magnetfeld einer Kraft ausgesetzt ist. Damit eine Kraft wirken kann, muss ein Teilchen in Bewegung sein.

Die Lorentzkraft ist die Kraft, die auf ein elektrisch geladenes Teilchen wirkt, wenn es sich in einem Magnetfeld bewegt. Seine Richtung ist orthogonal zu der Ebene, in der die Geschwindigkeitsvektoren des Teilchens und die Magnetfeldstärke liegen. Die Lorentz-Kraft ist die Ampere-Kraft. Wenn man sie kennt, kann man die Formel für die Lorentz-Kraft ableiten.

Die Zeit, die ein Teilchen benötigt, um einen Abschnitt eines Leiters zu durchqueren, $t = \frac {l}{v}$ wobei $l$ - ist die Länge des Segments, $v$ - Geschwindigkeit des Teilchens. Die Gesamtladung, die während dieser Zeit über den Querschnitt des Leiters übertragen wird, $Q = I\cdot t$ . Setzt man hier den Wert der Zeit aus der vorherigen Gleichung ein, ergibt sich

$Q = \frac {I\cdot l}{v}$ (2)

Zugleich $F_A = F_L\\cdot N$ wobei $N$ - ist die Anzahl der Teilchen im betrachteten Leiter. Zugleich $N = \frac {Q}{q}$ wobei $q$ - ist die Ladung eines Teilchens. Durch Einsetzen in die Formel $Q$ aus (2) kann man erhalten:

$N = \frac {I\cdot l}{v\cdot q}$

So,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Unter Verwendung von (1) kann der vorherige Ausdruck wie folgt geschrieben werden

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Nach Kürzungen und Übertragungen erhalten wir die Formel zur Berechnung der Lorentzkraft

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Da die Formel für einen Kraftmodul geschrieben ist, sollte sie wie folgt geschrieben werden:

Lesen Sie auch: Wie konvertiert man Ampere in Watt und zurück?

$F_L = |q||\cdot v\cdot B\cdot sin\alpha$ (3)

Seit $sin\alpha = sin(180^{\circ} - \alpha)$ , spielt es für die Berechnung des Lorentz-Moduls keine Rolle, ob die Geschwindigkeit in oder gegen die Stromrichtung verläuft, und man kann sagen, dass $\alpha$ - ist der Winkel, den die Vektoren der Geschwindigkeit des Teilchens und der magnetischen Induktion bilden.

Wenn man die Formel in Vektorform schreibt, sieht sie wie folgt aus:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\mal \vec{B}]$ - ist das Vektorprodukt, das zu einem Vektor mit dem Modulus gleich $v\cdot B\cdot sin\alpha$ .

Aus Formel (3) können wir schließen, dass die Lorentzkraft maximal ist, wenn die Richtungen des elektrischen Stroms und des Magnetfelds senkrecht zueinander stehen, d.h. bei $\alpha = 90^{\circ}$ und verschwinden bei ihrer Parallelität ( $\alpha = 0^{\\\circ}$ ).

Es sei daran erinnert, dass man für eine korrekte quantitative Antwort - z. B. bei der Lösung von Problemen - SI-Einheiten verwenden sollte, bei denen die magnetische Induktion in Tesla gemessen wird (1 Tesla = 1 kg-c⁻²-А⁻¹), Kraft in Newton (1 N = 1 kg-m/s²), Stromstärke in Ampere, Ladung in Coulon (1 Cl = 1 A-s), Länge in Metern, Geschwindigkeit in m/s.

Bestimmung der Richtung der Lorentzkraft mit Hilfe der Linken-Hand-Regel

Da sich die Lorentz-Kraft in der Welt der Makro-Objekte als Ampere-Kraft manifestiert, können wir die Linke-Hand-Regel verwenden, um ihre Richtung zu bestimmen.

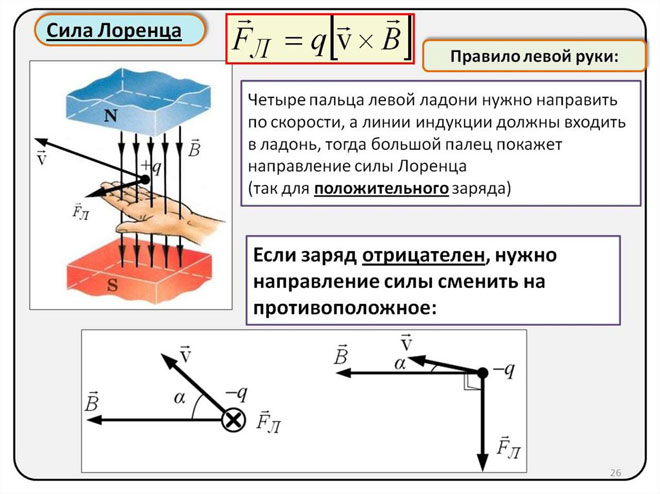
Bestimmung der Richtung der Lorentz-Kraft mit Hilfe der Linken-Hand-Regel.

Wenn die linke Hand senkrecht zu den Magnetfeldlinien steht und auf diese gerichtet ist, sollten die vier Finger in Richtung des Stroms ausgestreckt sein, dann wird die Lorentzkraft dorthin gerichtet, wohin der Daumen, der gebogen sein sollte, zeigt.

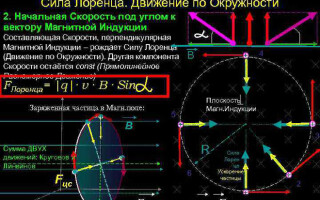
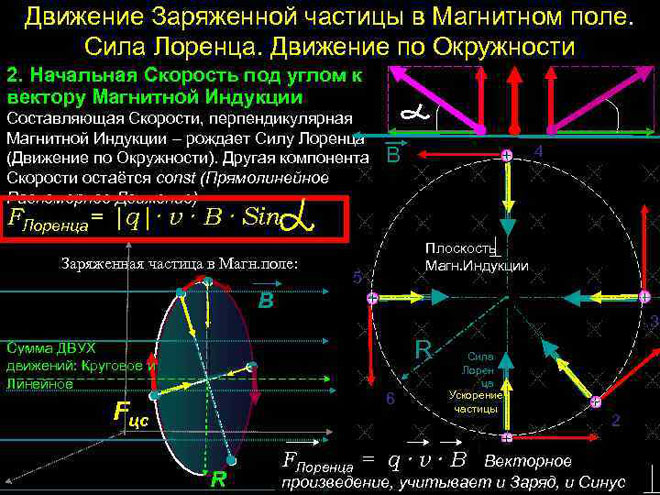
Bewegung eines geladenen Teilchens in einem Magnetfeld

Im einfachsten Fall, d.h. bei Orthogonalität der Vektoren der magnetischen Induktion und der Geschwindigkeit des Teilchens, kann die Lorentzkraft, die senkrecht zum Geschwindigkeitsvektor steht, nur ihre Richtung ändern. Die Größe der Geschwindigkeit, also die Energie, bleibt unverändert. Die Lorentzkraft wirkt also analog zur Zentripetalkraft in der Mechanik, und das Teilchen bewegt sich auf einer Kreisbahn.

Lesen Sie auch: Wie viele Watt sind in einem Kilowatt enthalten?

Nach dem zweiten Newtonschen Gesetz ( $F = m\cdot a$ ) kann man den Rotationsradius eines Teilchens bestimmen:

$N = \frac {m\cdot v}{q\cdot B}$ .

Es ist zu beachten, dass sich die spezifische Ladung des Teilchens ändert ( $\frac {q}{m}$ ) ändert sich auch der Radius.

Somit ist die Rotationsperiode T = . $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Sie hängt nicht von der Geschwindigkeit ab, so dass die gegenseitige Position von Teilchen mit unterschiedlichen Geschwindigkeiten gleich ist.

Die Bewegung eines geladenen Teilchens in einem homogenen Magnetfeld.

In dem komplizierteren Fall, in dem der Winkel zwischen der Geschwindigkeit des Teilchens und der Stärke des Magnetfeldes beliebig ist, bewegt es sich entlang einer spiralförmigen Bahn - progressiv auf Kosten der Geschwindigkeitskomponente, die parallel zum Feld gerichtet ist, und in Umfangsrichtung auf Kosten seiner senkrechten Komponente.

Anwendungen der Lorentzkraft in der Technik

Kinescope

Das Kineskop, das bis vor kurzem, als es durch den LCD (Flachbildschirm) ersetzt wurde, in jedem Fernsehgerät zu finden war, hätte ohne die Lorentzkraft nicht funktionieren können. Um ein Fernsehbild auf dem Bildschirm zu erzeugen, wird ein schmaler Strom von Elektronen durch Ablenkspulen geleitet, die ein linear variierendes Magnetfeld erzeugen. Die Zeilenspulen bewegen den Elektronenstrahl von links nach rechts und zurück, die Rahmenspulen sind für die vertikale Bewegung zuständig und bewegen den laufenden Strahl horizontal von oben nach unten. Dasselbe Prinzip wird angewandt in Oszilloskope - Instrumente zur Untersuchung elektrischer Wechselspannungen.

Massenspektrograph

Ein Massenspektrograph ist ein Instrument, das die Beziehung zwischen dem Rotationsradius eines geladenen Teilchens und seiner spezifischen Ladung nutzt. Seine Funktionsweise ist wie folgt:

Eine Quelle geladener Teilchen, die durch ein künstlich erzeugtes elektrisches Feld an Geschwindigkeit gewinnen, befindet sich in einer Vakuumkammer, um den Einfluss von Luftmolekülen auszuschalten. Die Teilchen fliegen aus der Quelle heraus und treffen in einem Kreisbogen auf eine fotografische Platte, auf der sie Spuren hinterlassen. Je nach spezifischer Ladung ändert sich der Flugbahnradius und damit der Auftreffpunkt. Dieser Radius ist leicht zu messen, und wenn man ihn kennt, kann man die Masse des Teilchens berechnen. Mit Hilfe eines Massenspektrographen wurde zum Beispiel die Zusammensetzung des Mondbodens untersucht.

Lesen Sie auch: Welche Berufe gibt es im Zusammenhang mit Elektrizität?

Zyklotron

Die Unabhängigkeit der Periode und damit der Rotationsfrequenz eines geladenen Teilchens von seiner Geschwindigkeit in Anwesenheit eines Magnetfeldes wird in einem Zyklotron genutzt, um Teilchen auf hohe Geschwindigkeiten zu beschleunigen. Das Zyklotron besteht aus zwei hohlen Metallhalbzylindern, Duanten (jeweils in Form des lateinischen Buchstabens D), die sich mit ihren geraden Seiten in geringem Abstand gegenüberstehen.

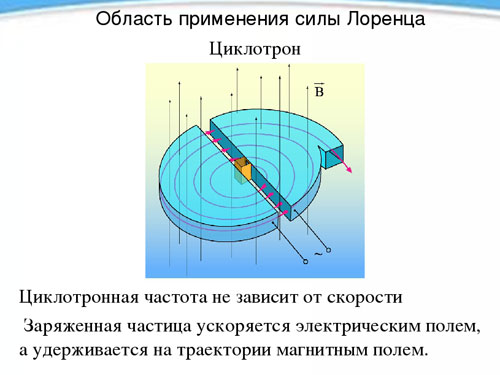
Zyklotron - Anwendung der Lorentz-Kraft.

Die Duanten befinden sich in einem konstanten homogenen Magnetfeld, und zwischen ihnen wird ein elektrisches Wechselfeld erzeugt, dessen Frequenz gleich der Rotationsfrequenz des Teilchens ist, die durch die Stärke des Magnetfelds und die spezifische Ladung bestimmt wird. Da das Teilchen während der Rotationsperiode zweimal vom elektrischen Feld beeinflusst wird (beim Übergang von einem Duant zum anderen), wird es jedes Mal beschleunigt, wodurch sich der Radius der Flugbahn vergrößert, und zu einem bestimmten Zeitpunkt, wenn es die erforderliche Geschwindigkeit erreicht hat, fliegt es durch das Loch aus dem Gerät. Auf diese Weise kann man ein Proton auf eine Energie von 20 MeV beschleunigenMegaelektronenvolt).

Magnetron

Ein so genanntes Magnetron, das in jedem Haus installiert ist Mikrowellenherdist ein weiteres Beispiel für ein Gerät, das mit Hilfe der Lorentz-Kraft funktioniert. Das Magnetron erzeugt ein starkes Mikrowellenfeld, das den Innenraum des Ofens, in dem sich die Speisen befinden, erwärmt. Die Magnete im Magnetron steuern den Weg der Elektronen im Ofen.

Das Magnetfeld der Erde

In der Natur ist die Lorentz-Kraft für den Menschen sehr wichtig. Sein Vorhandensein ermöglicht es dem Magnetfeld der Erde, die Menschen vor der tödlichen ionisierenden Strahlung des Weltraums zu schützen. Das Feld verhindert, dass geladene Teilchen die Planetenoberfläche bombardieren und zwingt sie, ihre Richtung zu ändern.