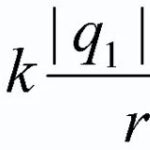Ladungen interagieren in verschiedenen Medien mit unterschiedlichen Stärken miteinander, die durch das Coulomb-Gesetz geregelt werden. Eine Größe namens Dielektrizitätskonstante bestimmt die Eigenschaften dieser Medien.

Inhalt
- 1 Wie hoch ist die Dielektrizitätskonstante?
- 2 Die Natur der Dielektrizitätskonstante
- 3 Dielektrizitätskonstante von verschiedenen Stoffen
- 4 Dielektrizitätskonstante und Kapazität eines Kondensators
- 5 Dielektrische Permittivität und dielektrische Verluste
- 6 Die Abhängigkeit der Dielektrizitätskonstante von äußeren Faktoren
Was ist die dielektrische Permittivität
Nach Angaben von Coulombsches Gesetzgibt es zwei punktförmig stationäre Ladungen q1 und q2 in einem Vakuum mit der Kraft, die durch die Formel Fcl= ((1/4)*π* ε)*(|q1|*|q2|/r2), wobei:
- Fcl - ist die Coulomb-Kraft, N;
- q1, q2 - Module der Ladungen, kl;
- r ist der Abstand zwischen den Ladungen, m;
- ε0 - elektrische Konstante, 8,85*10-12 F/m (Farad pro Meter).
Findet die Wechselwirkung nicht im Vakuum statt, enthält die Formel eine weitere Größe, die die Wirkung der Substanz auf die Coulomb-Kraft bestimmt, und die Notation des Coulomb-Gesetzes sieht wie folgt aus
F=((1/4)*π* ε* ε)*(|q1|*|q2|/r2).
Diese Größe wird mit dem griechischen Buchstaben ε (Epsilon) bezeichnet und ist dimensionslos (hat keine Maßeinheit). Die Dielektrizitätskonstante ist der Dämpfungskoeffizient für die Wechselwirkung von Ladungen in Materie.
In der Physik wird die Dielektrizitätskonstante häufig in Verbindung mit der elektrischen Konstante verwendet. In diesem Fall ist es sinnvoll, den Begriff der absoluten Dielektrizitätskonstante einzuführen. Dies wird mit ε bezeichneta und ist gleich εa= ε* ε. In diesem Fall liegt die absolute Permeabilität in der Dimension F/m. Die normale Permeabilität ε wird auch als relative Permeabilität bezeichnet, um sie von εa.
Die Art der Dielektrizitätskonstante
Die dielektrische Dielektrizitätskonstante beruht auf dem Phänomen der Polarisation unter Einwirkung eines elektrischen Feldes. Die meisten Stoffe sind im Allgemeinen elektrisch neutral, obwohl sie geladene Teilchen enthalten. Diese Teilchen sind chaotisch in einer Materiemasse angeordnet und ihre elektrischen Felder neutralisieren sich im Durchschnitt gegenseitig.
Dielektrika enthalten meist gebundene Ladungen (Dipole genannt). Bei diesen Dipolen handelt es sich in der Regel um Bündel aus zwei ungleichen Teilchen, die spontan entlang der Dicke des Dielektrikums ausgerichtet sind und im Durchschnitt eine elektrische Feldstärke von Null erzeugen. Unter der Einwirkung eines äußeren Feldes neigen die Dipole dazu, sich entsprechend der angelegten Kraft auszurichten. Dadurch entsteht ein zusätzliches elektrisches Feld. Ähnliche Phänomene treten bei unpolaren Dielektrika auf.
Leiter funktionieren auf ähnliche Weise, haben aber freie Ladungen, die durch ein äußeres Feld getrennt sind und ihr eigenes elektrisches Feld erzeugen können. Dieses Feld ist gegen das äußere Feld gerichtet, schirmt die Ladungen ab und verringert die Kraft ihrer Wechselwirkung. Je größer die Polarisationsfähigkeit einer Substanz ist, desto höher ist ε.
Dielektrizitätskonstante verschiedener Stoffe
Verschiedene Stoffe haben unterschiedliche dielektrische Permittivitäten. Der Wert von ε für einige von ihnen ist in Tabelle 1 aufgeführt. Offensichtlich sind diese Werte größer als eins, so dass die Wechselwirkung der Ladungen im Vergleich zum Vakuum immer abnimmt. Es ist auch zu beachten, dass für Luft ε ein wenig mehr als eins ist, deshalb unterscheidet sich die Wechselwirkung der Ladungen in Luft praktisch nicht von der Wechselwirkung im Vakuum.
Tabelle 1. Werte der elektrischen Durchlässigkeit für verschiedene Stoffe.
| Substanz | Dielektrizitätskonstante |
|---|---|
| Bakelit | 4,5 |
| Papier | 2,0..3,5 |
| Wasser | 81 (bei +20°C) |
| Luft | 1,0002 |
| Germanium | 16 |
| Gethinax | 5..6 |
| Holz | 2.7..7.5 (verschiedene Klassen) |
| Keramik Funkkeramik | 10..200 |
| Glimmer | 5,7..11,5 |
| Glas | 7 |
| Textolite | 7,5 |
| Polystyrol | 2,5 |
| Polyvinylchlorid | 3 |
| Fluorkunststoff | 2,1 |
| Bernstein | 2,7 |
Dielektrizitätskonstante und Kapazität eines Kondensators
Die Kenntnis des Wertes von ε ist in der Praxis wichtig, z. B. bei der Auslegung von elektrischen Kondensatoren. Ihre Kapazität ist abhängig von den geometrischen Abmessungen der Einsätze, dem Abstand zwischen ihnen und der Dielektrizitätskonstante des Dielektrikums.
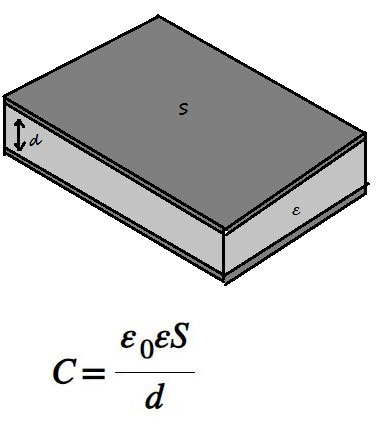
Wenn Sie einen Kondensator herstellen wollen einen Kondensator Wenn die Elektroden eine höhere Kapazität haben, dann vergrößert sich die Fläche der Abdeckungen. Auch die Verringerung des Abstands zwischen den Elektroden stößt auf praktische Grenzen. In diesem Fall kann die Verwendung eines Isolators mit erhöhter Dielektrizitätskonstante helfen. Wenn ein Material mit einem höheren ε verwendet wird, kann die Größe der Elektroden verkleinert oder der Abstand zwischen den Elektroden vergrößert werden, ohne dass es zu einem Verlust kommt. elektrische Kapazität.
Eine andere Kategorie von Materialien ist die der Ferroelektrika, die unter bestimmten Bedingungen eine spontane Polarisation aufweisen können. Sie zeichnen sich in dem hier betrachteten Bereich durch zwei Dinge aus:
- große Werte der Dielektrizitätskonstante (typische Werte reichen von Hunderten bis zu mehreren Tausend);
- die Fähigkeit, den Wert der Dielektrizitätskonstante durch Änderung des äußeren elektrischen Feldes zu steuern.
Diese Eigenschaften werden genutzt, um Kondensatoren mit hoher Kapazität (durch Erhöhung der Dielektrizitätskonstante des Isolators) und geringen Abmessungen herzustellen.
Diese Geräte funktionieren nur in niederfrequenten Wechselstromkreisen - mit steigender Frequenz sinkt ihre Dielektrizitätskonstante. Eine weitere Anwendung von segmentierten Dielektrika sind variable Kondensatoren, deren Eigenschaften sich unter dem Einfluss eines angelegten elektrischen Feldes mit variierenden Parametern ändern.
Dielektrische Permittivität und dielektrische Verluste
Dielektrische Verluste, also der Teil der Energie, der im Dielektrikum als Wärme verloren geht, hängen ebenfalls von der Dielektrizitätskonstante ab. Der Parameter tg δ, der Tangens des Winkels des dielektrischen Verlustes, wird üblicherweise zur Beschreibung dieser Verluste verwendet. Sie charakterisiert die Stärke der dielektrischen Verluste in einem Kondensator, bei dem das Dielektrikum aus einem Material mit einer verfügbaren tg δ besteht. Und die spezifische Verlustleistung für jeden Stoff wird durch die Formel p=E definiert2*ώ*ε*ε*tg δ, wobei
- p ist die spezifische Verlustleistung W;
- ώ=2*π*f - Kreisfrequenz des elektrischen Feldes;
- E - elektrische Feldstärke, V/m.
Es liegt auf der Hand, dass die Verluste im Dielektrikum umso höher sind, je höher die Dielektrizitätskonstante ist, sofern alle anderen Faktoren gleich bleiben.
Abhängigkeit der Dielektrizitätskonstante von äußeren Faktoren
Es ist zu beachten, dass der Wert der Dielektrizitätskonstante von der Frequenz des elektrischen Feldes abhängt (in diesem Fall von der Frequenz der an den Streifen angelegten Spannung). Mit zunehmender Häufigkeit sinkt der Wert von ε für viele Stoffe. Dieser Effekt ist bei polaren Dielektrika besonders ausgeprägt. Dieses Phänomen lässt sich dadurch erklären, dass die Ladungen (Dipole) keine Zeit mehr haben, dem Feld zu folgen. Bei Substanzen, die durch ionische oder elektronische Polarisation gekennzeichnet sind, ist die Frequenzabhängigkeit der Dielektrizitätskonstante gering.
Aus diesem Grund ist die Auswahl der Materialien für das Dielektrikum eines Kondensators so wichtig. Was bei niedrigen Frequenzen funktioniert, führt nicht unbedingt zu einer guten Isolierung bei hohen Frequenzen. Meistens werden unpolare Dielektrika als Isolatoren bei hohen Frequenzen verwendet.
Die Dielektrizitätskonstante ist auch temperaturabhängig und variiert von Stoff zu Stoff. Bei unpolaren Dielektrika sinkt sie mit steigender Temperatur. In diesem Fall spricht man von einem negativen Temperaturkoeffizienten der Kapazität (TKE) für Kondensatoren, die mit einem solchen Isolator hergestellt werden Die Kapazität fällt mit steigender Temperatur nach ε. Bei anderen Stoffen nimmt die Permeabilität mit steigender Temperatur zu, und es können Kondensatoren mit einem positiven TKE erhalten werden. Durch die Paarung von Kondensatoren mit entgegengesetzten TKEs kann eine thermostabile Kapazität erzielt werden.
Das Verständnis und die Kenntnis der Dielektrizitätskonstante verschiedener Stoffe ist für praktische Zwecke wichtig. Und die Möglichkeit, die Höhe der Dielektrizitätskonstante zu steuern, bietet zusätzliche technische Perspektiven.
Ähnliche Artikel: