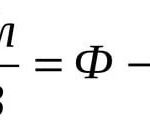Die elektrische Kapazität ist einer der Grundbegriffe der Elektrostatik. Dieser Begriff bezieht sich auf seine Fähigkeit, elektrische Ladung zu speichern. Man kann von der Kapazität eines einzelnen Leiters sprechen oder von der Kapazität eines Systems aus zwei oder mehr Leitern. Die beteiligten physikalischen Prozesse sind ähnlich.

Inhalt
Grundlegende kapazitätsbezogene Konzepte
Wenn ein Leiter eine Ladung q erhalten hat, entsteht an ihm ein Potential φ. Dieses Potenzial hängt von der Geometrie und der Umgebung ab - bei verschiedenen Leitern und Bedingungen verursacht dieselbe Ladung ein anderes Potenzial. Aber φ ist immer proportional zu q:
φ=Cq
Der Koeffizient C und wird als die elektrische Kapazität bezeichnet. Handelt es sich um ein System mit mehreren Leitern (in der Regel zwei), so entsteht eine Potenzialdifferenz oder Spannung U, wenn ein Leiter (der Mantel) aufgeladen wird:
U=Cq, also C=U/q
Die Kapazität kann als das Verhältnis zwischen der Potenzialdifferenz und der daraus resultierenden Ladung definiert werden. Die Maßeinheit für die Kapazität im SI ist das Farad (früher Farad genannt). 1 F = 1 V/1k. Die Kapazität von 1 Farad ist ein System, in dem die Abgabe einer Ladung von 1 Coulomb zu einer Potentialdifferenz von 1 Volt führt. 1 Farad ist ein sehr großer Wert. In der Praxis werden meist Bruchwerte - Picofarad, Nanofarad, Mikrofarad - verwendet.
In der Praxis führt diese Kombination zu einer Batterie, die einer höheren dielektrischen Durchbruchspannung standhält als eine einzelne Zelle.
Berechnung der Kondensatorkapazität
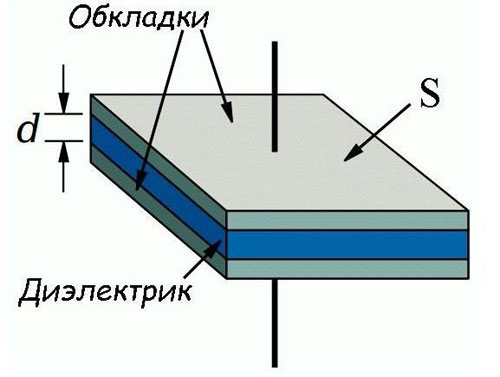
Die in der Praxis am häufigsten verwendeten Elemente mit einer Nennkapazität sind KondensatorenKondensatoren, die aus zwei flachen Leitern (Klemmen) bestehen, die durch ein Dielektrikum getrennt sind. Die Formel zur Berechnung der elektrischen Kapazität eines solchen Kondensators lautet wie folgt:
C=(S/d)*ε*ε0
wo:
- C ist die Kapazität, F;
- S ist die Fläche der Einsätze in Quadratmetern;
- d ist der Abstand zwischen den Deckeln, m;
- ε0 - elektrische Konstante, konstant, 8,854*10−12 W/m;
- ε - Dielektrizitätskonstante, dimensionsloser Wert.
Daraus ist leicht zu erkennen, dass die Kapazität direkt proportional zur Fläche der Abdeckungen und umgekehrt proportional zum Abstand zwischen den Leitern ist. Die Kapazität wird auch durch das Material beeinflusst, mit dem die Abdeckungen getrennt sind.
Um zu verstehen, wie sich die Größen, die die Kapazität bestimmen, auf die Fähigkeit eines Kondensators auswirken, Ladung zu speichern, können Sie ein Gedankenexperiment durchführen, um einen Kondensator mit der höchstmöglichen Kapazität zu erzeugen.
- Sie könnten versuchen, die Fläche der Wicklungen zu vergrößern. Dies würde zu einer drastischen Zunahme von Größe und Gewicht des Geräts führen. Um die Größe der Schichten mit dem sie trennenden Dielektrikum zu verringern, werden die Schichten aufgerollt (zu einem Rohr, flachen Brikett usw.).
- Eine andere Möglichkeit besteht darin, den Abstand zwischen den Einsätzen zu verringern. Es ist nicht immer möglich, die Leiter sehr eng zu positionieren, da die dielektrische Schicht einen gewissen Potenzialunterschied zwischen den Wicklungen aushalten muss. Je geringer die Dicke ist, desto geringer ist die elektrische Festigkeit des Isolierspalts. Wenn Sie diesen Weg einschlagen, erreichen Sie einen Punkt, an dem der Kondensator in der Praxis bedeutungslos wird - er kann nur bei sehr niedrigen Spannungen arbeiten.
- Erhöhung der dielektrischen elektrischen Permeabilität. Dieser Weg hängt von der aktuellen Produktionstechnologie ab. Das Isoliermaterial muss nicht nur einen hohen Permeabilitätswert aufweisen, sondern auch gute dielektrische Eigenschaften besitzen und seine Parameter im erforderlichen Frequenzbereich beibehalten (mit steigender Betriebsfrequenz des Kondensators nehmen die dielektrischen Eigenschaften ab).
Kugelförmige oder zylindrische Kondensatoren können in einigen Spezial- oder Forschungsanwendungen verwendet werden.
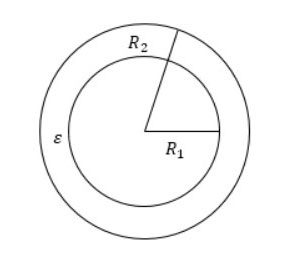
Die Kapazität eines kugelförmigen Kondensators kann nach folgender Formel berechnet werden
C=4*π*ε0 *R1R2/(R2-R1)
wobei R der Radius der Kugeln und π=3,14 ist.
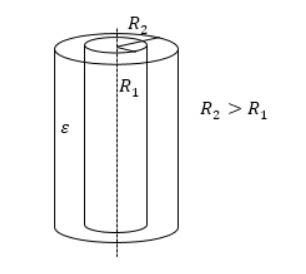
Für einen zylindrischen Kondensator wird die Kapazität wie folgt berechnet:
C=2*π*ε*ε0 *l/ln(R2/R1)
l ist die Höhe der Zylinder, und R1 und R2 sind ihre Radien.
Im Prinzip unterscheiden sich beide Formeln nicht von der Formel für einen Flachkondensator. Die Kapazität wird immer von den linearen Abmessungen der Anschlüsse, dem Abstand zwischen ihnen und den Eigenschaften des Dielektrikums bestimmt.
Verschaltung von Kondensatoren in Reihe und parallel
Kondensatoren können in Reihe geschaltet werden in Reihe oder parallel, wodurch ein Set mit neuen Merkmalen entsteht.
Parallelschaltung
Wenn die Kondensatoren parallel geschaltet sind, ist die Gesamtkapazität der resultierenden Batterie gleich der Summe der Kapazitäten aller ihrer Komponenten. Wenn eine Batterie aus der gleichen Konstruktion von Kondensatoren besteht, kann man sich das so vorstellen, dass die Fläche aller Platten addiert wird. In diesem Fall ist die Spannung an jedem Element der Batterie gleich und die Ladungen addieren sich. Für drei parallel geschaltete Kondensatoren:
- U=U1=U2=U3;
- q=q1+q2+q3;
- C=C1+C2+C3.
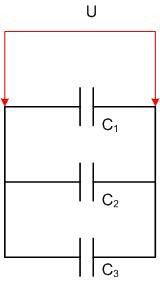
Anschluss in Reihe
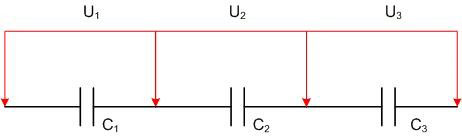
Bei einer Reihenschaltung sind die Ladungen der einzelnen Kapazitäten gleich groß:
q1=q2=q3=q
Die Gesamtspannung verteilt sich im Verhältnis zu Kapazität von Kondensatoren:
- U1=q/ C1;
- U2=q/ C2;
- U3= q/ C3.
Wenn alle Kondensatoren gleich groß sind, fällt an jedem die gleiche Spannung an. Die Gesamtkapazität wird wie folgt berechnet:
C=q/( U1+U2+U3), also 1/C=( U1+U2+U3)/q=1/C1+1/С2+1/С3.
Anwendungen von Kondensatoren in der Technik
Es ist logisch, Kondensatoren als elektrische Energiespeicher zu verwenden. Als solche können sie nicht mit elektrochemischen Quellen (galvanische Batterien, Kondensatoren) konkurrieren, da ihre Energiespeicherkapazität gering ist und sie sich aufgrund von Ladungsverlusten durch das Dielektrikum relativ schnell selbst entladen. Aber ihre Fähigkeit, Energie über einen langen Zeitraum zu speichern und sie dann fast sofort wieder abzugeben, wird häufig genutzt. Diese Eigenschaft wird in Blitzlampen für die Fotografie oder in Lampen für die Anregung von Lasern genutzt.
Kondensatoren sind in der Funktechnik und Elektronik weit verbreitet. Kondensatoren werden in Resonanzkreisen als eines der frequenzerhaltenden Elemente von Schaltkreisen verwendet (das andere Element ist die Induktivität). Die Fähigkeit von Kondensatoren, Gleichstrom zurückzuhalten, ohne den Wechselstromanteil zu verzögern, wird ebenfalls genutzt. Eine solche Verwendung ist bei der Aufteilung von Verstärkerstufen üblich, um den Einfluss der Gleichstrommoden der einen Stufe auf die andere zu eliminieren. Kondensatoren mit hoher Kapazität werden als Glättungsfilter in Stromversorgungen eingesetzt. Darüber hinaus gibt es eine Vielzahl weiterer Anwendungen, bei denen sich die Eigenschaften der Kondensatoren als nützlich erweisen.
Einige praktische Kondensatorentwürfe
In der Praxis wird eine Vielzahl von Flachkondensatoren verwendet. Die Konstruktion des Geräts bestimmt seine Eigenschaften und seinen Anwendungsbereich.
Variabler Kondensator
Ein üblicher Drehkondensator (VAC) besteht aus einer Reihe beweglicher und fester Platten, die durch Luft oder einen festen Isolator getrennt sind. Die beweglichen Platten drehen sich um eine Achse und vergrößern oder verkleinern die Überlappungsfläche. Wenn die bewegliche Einheit zurückgezogen wird, bleibt der Elektrodenabstand unverändert, aber der durchschnittliche Abstand zwischen den Platten vergrößert sich ebenfalls. Die Dielektrizitätskonstante des Isolators bleibt ebenfalls unverändert. Die Kapazität wird durch Veränderung der Fläche der Abdeckungen und des durchschnittlichen Abstands zwischen ihnen eingestellt.

Oxidkondensator
In der Vergangenheit wurde diese Art von Kondensator als Elektrolytkondensator bezeichnet. Es besteht aus zwei Folienstreifen, die durch ein in Elektrolyt getränktes Papierdielektrikum getrennt sind. Der erste Streifen dient als eine Hülle und der zweite Streifen als Elektrolyt. Das Dielektrikum besteht aus einer dünnen Oxidschicht auf einem der Metallstreifen, und der zweite Streifen dient als Stromabnehmer.
Da die Oxidschicht sehr dünn ist und der Elektrolyt in ihrer Nähe liegt, ist es möglich, eine ausreichend hohe Kapazität bei moderater Größe zu erreichen. Der Preis dafür ist die niedrige Betriebsspannung - die Oxidschicht hat keine hohe Durchschlagsfestigkeit. Steigt die Betriebsspannung, muss die Größe des Kondensators erheblich zunehmen.
Ein weiteres Problem besteht darin, dass das Oxid nur in eine Richtung leitfähig ist, so dass solche Kondensatoren nur in Gleichstromkreisen in Bezug auf die Polarität verwendet werden können.
Ionistor
Wie oben gezeigt, sind die traditionellen Methoden zur Steigerung Kondensatoren haben natürliche Grenzen. Der eigentliche Durchbruch war also die Entwicklung des Ionistors.
Obwohl dieses Gerät als Zwischenprodukt zwischen einem Kondensator und einer Batterie betrachtet wird, handelt es sich im Wesentlichen um einen Kondensator.
Der Abstand zwischen den Elektroden wird durch die Verwendung einer elektrischen Doppelschicht drastisch verringert. Die Schichten bestehen aus Ionen, die eine entgegengesetzte Ladung haben. Ein hochporöser Schaumstoff ermöglicht es, die Oberfläche der Schichten drastisch zu vergrößern. Das Ergebnis sind Superkondensatoren mit Kapazitäten von bis zu Hunderten von Farad. Das Problem dieser Geräte ist die niedrige Betriebsspannung (meist im Bereich von 10 Volt).
Die technische Entwicklung ging weiter: In vielen Anwendungen wurden Lampen durch bipolare Transistoren ersetzt, die wiederum durch unipolare Trioden abgelöst wurden. Bei der Schaltungsentwicklung wird auf Induktivitäten so weit wie möglich verzichtet. Und Kondensatoren geben ihre Position auch im zweiten Jahrhundert nicht auf, ihr Design hat sich seit der Erfindung des Leidener Gefäßes nicht grundlegend geändert, und ein Ende ihrer Karriere ist nicht in Sicht.
Ähnliche Artikel: