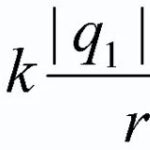Lorentzkracht en de regel van de linkerhand. Beweging van geladen deeltjes in een magnetisch veld

Een geleider geplaatst in een magnetisch veld geleiderwaardoor een elektrische stroom een elektrische stroomwordt beïnvloed door de Ampere kracht $F_A$ en de grootte ervan kan worden berekend met de volgende formule

$F_A=B I I sin$ (1)

waarbij $I$ и $l$ - stroomsterkte en lengte van de geleider, $B$ - de inductie van het magnetisch veld, $\Alfa.$ - de hoek tussen de richtingen van de stroom en de magnetische inductie. Waarom gebeurt dit dan?

Lorentzkracht. Beweging van een geladen deeltje in een magnetisch veld.

Inhoud

1 Wat is de Lorentzkracht - definitie, wanneer het optreedt, het krijgen van de formule
2 Bepaling van de richting van de lorentzkracht met behulp van de linkerhandregel
3 Beweging van een geladen deeltje in een magnetisch veld
4 Toepassing van de lorentzkracht in de techniek

Wat is de Lorentzkracht - definitie, wanneer hij ontstaat, afleiden van de formule

Het is bekend dat elektrische stroom de geordende beweging van geladen deeltjes is. Het is ook bekend dat wanneer deze deeltjes zich in een magnetisch veld bewegen, er op elk van hen een kracht wordt uitgeoefend. Om een kracht te kunnen uitoefenen, moet een deeltje in beweging zijn.

De lorentzkracht is de kracht die op een elektrisch geladen deeltje werkt als het zich in een magnetisch veld beweegt. De richting ervan staat loodrecht op het vlak waarin de snelheidsvectoren van het deeltje en de magnetische veldsterkte liggen. De Lorentz-kracht is de Ampere-kracht. Nu we die kennen, kan de formule voor de lorentzkracht worden afgeleid.

De tijd die een deeltje nodig heeft om een doorsnede van een geleider te doorlopen, $t = \frac {l}{v}$ waarbij $l$ - is de lengte van het segment, $v$ - snelheid van het deeltje. De totale lading die gedurende deze tijd over de doorsnede van de geleider wordt vervoerd, $Q = Icdot t$ . Als we hier de waarde van de tijd uit de vorige vergelijking invullen, hebben we

$Q = \frac {I\cdot l}{v}$ (2)

Tezelfdertijd $F_A = F_Lcdot N$ waarbij $N$ - het aantal deeltjes in de beschouwde geleider is. Tezelfdertijd $N = \frac {Q}{q}$ waarbij $q$ - is de lading van een deeltje. Door substitutie in formule $Q$ uit (2), kan men verkrijgen:

$N = \frac {Ik}{v\cdot q}$

Zo,

$F_A=F_L_Lcdot \frac {I_L}{v\cdot q}$

Met behulp van (1) kan de vorige uitdrukking worden geschreven als

$B$

Na knippen en overbrengen krijgen we de formule voor de berekening van de Lorentzkracht

$F_L = q$

Aangezien de formule is geschreven voor een krachtsmodulus, moet deze als volgt worden geschreven:

Lees ook: Hoe zet je ampère om in watt en terug?

$F_L =q| v v B sinalfa$ (3)

Sinds $sinalfa = sin(180^circ} - \alpha)$ , maakt het voor de berekening van de Lorentz-modulus niet uit of de snelheid in de richting van de stroom is of ertegenin, en kunnen we zeggen dat $\Alfa.$ - is de hoek gevormd door de snelheidsvectoren van het deeltje en de magnetische inductie.

Als je de formule in vectorvorm schrijft, ziet het er zo uit:

$\duiv{v} maal duiv{b}]$

$[\vec{v}]$ - is het vectorproduct dat resulteert in een vector met een modulus gelijk aan $v\cotte B\cotte sinalfa$ .

Uit formule (3) kunnen we concluderen dat de lorentzkracht maximaal is in het geval van loodrechtheid van richtingen van elektrische stroom en magnetisch veld, d.w.z. bij $\Alfa = 90.$ en zullen verdwijnen bij hun parallellisme ( $\Alfa = 0.$ ).

Er zij aan herinnerd dat voor een correct kwantitatief antwoord - bijvoorbeeld bij het oplossen van problemen - gebruik moet worden gemaakt van SI-eenheden, waarin de magnetische inductie wordt gemeten in teslas (1 Tesla = 1 kg-c⁻²-А⁻¹), kracht in newton (1 N = 1 kg-m/s²), stroom in ampère, lading in coulon (1 Cl = 1 A-s), lengte in meter, snelheid in m/s.

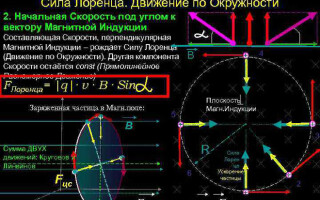
Bepaling van de richting van de Lorentzkracht met behulp van de linkerhandregel

Aangezien in de wereld van macro-objecten de Lorentz-kracht zich manifesteert als een Ampere-kracht, kunnen wij de linkerhandregel gebruiken om de richting ervan te vinden.

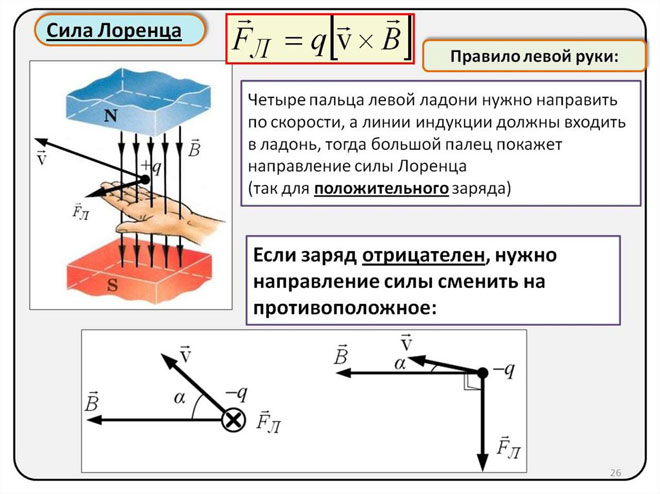
Bepaling van de richting van de Lorentzkracht met behulp van de linkerhandregel.

Met de linkerhand loodrecht op en gericht naar de magnetische veldlijnen, moeten de vier vingers worden uitgestrekt in de richting van de stroom, dan zal de lorentzkracht worden gericht naar waar de duim, die gebogen moet zijn, wijst.

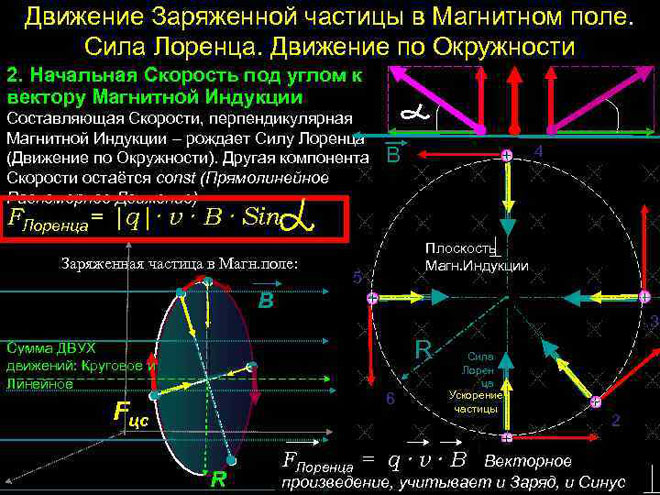
Beweging van een geladen deeltje in een magnetisch veld

In het eenvoudigste geval, d.w.z. met orthogonaliteit van de vectoren van magnetische inductie en snelheid van het deeltje, kan de Lorentz-kracht, die loodrecht staat op de snelheidsvector, alleen zijn richting veranderen. De grootte van de snelheid, dus de energie, zal onveranderd blijven. De lorentzkracht werkt dus analoog aan de centripetale kracht in de mechanica, en het deeltje beweegt in een cirkel.

Lees ook: Hoeveel watt zit er in een kilowatt?

Volgens de tweede wet van Newton ( $F = mcdot a$ ) kan men de draaicirkel van een deeltje bepalen:

$N = \frac {m\cdot v}{q\cdot B}$ .

Er zij op gewezen dat als de specifieke lading van het deeltje verandert ( $\frac {q}{m}$ ) verandert ook de straal.

Dus de rotatieperiode T = . $\{\frac {2}{v}$ = $\frac {2.0 m}{q.0 B}$ . Het hangt niet af van de snelheid, dus de onderlinge positie van deeltjes met verschillende snelheden zal hetzelfde zijn.

De beweging van een geladen deeltje in een homogeen magnetisch veld.

In het meer gecompliceerde geval dat de hoek tussen de snelheid van het deeltje en de magnetische veldsterkte willekeurig is, zal het zich langs een spiraalvormige baan bewegen - geleidelijk ten koste van de evenwijdig aan het veld gerichte snelheidscomponent, en omtreksgewijs ten koste van de loodrecht daarop staande component.

Toepassingen van de lorentzkracht in de techniek

Kinescope

De kinescoop, die tot voor kort, toen hij werd vervangen door de LCD (flat screen), in elk televisietoestel zat, had niet kunnen werken zonder de Lorentz-kracht. Om een televisiebeeld op het scherm te vormen, wordt een smalle stroom elektronen door afbuigspoelen geleid die een lineair variërend magnetisch veld opwekken. De lijnspoelen bewegen de elektronenbundel van links naar rechts en terug, terwijl de kaderspoelen verantwoordelijk zijn voor de verticale beweging, waarbij de lopende bundel horizontaal van boven naar beneden wordt bewogen. Hetzelfde principe wordt gebruikt in oscilloscopen - instrumenten die worden gebruikt om elektrische wisselspanningen te bestuderen.

Massaspectrograaf

Een massaspectrograaf is een instrument dat gebruik maakt van de relatie tussen de rotatiestraal van een geladen deeltje en zijn specifieke lading. Het werkingsprincipe is als volgt:

Een bron van geladen deeltjes, die snelheid winnen door middel van een kunstmatig gecreëerd elektrisch veld, wordt in een vacuümkamer geplaatst om de invloed van luchtmoleculen uit te schakelen. De deeltjes vliegen uit de bron en komen via een cirkelboog op een fotografische plaat terecht, waar ze sporen op achterlaten. Afhankelijk van de specifieke lading, verandert de baanradius en dus het inslagpunt. Deze straal is gemakkelijk te meten en als men hem kent, kan de massa van het deeltje worden berekend. Met behulp van een massaspectrograaf is bijvoorbeeld de samenstelling van de maanbodem bestudeerd.

Lees ook: Wat zijn de beroepen in verband met elektriciteit

Cyclotron

De onafhankelijkheid van de periode en dus van de omwentelingsfrequentie van een geladen deeltje van zijn snelheid in aanwezigheid van een magnetisch veld wordt gebruikt in een apparaat, cyclotron genaamd, dat is ontworpen om deeltjes tot hoge snelheden te versnellen. De cyclotron bestaat uit twee holle metalen halve cilinders, duants (elk in de vorm van een Latijnse letter D), op korte afstand van elkaar geplaatst met de rechte zijden naar elkaar toe.

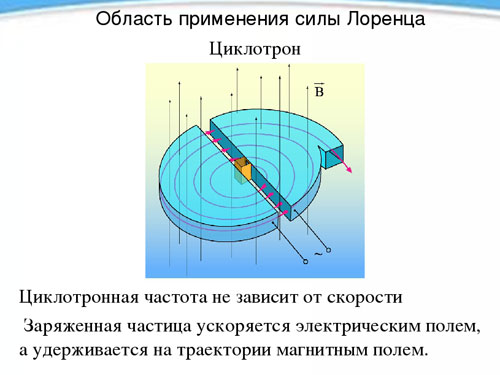
Cyclotron - toepassing van de Lorentzkracht.

De deeltjes worden in een constant homogeen magnetisch veld geplaatst en tussen de deeltjes wordt een wisselend elektrisch veld opgewekt, waarvan de frequentie gelijk is aan de rotatiefrequentie van het deeltje, die wordt bepaald door de magnetische veldsterkte en de specifieke lading. Omdat het deeltje tijdens de omwentelingsperiode tweemaal door het elektrische veld wordt beïnvloed (bij de overgang van de ene duant naar de andere), wordt het telkens versneld, waardoor de baanradius toeneemt, en op een bepaald moment, wanneer het de nodige snelheid heeft bereikt, vliegt het door het gat uit het apparaat. Op deze manier kan men een proton versnellen tot een energie van 20 MeVmega electronvolt).

Magnetron

Een apparaat genaamd een magnetron, die in elke microgolfovenis een ander voorbeeld van een apparaat dat werkt door gebruik te maken van de Lorentz-kracht. De magnetron creëert een sterk microgolfveld dat het interne volume van de oven waarin het voedsel wordt geplaatst, verwarmt. De magneten in de magnetron regelen het pad van de elektronen in de oven.

Het magnetisch veld van de aarde

In de natuur is de Lorentz-kracht zeer belangrijk voor de mensheid. Door zijn aanwezigheid kan het magnetisch veld van de aarde de mens beschermen tegen de dodelijke ioniserende straling van de ruimte. Het veld voorkomt dat geladen deeltjes het planeetoppervlak bombarderen en dwingt ze van richting te veranderen.

Verwante artikelen: