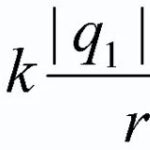Het begrip elektrische potentiaal is een belangrijke basis voor de theorie van de elektrostatica en de elektrodynamica. Inzicht in de essentie ervan is een eerste vereiste voor de verdere studie van deze takken van de natuurkunde.
Inhoud
Wat is een elektrische potentiaal
Laat een eenheidslading q geplaatst worden in het veld dat gecreëerd wordt door een stationaire lading Q, die beïnvloed wordt door Coulomb-kracht F=k*Qq/r.
Hierna wordt k=((1/4)*π* ε* ε), waarbij ε0 — is de elektrische constante (8,85*10-12 F/m), en ε diëlektrische constante van het medium.
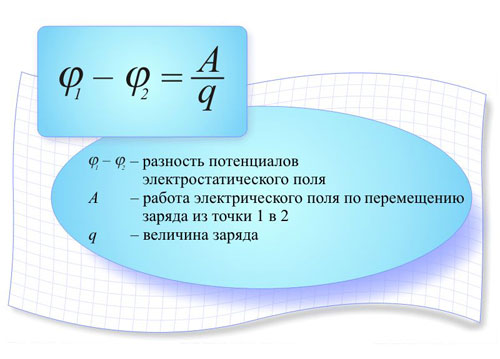
Ingebracht door lading kan bewegen onder invloed van deze kracht, en de kracht zal daarbij wat werk verrichten. Dit betekent dat een systeem van twee ladingen een potentiële energie heeft die afhangt van de grootte van beide ladingen en van de afstand tussen beide, en dat de grootte van deze potentiële energie onafhankelijk is van de grootte van de lading q. Hier wordt de definitie van de elektrische potentiaal geïntroduceerd - deze is gelijk aan de verhouding van de potentiële energie van het veld tot de grootte van de lading:
φ = W/q,
waarin W de potentiële energie is van het veld dat door het ladingenstelsel wordt gecreëerd, en de potentiaal de energiekarakteristiek van het veld. Om een lading q in een elektrisch veld over enige afstand te verplaatsen, is het nodig enige arbeid te verrichten om de Coulomb-kracht te overwinnen. De potentiaal van een punt is gelijk aan de arbeid die nodig is om een ladingseenheid van dat punt naar oneindig te verplaatsen. Er zij op gewezen dat:
- zal deze arbeid gelijk zijn aan het verlies van potentiële energie van de lading (A=W2-W1);
- is het werk onafhankelijk van de baan van de lading.
In het SI-stelsel is de eenheid van potentiaal één Volt (in de Russische literatuur aangeduid met V, in de buitenlandse literatuur met V). 1 V=1J/1Kl, d.w.z. dat we kunnen spreken over de potentiaal van een punt van 1 Volt, als het een arbeid van 1 Joule kost om een lading van 1Kl naar oneindig te verplaatsen. De naam is gekozen naar de Italiaanse natuurkundige Alessandro Volta, die een belangrijke bijdrage heeft geleverd aan de ontwikkeling van de elektrotechniek.
Om te visualiseren wat potentiaal is, kan het worden vergeleken met de temperatuur van twee lichamen of de temperatuur gemeten op verschillende punten in de ruimte. Temperatuur is een maat voor de verwarming van voorwerpen en potentiaal is een maat voor de elektrische lading. Men zegt dat het ene lichaam meer verhit wordt dan het andere; men kan ook zeggen dat het ene lichaam meer geladen is en het andere minder. Deze lichamen hebben verschillende potentiëlen.
De waarde van de potentiaal hangt af van de keuze van het coördinatenstelsel, zodat een bepaald niveau als nul moet worden genomen. Bij het meten van de temperatuur kan bijvoorbeeld de temperatuur van smeltend ijs als referentiegrens worden genomen. Voor een potentiaal wordt de potentiaal van een oneindig ver punt gewoonlijk als nul genomen, maar voor sommige toepassingen kan bijvoorbeeld de potentiaal van de aarde of de potentiaal van een van de windingen van een condensator als nul worden genomen.
Eigenschappen van een potentiaal
Enkele belangrijke eigenschappen van een potentiaal zijn
- indien het veld door verscheidene ladingen wordt opgewekt, zal de potentiaal op een bepaald punt gelijk zijn aan de algebraïsche (rekening houdend met het teken van de lading) som van de potentiëlen opgewekt door elk van de ladingen φ=φ1+φ2+φ3+φ4+φ5+...+φn;
- indien de afstanden tot de ladingen zodanig zijn dat de ladingen zelf als punt kunnen worden beschouwd, wordt de totale potentiaal berekend met de formule φ=k*(q1/r1+q2/r2+q3/r3+...+qn/rn), waarbij r de afstand is van de overeenkomstige lading tot het punt in kwestie.
Indien het veld gevormd wordt door een elektrische dipool (twee verwante ladingen van tegengesteld teken), is de potentiaal op elk punt op een afstand r van de dipool φ=k*p*cosά/r2waar:
- p is de elektrische arm van de dipool, gelijk aan q*l, waarbij l de afstand tussen de ladingen is;
- r is de afstand tot de dipool;
- ά is de hoek tussen de dipoolarm en de straalvector r.
Als het punt op de dipoolas ligt, cosά=1 en φ=k*p/r2.
Potentieel verschil
Indien twee punten een bepaald potentiaal hebben, en indien deze niet gelijk zijn, wordt gezegd dat er een potentiaalverschil bestaat tussen de twee punten. Er ontstaat een potentiaalverschil tussen punten
- waarvan de potentiaal wordt bepaald door ladingen van verschillende tekens;
- een punt met een potentiaal van elk teken van een lading en een punt met een nulpotentiaal
- punten met een potentiaal van gelijk teken maar verschillend in modulo.
Dat wil zeggen dat het potentiaalverschil niet afhangt van de keuze van het coördinatenstelsel. Een analogie kan worden getrokken met waterpoelen die zich op verschillende hoogten ten opzichte van het grondniveau (b.v. zeeniveau) bevinden.
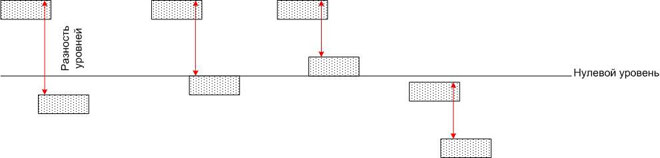
Het water van elk zwembad heeft een bepaalde potentiële energie, maar als men twee willekeurige zwembaden met elkaar verbindt door middel van een buis, zal er in elk zwembad een waterstroom zijn, waarvan de stroom niet alleen bepaald wordt door de grootte van de buis, maar ook door het verschil van potentiële energieën in het zwaartekrachtsveld van de aarde (dat wil zeggen, het verschil in hoogte). De absolute waarde van de potentiële energieën doet er in dit geval niet toe.
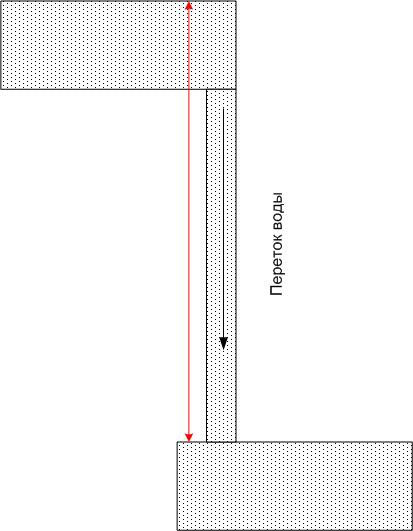
Evenzo, als je twee punten met verschillende potentiaal met een geleider verbindt, zal deze geleider een elektrische stroomniet alleen bepaald door de weerstand van de geleider, maar ook door het potentiaalverschil (maar niet door de absolute waarde ervan). De wateranalogie voortzettend, kunnen wij zeggen dat het water in het bovenste bekken spoedig zal opraken, en dat, tenzij een kracht kan worden gevonden om het water weer omhoog te brengen (zoals een pomp), de stroom zeer snel zal stoppen.
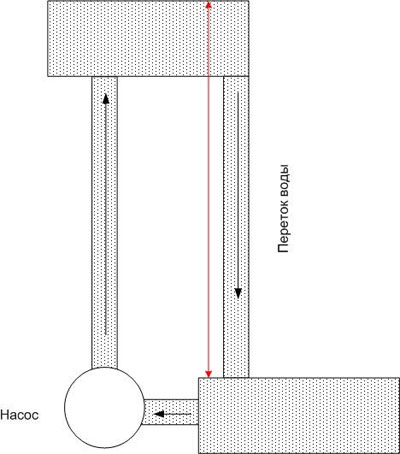
In een elektrische stroomkring is het net zo - om het potentiaalverschil op een bepaald niveau te houden, zal een kracht nodig zijn die ladingen (of liever, ladingsdragers) transporteert naar het punt met het hoogste potentiaal. Deze kracht wordt de elektromotorische kracht genoemd en wordt afgekort als EMF. EMV kunnen van verschillende aard zijn - elektrochemisch, elektromagnetisch, enz.
In de praktijk is vooral het potentiaalverschil tussen het beginpunt en het eindpunt van het traject van de ladingsdragers van belang. In dit geval wordt dit verschil een spanning genoemd, en in SI wordt het ook gemeten in volt. Men kan spreken van een spanning van 1 Volt als het veld de arbeid verricht van 1 Joule in het verplaatsen van een lading van 1 Coulomb van het ene punt naar het andere, d.w.z. 1V=1J/1Kl, en J/Kl kan ook de meeteenheid zijn van het potentiaalverschil.
Equipotentiaalvlakken
Indien de potentiaal van verschillende punten gelijk is en deze punten een oppervlak vormen, heet dit oppervlak equipotentiaal. Een bol omcirkeld rond een elektrische lading, bijvoorbeeld, heeft deze eigenschap, omdat het elektrisch veld in alle richtingen even sterk afneemt met de afstand.
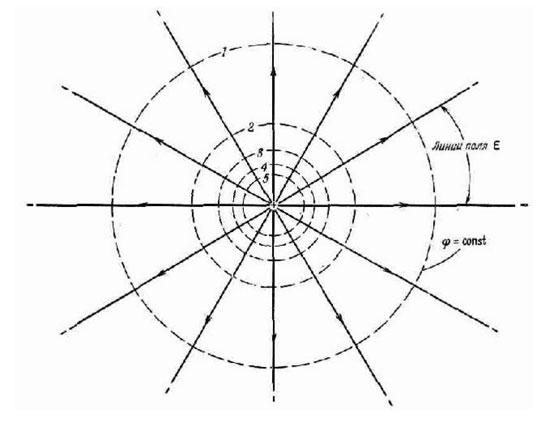
Alle punten op dit oppervlak hebben dezelfde potentiële energie, zodat er geen arbeid wordt verricht wanneer een lading op een dergelijke bol wordt verplaatst. De equipotentiaalvlakken van stelsels van meerdere ladingen hebben een complexere vorm, maar zij hebben één interessante eigenschap - zij snijden elkaar nooit. De krachtlijnen van het elektrisch veld staan altijd loodrecht op de oppervlakken met dezelfde potentiaal op elk van hun punten. Indien het equipotentiaalvlak wordt doorsneden door een vlak, verkrijgt men een lijn van gelijke potentialen. Het heeft dezelfde eigenschappen als een equipotentiaal oppervlak. In de praktijk hebben bijvoorbeeld punten op het oppervlak van een geleider die in een elektrostatisch veld zijn geplaatst, een gelijke potentiaal.
Als je eenmaal het concept van potentiaal en potentiaalverschil hebt begrepen, kun je beginnen meer te leren over elektrische verschijnselen. Maar niet eerder, want zonder een goed begrip van de basisbeginselen en -concepten is het niet mogelijk uw kennis te verdiepen.
Verwante artikelen: