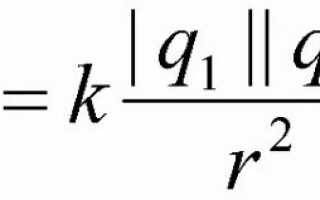Wet van Coulomb, definitie en formule - elektrische puntladingen en hun wisselwerking

Er is een interactiekracht tussen geladen lichamen, waardoor zij elkaar kunnen aantrekken of afstoten. De wet van Coulomb beschrijft deze kracht en toont de mate waarin zij werkt naar gelang van de grootte en de vorm van het lichaam zelf. Deze natuurkundige wet zal in dit artikel worden behandeld.

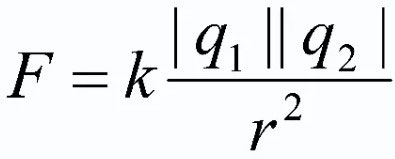
De formule van de wet van Coulomb.

Inhoud

1 Stationaire puntlasten
2 Charles Coulomb's torsie schalen
3 De evenredigheidscoëfficiënt k en de elektrische constante
4 Richting van de Coulomb-kracht en vectorformulering
5 Waar de wet van Coulomb in de praktijk van toepassing is
6 De richting van de kracht in de wet van Coulomb
7 Geschiedenis van de ontdekking

Stationaire puntlasten

De wet van Coulomb geldt voor stilstaande lichamen waarvan de afmetingen veel kleiner zijn dan hun afstand tot andere voorwerpen. Er is een elektrische puntlading op zulke lichamen. Bij het oplossen van fysische problemen worden de afmetingen van de betrokken lichamen verwaarloosd omdat zij niet veel belang hebben.

In de praktijk worden puntladingen in rust als volgt voorgesteld:

Een punt positief geladen lading q1.

In dit geval is q₁ en q₂ - zijn positief elektrische ladingen en zij worden beïnvloed door de Coulomb-kracht (niet weergegeven in de figuur). De grootte van puntobjecten doet er niet toe.

Let op! De rustende ladingen bevinden zich op een bepaalde afstand van elkaar, die in de problemen gewoonlijk wordt aangeduid met de letter r. Verderop in dit document zullen deze kosten in het luchtledige worden besproken.

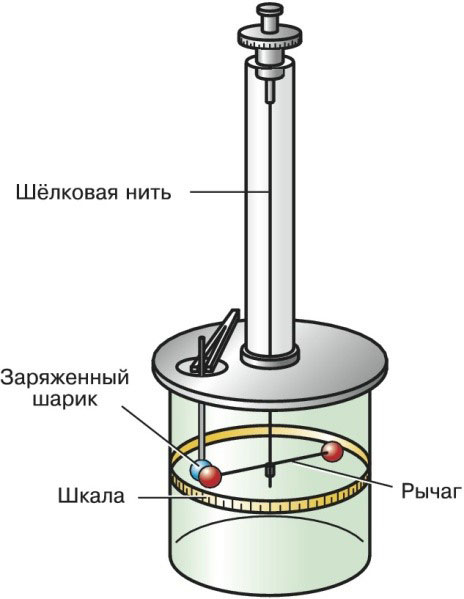
Charles Coulomb's torsie schalen

Dit apparaat, dat in 1777 door Coulomb werd ontwikkeld, hielp bij het afleiden van de afhankelijkheid van de kracht die later naar hem werd genoemd. Het wordt gebruikt om de interactie van puntladingen en magnetische polen te bestuderen.

Torsieschalen hebben een kleine zijden draad, geplaatst in een verticaal vlak, waaraan een uitgebalanceerde hefboom hangt. Er zijn puntladingen aan de uiteinden van de hefboom.

Onder invloed van externe krachten begint de hefboom horizontale bewegingen te maken. De hefboom zal in het vlak bewegen tot hij in evenwicht is door de elastische kracht van de draad.

Tijdens de beweging buigt de hefboom onder een bepaalde hoek van de verticale as af. Dit wordt genomen als d en wordt de draaihoek genoemd. Als men de waarde van deze parameter kent, kan men de torsie van de optredende krachten bepalen.

Lees ook: Wat is een elektrische stroom in eenvoudige termen

Charles Coulomb's torsie schalen zien er als volgt uit:

Charles Coulomb's torsie schalen.

De evenredigheidscoëfficiënt k en de elektrische constante 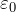$\varepsilon_0$

De formule van de wet van Coulomb heeft parameters k - de evenredigheidscoëfficiënt of $\varepsilon_0$ - elektrische constante. De elektrische constante $\varepsilon_0$ wordt in veel naslagwerken, leerboeken en op internet vermeld en hoeft niet te worden berekend! De evenredigheidscoëfficiënt in een vacuüm op basis van $\varepsilon_0$ kan worden gevonden volgens de bekende formule:

$k = \frac {1}{4}{pi}{varepsilon_0}$

Hier $\varepsilon_0=8.85\cdot 10^{ -12} \{C^2}{H^cdot m^2}$ - elektrische constante,

${3.14$ - het getal van pi,

$k=9{cdot 10^{9} \{\frac {H^cdot m^2}{C^2}$ - is de evenredigheidscoëfficiënt in vacuüm.

Meer informatie! Zonder de bovenstaande parameters te kennen is het niet mogelijk de interactiekracht tussen twee elektrische puntladingen te vinden.
Formulering en formule van de wet van Coulomb

Om het bovenstaande samen te vatten, moet een formele formulering van de hoofdwet van de elektrostatica worden gegeven. Dit neemt de vorm aan:

De interactiekracht van twee rustende puntladingen in een vacuüm is recht evenredig met het product van deze ladingen en omgekeerd evenredig met het kwadraat van de afstand tussen hen. En het product van ladingen moet modulo genomen worden!

$F=k} {q_1||cdot |q_2|}{r^2}$

In deze formule is q₁ en q₂- zijn puntladingen, de beschouwde lichamen; r² - de afstand op een vlak tussen deze lichamen, genomen als een kwadraat; k is de evenredigheidsfactor ( $9 keer 10^{9} \{\frac {H^cdot m^2}{C^2}$ voor een vacuüm).

De richting van de Coulomb-kracht en de vectorvorm van de formule

Om de formule volledig te begrijpen, kan de wet van Coulomb visueel worden voorgesteld:

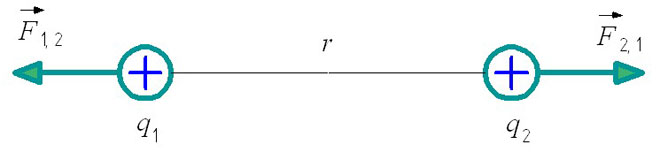
Coulomb-krachtrichting voor twee puntladingen met dezelfde polariteit.

F_1,2- is de interactiekracht van de eerste lading ten opzichte van de tweede.

F_2,1- is de interactiekracht van de tweede lading ten opzichte van de eerste.

Een belangrijke regel bij het oplossen van elektrostatische problemen is dat gelijke ladingen elkaar afstoten en gelijke ladingen elkaar aantrekken. Dit bepaalt de positie van de interactiekrachten in de figuur.

Als tegengestelde ladingen worden beschouwd, zullen de interactiekrachten naar elkaar toe gericht zijn, wat hun aantrekkingskracht vertegenwoordigt.

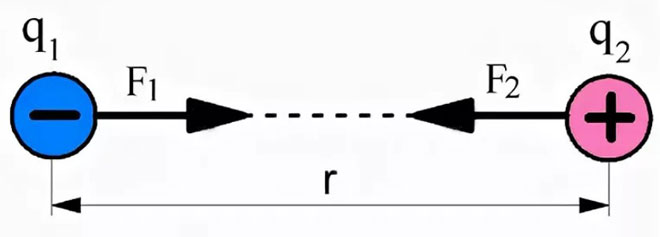
Coulomb-krachtrichting voor twee puntladingen met verschillende polariteit.

De formule van de basiswet van de elektrostatica kan in vectorvorm als volgt worden weergegeven

$\vec F_1_2= {1}{4 \pi}{r_1_2}{r_1_2^3}\cdot \vec r_1_2$

$\F_1_2$ - De kracht die werkt op de puntlading q1, op de ladingszijde q2,

${\an r_1_2}$ - is de straal-vector die lading q2 met lading q1 verbindt,

Lees ook: Hoe maak je thuis een elektronische printplaat?

$r=||vec r_1_2|$

Belangrijk! Door de formule in vectorvorm te schrijven, moeten de op elkaar inwerkende krachten van twee elektrische puntladingen op de as geprojecteerd worden om de tekens juist te plaatsen. Deze handeling is een formaliteit en wordt vaak mentaal verricht zonder aantekeningen.

Waar de wet van Coulomb in de praktijk van toepassing is

De basiswet van de elektrostatica is de belangrijkste ontdekking van Charles Coulomb, die op vele gebieden toepassing heeft gevonden.

Het werk van de beroemde natuurkundige werd gebruikt bij de uitvinding van verschillende apparaten, instrumenten en toestellen. Bijvoorbeeld, de bliksemafleider.

Bliksemafleiders worden gebruikt om huizen en gebouwen tijdens onweer tegen bliksem te beschermen. Dit verhoogt de mate van bescherming van elektrische apparatuur.

Bliksemafleiders werken volgens het volgende principe: sterke inductieladingen bouwen zich tijdens onweer geleidelijk op de grond op en worden vervolgens naar boven in de wolken meegevoerd. Dit genereert een groot elektrisch veld op de grond. Dicht bij de bliksemafleider wordt het elektrisch veld sterker, zodat een corona-elektrische lading wordt ontstoken vanuit de punt van het apparaat.

De op de grond gevormde lading wordt dan aangetrokken tot de lading op de wolk met het tegengestelde teken, zoals het volgens de wet van Coulomb zou moeten zijn. De lucht ondergaat dan een ionisatieproces en de elektrische veldsterkte wordt lager nabij het uiteinde van de bliksemafleider. Het risico dat de bliksem het gebouw treft, is dus minimaal.

Let op! Als een gebouw waarop een bliksemafleider is geïnstalleerd, wordt getroffen, zal er geen brand ontstaan en zal alle energie in de grond ontsnappen.

Op basis van de wet van Coulomb is een apparaat ontwikkeld dat "deeltjesversneller" wordt genoemd en waar tegenwoordig veel vraag naar is.

Dit apparaat creëert een sterk elektrisch veld, waardoor de energie van de deeltjes die het binnenkomen, toeneemt.

De richting van de krachten in de wet van Coulomb

Zoals hierboven vermeld, hangt de richting van de op elkaar inwerkende krachten van twee elektrische puntladingen af van hun polariteit. Dat wil zeggen, gelijke ladingen met dezelfde polariteit zullen elkaar afstoten en ladingen met tegengestelde polariteit zullen elkaar aantrekken.

Lees ook: Hoe maak je een metaaldetector met je eigen handen, beginnershulp

Coulombkrachten kunnen ook een radiusvector genoemd worden omdat worden ze geleid langs een lijn die tussen hen is getrokken.

In sommige natuurkundige problemen worden lichamen met een complexe vorm gegeven die niet kunnen worden opgevat als een elektrische puntlading, d.w.z. dat de afmetingen ervan worden verwaarloosd. In een dergelijke situatie moet het lichaam in kwestie worden opgesplitst in verschillende kleine delen en moet elk deel afzonderlijk worden berekend, met toepassing van de wet van Coulomb.

De krachtvectoren die verkregen worden door ze op te splitsen, worden opgeteld volgens de regels van de algebra en de meetkunde. Het resultaat is de resulterende kracht, die het antwoord is op het probleem. Deze oplossingsmethode wordt vaak de driehoekmethode genoemd.

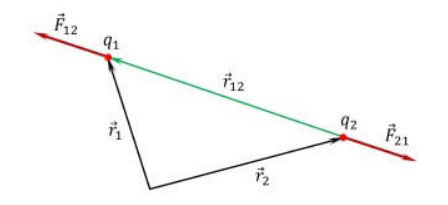
Richting van de Coulomb-krachtvectoren.

Geschiedenis van de ontdekking van de wet

De wisselwerking van twee puntladingen volgens de bovenstaande wet werd voor het eerst bewezen in 1785 door Charles Coulomb. De natuurkundige slaagde erin de waarheid van de geformuleerde wet te bewijzen met behulp van torsieschalen, waarvan het principe ook in het artikel werd gepresenteerd.

Coulomb bewees ook dat er geen elektrische lading is in een bolvormige condensator. Zo kwam hij tot de verklaring dat de grootte van de elektrostatische krachten kan worden veranderd door de afstand tussen de lichamen in kwestie te veranderen.

De wet van Coulomb is dus nog steeds de belangrijkste wet van de elektrostatica, op grond waarvan vele grote ontdekkingen zijn gedaan. In dit artikel is de officiële formulering van de wet gepresenteerd en zijn de samenstellende delen ervan in detail beschreven.

Verwante artikelen: