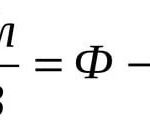電気容量は、静電気の基本概念の 1 つです。この用語は、電荷を蓄積する能力を指します。単一の導体の静電容量について話すことも、2 つ以上の導体のシステムの静電容量について話すこともできます。物理的なプロセスは似ています。

コンテンツ
静電容量に関する基本的な考え方
導体が電荷 q を受け取った場合、電位 φ が発生します。この電位は形状と環境に依存します。異なる導体と条件では、同じ電荷でも異なる電位が生じます。しかし、φ は常に q に比例します。
φ=Cq
係数 C は電気容量と呼ばれます。複数の導体 (通常は 2 つ) のシステムについて話している場合、1 つの導体 (クラッド) に電荷が与えられると、電位差または電圧 U が発生します。
U=Cq、したがって C=U/q
静電容量は、それを引き起こした電荷に対する電位差の比率として定義できます。 SI における容量の単位はファラッドです (以前はファラッドと呼ばれていました)。 1 F = 1 V/1 Cl。つまり、1 クーロンの電荷が 1 ボルトの電位差を生じさせるシステムの容量は 1 ファラッドです。 1 ファラッドは非常に大きな値です。実際には、ピコファラッド、ナノファラッド、マイクロファラッドなどの分数値が最も一般的に使用されます。
実際には、この接続により、単一セルよりも高い絶縁破壊電圧に耐えることができるバッテリーが可能になります。
コンデンサ容量の計算
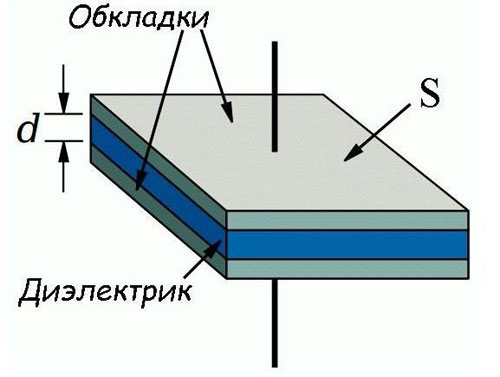
実際には、正規化された電気容量を持つ要素として、最も一般的に使用されるのは次のとおりです。 コンデンサ、誘電体によって分離された 2 つの平らな導体 (端子) で構成されます。このようなコンデンサの静電容量を計算する式は次のとおりです。
C=(S/d)*ε*ε0
どこ:
- C は静電容量、F です。
- S はインサートの面積、sq.m です。
- dはカバー間の距離、mです。
- ε0 - 電気定数、定数、8.854*10−12 F/m;
- ε - 誘電率、無次元値。
このことから、静電容量がカバーの面積に正比例し、導体間の距離に反比例することが容易に理解できます。静電容量は、カバーを分離する材料によっても影響を受けます。
静電容量を決定する量がコンデンサの電荷蓄積能力にどのように影響するかを理解するために、可能な限り高い静電容量を持つコンデンサを作成するための精神的な実験を行うことができます。
- 巻線の面積を増やすことができます。これにより、デバイスのサイズと重量が大幅に増加します。それらを分離する誘電体で層のサイズを縮小するために、それらは(チューブ、フラットブリケットなどに)丸められます。
- 別の方法は、カバー間の距離を縮めることです。誘電体層はカバー間の特定の電位差に耐えることができなければならないため、導体を互いに非常に近くに配置することは常に可能ではありません。厚さが薄いほど、絶縁ギャップの電気的強度は低くなります。このように使用すると、そのようなコンデンサの実用的なアプリケーションが無意味になる瞬間が来るでしょう - それは非常に低い電圧でしか動作しません.
- 誘電体の電気透過率を高めます。この方法は、現在の生産技術の発展にかかっています。絶縁材料は、透磁率が高いだけでなく、優れた誘電特性も備えていなければならず、必要な周波数範囲でそのパラメータを保持する必要があります (コンデンサが動作する周波数が高くなると、誘電特性は低下します)。
球形または円筒形のコンデンサは、一部の特殊または研究設備で使用できます。
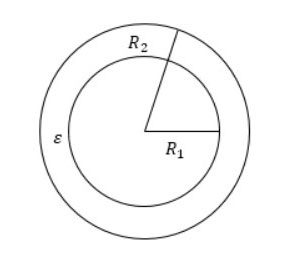
球状コンデンサの容量は、次の式で計算できます。
C=4*π*ε0 *R1R2/(R2-R1)
ここで、R は球の半径で、π=3.14 です。
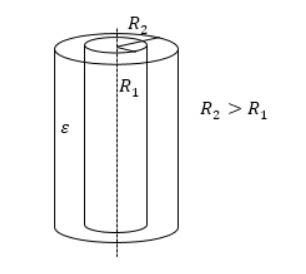
円筒形コンデンサの設計では、静電容量は次のように計算されます。
C=2*π*ε*ε0 *l/ln(R2/R1)
l は円柱の高さ、R1 と R2 は円柱の半径です。
原則として、どちらの式もフラット コンデンサの式と変わりません。静電容量は常に、端子の長さ寸法、端子間の距離、および誘電体の特性によって決まります。
コンデンサを直列および並列に接続する
コンデンサ接続可能 直列または並列、新しい特性を持つセットを作成します。
並列接続
コンデンサが並列に接続されている場合、結果として得られるバッテリーの総静電容量は、そのコンポーネントのすべての静電容量の合計に等しくなります。バッテリーが同じ設計のコンデンサーで構成されている場合、すべてのプレートの面積を合計すると考えることができます。この場合、バッテリーの各要素の電圧は同じになり、電荷が加算されます。並列に接続された 3 つのコンデンサの場合:
- U=U1=U2=U3;
- q=q1+q2+q3;
- C=C1+C2+C3.
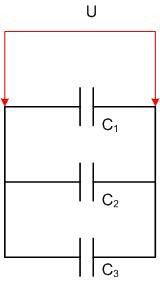
直列接続
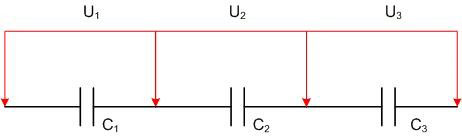
直列に接続すると、各静電容量の電荷は同じになります。
q1=q2=q3=q
総電圧は次のように分配されます。 コンデンサの静電容量に:
- う1=q/C1;
- う2=q/C2;
- う3=q/C3.
すべてのコンデンサが同じ場合、同じ電圧がそれぞれにかかります。総静電容量は次のように求められます。
C=q/( U1+U2+U3)、したがって 1/C=( U1+U2+U3)/q=1/C1+1/С2+1/С3.
工学におけるコンデンサの応用
コンデンサを電気エネルギーの蓄電池として使用することは理にかなっています。そのため、蓄えられたエネルギーが小さく、誘電体を介した電荷の漏れによる急速な自己放電のために、電気化学的電源 (ガルバニ電池、コンデンサ) と競合することはできません。しかし、エネルギーを長期間蓄え、ほぼ瞬時に放出する能力は広く利用されています。この特性は、写真用のフラッシュ ランプやレーザー励起用のランプに使用されます。
コンデンサは、無線工学および電子工学で非常に一般的です。コンデンサは、回路の周波数保持要素の 1 つとして共振回路で使用されます (もう 1 つの要素はインダクタンスです)。交流成分を閉じ込めずに直流を遮断するコンデンサの能力も利用されます。このようなアプリケーションは、増幅段を分割して、一方の段の DC モードが他方の段に及ぼす影響を排除するのに一般的です。大容量コンデンサは、電源の平滑フィルタとして使用されます。また、その特性が有用であることが証明されているその他の無数のコンデンサ アプリケーションもあります。
いくつかの実用的なコンデンサ設計
実際には、さまざまなフラット コンデンサの設計が使用されています。デバイスの設計によって、その特性と用途が決まります。
可変コンデンサ
一般的なタイプの可変コンデンサ (AC コンデンサ) は、空気または固体絶縁体によって分離された可動プレートと固定プレートのブロックで構成されます。可動プレートは軸を中心に回転し、重なり合う領域を増減します。可動ユニットが引き出されると、電極間ギャップは変化しませんが、プレート間の平均距離も増加します。絶縁体の誘電率も変化しません。静電容量は、カバーの面積とそれらの間の平均距離を変更することによって調整されます。

酸化物コンデンサ
このタイプのコンデンサは、以前は電解コンデンサと呼ばれていました。これは、電解質に浸した紙の誘電体によって分離された 2 つの箔のストリップで構成されています。最初のストリップは 1 つのカバーとして機能し、2 番目のストリップは電解質として機能します。誘電体は、金属ストリップの 1 つにある酸化物の薄い層であり、2 番目のストリップは集電体として機能します。
酸化物層が非常に薄く、電解質がそれに近いため、適度なサイズで非常に大きな容量を得ることができました。これの代償は動作電圧が低いことです - 酸化物層は高い電気的強度を持っていません.動作電圧が高くなると、コンデンサのサイズを大幅に大きくする必要があります。
もう1つの問題は、酸化物が一方向の導電性を持っていることです。そのため、このようなコンデンサは、極性を遵守するDC回路でのみ使用されます。
イオニスタ
上に示したように、伝統的な増加方法は、 コンデンサ 自然な制限があります。したがって、本当の突破口はイオニスタの作成でした。
このデバイスは、コンデンサとバッテリの中間と見なされますが、本質的にはコンデンサです。
二重電気層の使用により、コイル間の距離が大幅に短縮されます。反対の電荷を持つイオンの層が層として機能します。発泡多孔質材料により、カバーの表面積を大幅に増やすことができます。その結果、数百ファラッドまでの容量を持つスーパーキャパシタを得ることが可能です。このようなデバイスに固有の病気は、動作電圧が低いことです (通常は 10 ボルト以内)。
技術の発展は止まらず、多くの分野のランプがバイポーラトランジスタに置き換えられ、さらにユニポーラ三極管に置き換えられました。インダクタは、可能な限り回路設計で取り除かれています。そして、コンデンサは2世紀に渡ってその地位を放棄せず、ライデン瓶の発明以来、その設計は根本的に変わっておらず、そのキャリアの終わりの見通しは観察されていません.
関連記事: