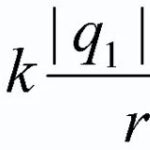લોરેન્ટ્ઝ ફોર્સ અને ડાબા હાથનો નિયમ. ચુંબકીય ક્ષેત્રમાં ચાર્જ થયેલા કણોની ગતિ

ચુંબકીય ક્ષેત્રમાં મૂકવામાં આવે છે વાહક...જેના દ્વારા વિદ્યુત પ્રવાહ... ઇલેક્ટ્રિક પ્રવાહએમ્પીયર બળથી પ્રભાવિત છે $F_A$ , અને તેની તીવ્રતાની ગણતરી નીચેના સૂત્ર દ્વારા કરી શકાય છે:

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

જ્યાં $આઈ$ અને $l$ - વર્તમાન તાકાત અને કંડક્ટરની લંબાઈ, $બી$ - ચુંબકીય ક્ષેત્રનું ઇન્ડક્શન, $\આલ્ફા$ - વર્તમાન અને ચુંબકીય ઇન્ડક્શનની દિશાઓ વચ્ચેનો ખૂણો. તો આવું કેમ થઈ રહ્યું છે?

લોરેન્ટ્ઝ ફોર્સ. ચુંબકીય ક્ષેત્રમાં ચાર્જ થયેલ કણની ગતિ.

સામગ્રી

1 લોરેન્ટ્ઝ બળ શું છે - વ્યાખ્યા, જ્યારે તે થાય છે, સૂત્ર મેળવવું
2 ડાબા હાથના નિયમનો ઉપયોગ કરીને લોરેન્ટ્ઝ બળની દિશા નક્કી કરવી
3 ચુંબકીય ક્ષેત્રમાં ચાર્જ થયેલ કણની હિલચાલ
4 એન્જિનિયરિંગમાં લોરેન્ટ્ઝ ફોર્સનો ઉપયોગ

લોરેન્ટ્ઝ બળ શું છે - વ્યાખ્યા, જ્યારે તે ઉદ્ભવે છે, સૂત્ર મેળવવું

તે જાણીતું છે કે ઇલેક્ટ્રિક પ્રવાહ એ ચાર્જ કરેલા કણોની ક્રમબદ્ધ હિલચાલ છે. તે પણ સ્થાપિત કરવામાં આવ્યું છે કે ચુંબકીય ક્ષેત્રમાં ગતિ કરતી વખતે, આ દરેક કણો બળને આધિન છે. બળ ઉત્પન્ન થવા માટે, કણ ગતિમાં હોવો જોઈએ.

લોરેન્ટ્ઝ બળ એ બળ છે જે ચુંબકીય ક્ષેત્રમાં ફરતા વિદ્યુત ચાર્જ કણ પર કાર્ય કરે છે. તેની દિશા એ પ્લેન માટે ઓર્થોગોનલ છે જેમાં કણના વેગ વેક્ટર અને ચુંબકીય ક્ષેત્રની તાકાત રહે છે.લોરેન્ટ્ઝ ફોર્સ એમ્પીયર ફોર્સ છે. તે જાણીને, અમે લોરેન્ટ્ઝ બળ માટે એક સૂત્ર મેળવી શકીએ છીએ.

વાહકના પટને પસાર કરવા માટે કણ માટે જરૂરી સમય, $t = \frac {l}{v}$ જ્યાં $l$ - સેગમેન્ટની લંબાઈ છે, $વિ$ - કણનો વેગ. કંડક્ટરના ક્રોસ સેક્શન દ્વારા આ સમય દરમિયાન વહન કરાયેલ કુલ ચાર્જ, $Q = I\cdot t$ . અગાઉની સમાનતામાંથી સમયનું મૂલ્ય અહીં બદલીને, આપણી પાસે છે

$Q = \frac {I\cdot l}{v}$ (2)

તે જ સમયે $F_A=F_L\cdot N$ જ્યાં $એન$ - ગણવામાં આવેલ વાહકમાં કણોની સંખ્યા છે. તે જ સમયે $N = \frac {Q}{q}$ જ્યાં $q$ - એક કણનો ચાર્જ છે. નું મૂલ્ય સૂત્રમાં બદલીને $પ્ર$ (2) થી, કોઈ મેળવી શકે છે:

$N = \frac {I\cdot l}{v\cdot q}$

આમ,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

(1) નો ઉપયોગ કરીને, અગાઉના અભિવ્યક્તિ તરીકે લખી શકાય છે

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

કાપ અને સ્થાનાંતરણ પછી લોરેન્ટ્ઝ બળની ગણતરી માટેનું સૂત્ર દેખાય છે

$F_L = q\cdot v\cdot B\cdot sin\alpha$

આપેલ છે કે સૂત્ર બળના મોડ્યુલસ માટે લખાયેલ છે, તે નીચે પ્રમાણે લખવું જોઈએ:

આ પણ વાંચો: એમ્પીયર ને વોટ અને બેક માં કેવી રીતે રૂપાંતરિત કરવું?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

ત્યારથી $sin\alpha = sin(180^{\circ} -\alpha)$ , લોરેન્ટ્ઝ મોડ્યુલસની ગણતરી માટે તે કોઈ વાંધો નથી કે વેગ વર્તમાન બળની દિશામાં નિર્દેશિત છે કે તેની વિરુદ્ધ, અને આપણે કહી શકીએ કે $\આલ્ફા$ - એ કણના વેગ વેક્ટર અને ચુંબકીય ઇન્ડક્શન દ્વારા રચાયેલ કોણ છે.

સૂત્રને વેક્ટર સ્વરૂપમાં લખવાથી નીચે મુજબ દેખાશે:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}$

$[\vec{v}\વાર \vec{B}$ - વેક્ટર ઉત્પાદન છે, જેનું પરિણામ એ એક મોડ્યુલસ સાથે વેક્ટર છે $v\cdot B\cdot sin\alpha$ .

સૂત્ર (3) ના આધારે, આપણે તારણ કાઢી શકીએ છીએ કે ઇલેક્ટ્રિક પ્રવાહ અને ચુંબકીય ક્ષેત્રની દિશાઓની લંબરૂપતાના કિસ્સામાં લોરેન્ટ્ઝ બળ મહત્તમ છે, એટલે કે $આલ્ફા = 90^{\circ}$ અને જ્યારે તેઓ સમાંતર હોય ત્યારે અદૃશ્ય થઈ જાય છે ( $\alpha = 0^{\circ}$ ).

યાદ રાખો કે સાચો જથ્થાત્મક જવાબ આપવા માટે - ઉદાહરણ તરીકે, સમસ્યાઓ હલ કરતી વખતે - વ્યક્તિએ SI એકમોનો ઉપયોગ કરવો જોઈએ, જેમાં ચુંબકીય ઇન્ડક્શન ટેસ્લાસમાં માપવામાં આવે છે (1 ટેસ્લા = 1 kg-c⁻²-એ⁻¹), ન્યુટનમાં બળ (1 N = 1 kg-m/s²), એમ્પીયરમાં વર્તમાન, કુલોનમાં ચાર્જ (1 Cl = 1 A-s), મીટરમાં લંબાઈ, m/s માં ઝડપ.

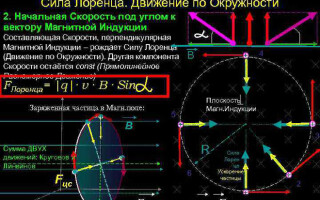
ડાબા હાથના નિયમનો ઉપયોગ કરીને લોરેન્ટ્ઝ બળની દિશા નક્કી કરવી

મેક્રો ઑબ્જેક્ટ્સની દુનિયામાં લોરેન્ટ્ઝ ફોર્સ એમ્પીયર ફોર્સ તરીકે દેખાય છે, તેથી અમે તેની દિશા નક્કી કરવા માટે ડાબા હાથના નિયમનો ઉપયોગ કરી શકીએ છીએ.

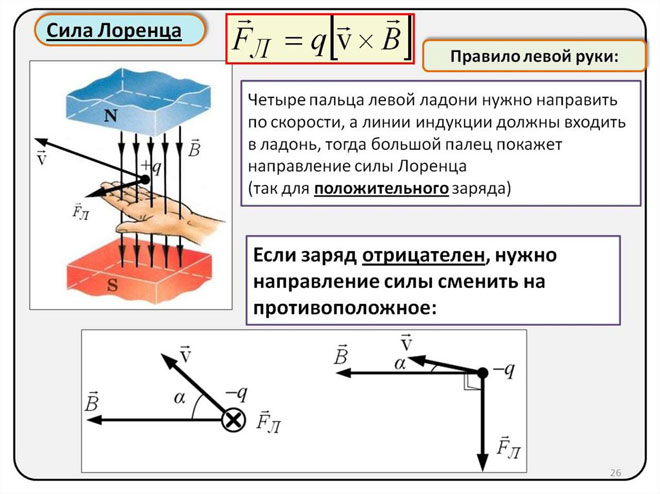
ડાબા હાથના નિયમનો ઉપયોગ કરીને લોરેન્ટ્ઝ બળની દિશા નક્કી કરવી.

જો તમે તમારા ડાબા હાથને એવી રીતે મૂકો છો કે તમારી ખુલ્લી હથેળી ચુંબકીય ક્ષેત્રની રેખાઓની સામે અને તેની સામે લંબરૂપ હોય, તો ચાર આંગળીઓને પ્રવાહની દિશામાં લંબાવવી જોઈએ, તો લોરેન્ટ્ઝ બળ તમારા અંગૂઠાને જ્યાં વાળવું જોઈએ તે તરફ નિર્દેશિત કરવામાં આવશે. , નિર્દેશ કરે છે.

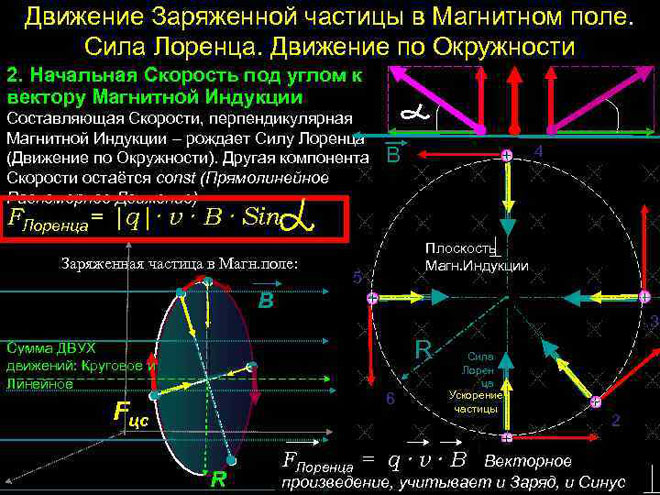
ચુંબકીય ક્ષેત્રમાં ચાર્જ થયેલ કણની હિલચાલ

સૌથી સરળ કિસ્સામાં, એટલે કે ચુંબકીય ઇન્ડક્શનના વેક્ટરની ઓર્થોગોનાલિટી અને કણના વેગ સાથે, લોરેન્ટ્ઝ બળ, વેગ વેક્ટરને લંબરૂપ હોવાથી, માત્ર તેની દિશા બદલી શકે છે. વેગની તીવ્રતા, તેથી, અને ઊર્જા યથાવત રહેશે. તેથી લોરેન્ટ્ઝ બળ મિકેનિક્સમાં કેન્દ્રબિંદુ બળ સાથે સામ્યતા દ્વારા કાર્ય કરે છે, અને કણ વર્તુળમાં ફરે છે.

આ પણ વાંચો: એક કિલોવોટમાં કેટલા વોટ છે?

ન્યુટનના II ના કાયદા અનુસાર ( $F = m\cdot a$ ) આપણે કણના પરિભ્રમણની ત્રિજ્યા નક્કી કરી શકીએ છીએ:

$N = \frac {m\cdot v}{q\cdot B}$ .

એ નોંધવું જોઈએ કે જેમ જેમ કણોનો ચોક્કસ ચાર્જ બદલાય છે ( $\frac {q}{m}$ ), ત્રિજ્યા પણ બદલાય છે.

આ કિસ્સામાં, પરિભ્રમણનો સમયગાળો T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . તે વેગ પર આધારિત નથી, તેથી વિવિધ વેગવાળા કણોની પરસ્પર સ્થિતિ સમાન હશે.

સજાતીય ચુંબકીય ક્ષેત્રમાં ચાર્જ થયેલ કણની ગતિ.

વધુ જટિલ કિસ્સામાં, જ્યારે કણના વેગ અને ચુંબકીય ક્ષેત્રની મજબૂતાઈ વચ્ચેનો ખૂણો મનસ્વી હોય છે, ત્યારે તે એક હેલિકલ ટ્રેજેક્ટરી સાથે આગળ વધે છે - ક્રમશઃ ક્ષેત્રની સમાંતર નિર્દેશિત વેગ ઘટકના ભોગે, અને તેના પ્રભાવ હેઠળ પરિઘ સાથે. લંબ ઘટક.

એન્જિનિયરિંગમાં લોરેન્ટ્ઝ ફોર્સનો ઉપયોગ

કાઈનસ્કોપ

કાઇનસ્કોપ, જે તાજેતરમાં સુધી, જ્યારે તેને એલસીડી (ફ્લેટ સ્ક્રીન) દ્વારા બદલવામાં આવ્યું હતું, ત્યારે તે દરેક ટીવી સેટમાં હતું, તે લોરેન્ટ્ઝ ફોર્સ વિના કામ કરી શકતું ન હતું. ઇલેક્ટ્રોનના સાંકડા પ્રવાહમાંથી સ્ક્રીન પર ટેલિવિઝન ઇમેજ બનાવવા માટે, રેખીય રીતે બદલાતા ચુંબકીય ક્ષેત્ર બનાવવા માટે ડિફ્લેક્શન કોઇલનો ઉપયોગ કરવામાં આવે છે.લાઇન કોઇલ ઇલેક્ટ્રોન બીમને ડાબેથી જમણે અને પાછળ ખસેડે છે, ફ્રેમ કોઇલ ઊભી હિલચાલ માટે જવાબદાર છે, બીમને ઉપરથી નીચે સુધી આડી રીતે ખસેડે છે. માં સમાન સિદ્ધાંતનો ઉપયોગ થાય છે ઓસિલોસ્કોપ - વૈકલ્પિક વિદ્યુત વોલ્ટેજનો અભ્યાસ કરવા માટે.

માસ સ્પેક્ટ્રોગ્રાફ

માસ સ્પેક્ટ્રોગ્રાફ એ એક ઉપકરણ છે જે તેના ચોક્કસ ચાર્જ પર ચાર્જ થયેલ કણના પરિભ્રમણ ત્રિજ્યાની અવલંબનનો ઉપયોગ કરે છે. તેના ઓપરેશનનો સિદ્ધાંત નીચે મુજબ છે:

હવાના અણુઓના પ્રભાવને દૂર કરવા માટે કૃત્રિમ રીતે બનાવેલા ઇલેક્ટ્રિક ફિલ્ડના માધ્યમથી ઝડપ મેળવતા ચાર્જ થયેલા કણોનો સ્ત્રોત વેક્યૂમ ચેમ્બરમાં મૂકવામાં આવે છે. કણો સ્ત્રોતમાંથી ઉડી જાય છે અને, વર્તુળના ચાપમાંથી પસાર થતાં, ફોટોગ્રાફિક પ્લેટને અથડાવે છે, તેના પર નિશાન છોડી દે છે. ચોક્કસ ચાર્જ પર આધાર રાખીને, બોલ ત્રિજ્યા અને તેથી, અસર બિંદુ બદલાય છે. આ ત્રિજ્યા માપવામાં સરળ છે, અને તેને જાણીને, તમે કણના દળની ગણતરી કરી શકો છો. સામૂહિક સ્પેક્ટ્રોગ્રાફનો ઉપયોગ કરીને, ઉદાહરણ તરીકે, ચંદ્રની જમીનની રચનાનો અભ્યાસ કરવામાં આવ્યો હતો.

આ પણ વાંચો: વીજળી સાથે સંબંધિત કેટલાક વ્યવસાયો શું છે

સાયક્લોટ્રોન

સમયગાળાની સ્વતંત્રતા, અને તેથી ચુંબકીય ક્ષેત્રની હાજરીમાં તેની ગતિથી ચાર્જ થયેલ કણની પરિભ્રમણ આવર્તનનો ઉપયોગ સાયક્લોટ્રોન નામના ઉપકરણમાં થાય છે, જે કણોને ઉચ્ચ ઝડપે વેગ આપવા માટે રચાયેલ છે. સાયક્લોટ્રોન એ બે હોલો મેટલ અર્ધ-સિલિન્ડર છે, ડ્યુઅન્ટ્સ (દરેકનો આકાર લેટિન અક્ષર D જેવો છે), તેમની સીધી બાજુઓ એકબીજાની સામે ટૂંકા અંતરે મૂકવામાં આવે છે.

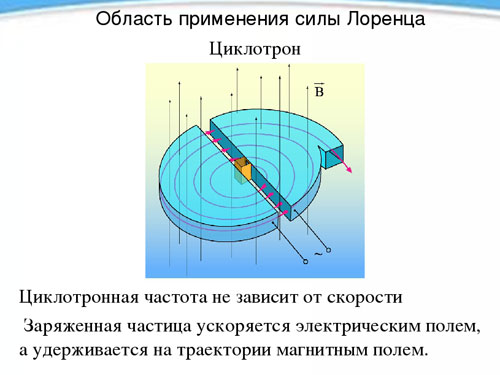
સાયક્લોટ્રોન - લોરેન્ટ્ઝ બળનો ઉપયોગ.

ડ્યુઅન્ટ્સ સતત સજાતીય ચુંબકીય ક્ષેત્રમાં મૂકવામાં આવે છે, અને તેમની વચ્ચે વૈકલ્પિક ઇલેક્ટ્રિક ક્ષેત્ર બનાવવામાં આવે છે, જેની આવર્તન કણોના પરિભ્રમણની આવર્તન જેટલી હોય છે, જે ચુંબકીય ક્ષેત્રની શક્તિ અને ચોક્કસ ચાર્જ દ્વારા નિર્ધારિત થાય છે.પરિભ્રમણ સમયગાળા દરમિયાન (એક ડ્યુઅન્ટથી બીજામાં સંક્રમણ દરમિયાન) બે વાર ઇલેક્ટ્રિક ફિલ્ડના સંપર્કમાં આવવાથી, કણ દરેક વખતે ઝડપી બને છે, ટ્રેજેક્ટરી ત્રિજ્યામાં વધારો કરે છે, અને ચોક્કસ ક્ષણે, જરૂરી વેગ પ્રાપ્ત કર્યા પછી, તે બહાર ઉડી જાય છે. છિદ્ર દ્વારા ઉપકરણ. આ રીતે કોઈ પ્રોટોનને 20 MeV ની ઉર્જા સુધી વેગ આપી શકે છેમેગા ઇલેક્ટ્રોનવોલ્ટ).

મેગ્નેટ્રોન

મેગ્નેટ્રોન નામનું ઉપકરણ, જે દરેકમાં સ્થાપિત થયેલ છે માઇક્રોવેવ પકાવવાની નાની ભઠ્ઠીLorentz ફોર્સનો ઉપયોગ કરતા ઉપકરણોનો બીજો પ્રતિનિધિ છે. મેગ્નેટ્રોનનો ઉપયોગ શક્તિશાળી માઇક્રોવેવ ક્ષેત્ર બનાવવા માટે થાય છે જે પકાવવાની નાની ભઠ્ઠીના આંતરિક વોલ્યુમને ગરમ કરે છે જ્યાં ખોરાક મૂકવામાં આવે છે. તેમાં સમાવિષ્ટ ચુંબક ઉપકરણની અંદરના ઇલેક્ટ્રોનના માર્ગને ઠીક કરે છે.

પૃથ્વીનું ચુંબકીય ક્ષેત્ર

અને પ્રકૃતિમાં, લોરેન્ટ્ઝ બળ માનવજાત માટે અત્યંત મહત્વપૂર્ણ ભૂમિકા ભજવે છે. તેની હાજરી પૃથ્વીના ચુંબકીય ક્ષેત્રને અવકાશના ઘાતક આયનાઇઝિંગ કિરણોત્સર્ગથી મનુષ્યને બચાવવા માટે પરવાનગી આપે છે. આ ક્ષેત્ર ચાર્જ્ડ કણોને ગ્રહની સપાટી પર બોમ્બમારો કરતા અટકાવે છે, તેમને દિશા બદલવાની ફરજ પાડે છે.

સંબંધિત લેખો: