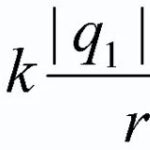બે બિંદુઓ વચ્ચે સંભવિત અને સંભવિત તફાવત શું છે

ઈલેક્ટ્રિક પોટેન્શિયલનો ખ્યાલ એ ઈલેક્ટ્રોસ્ટેટિક્સ અને ઈલેક્ટ્રોડાયનેમિક્સના સિદ્ધાંતના મહત્વના પાયામાંનો એક છે. ભૌતિકશાસ્ત્રના આ વિભાગોના વધુ અભ્યાસ માટે તેના સારને સમજવું એ પૂર્વશરત છે.

ઇલેક્ટ્રિક સંભવિત શું છે

એકમ ચાર્જ q ને સ્થિર ચાર્જ Q દ્વારા બનાવેલ ક્ષેત્રમાં મૂકવા દો, જેના પર કુલોમ્બ બળ F=k*Qq/r.

આ પછી k=((1/4)*π* ε* ε), જ્યાં ε_{0 —} વિદ્યુત સ્થિરાંક છે (8.85*10^-12 F/m), અને ε માધ્યમનો ડાઇલેક્ટ્રિક સ્થિરાંક.

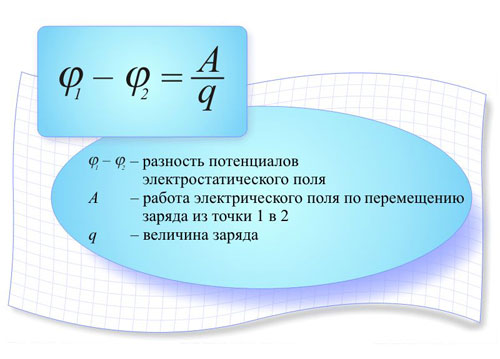
દ્વારા રજૂઆત કરવામાં આવી હતી ચાર્જ આ બળની ક્રિયા હેઠળ આગળ વધી શકે છે, અને બળ થોડું કામ કરશે. આનો અર્થ એ છે કે બે ચાર્જની સિસ્ટમમાં સંભવિત ઊર્જા હોય છે જે બંને ચાર્જની તીવ્રતા અને તેમની વચ્ચેના અંતર પર આધાર રાખે છે, અને આ સંભવિત ઊર્જાનું મૂલ્ય ચાર્જ q ની તીવ્રતા પર આધારિત નથી. આ તે છે જ્યાં ઇલેક્ટ્રિક સંભવિતની વ્યાખ્યા રજૂ કરવામાં આવી છે: તે ક્ષેત્રની સંભવિત ઊર્જાના ચાર્જની તીવ્રતાના ગુણોત્તર સમાન છે:

φ=W/q,

જ્યાં ડબલ્યુ એ ચાર્જિસ સિસ્ટમ દ્વારા બનાવવામાં આવેલ ક્ષેત્રની સંભવિત ઊર્જા છે, અને સંભવિત એ ક્ષેત્રની ઊર્જા લાક્ષણિકતા છે. ઇલેક્ટ્રિક ફિલ્ડમાં ચાર્જ q ને અમુક અંતર સુધી ખસેડવા માટે, કુલોમ્બ બળને દૂર કરવા માટે થોડું કામ કરવું જરૂરી છે.બિંદુની સંભવિતતા એ એકમ ચાર્જને તે બિંદુથી અનંત સુધી ખસેડવા માટે જે કાર્ય લે છે તેના બરાબર છે. એ નોંધવું જોઈએ કે:

• આ કાર્ય ચાર્જની સંભવિત ઉર્જા (A=W₂-ડબલ્યુ₁);
• કાર્ય ચાર્જના માર્ગ પર આધારિત નથી.

SI સિસ્ટમમાં, સંભવિતનું એકમ એક વોલ્ટ છે (રશિયન ભાષાના સાહિત્યમાં V દ્વારા સૂચવવામાં આવે છે, વિદેશી સાહિત્યમાં V). 1 V=1J/1 Kl, એટલે કે, આપણે 1 વોલ્ટના બિંદુની સંભવિતતા વિશે વાત કરી શકીએ છીએ, જો તેને 1 Kl ના ચાર્જને અનંતમાં ખસેડવા માટે 1 જૌલનું કામ લાગે છે. આ નામ ઇટાલિયન ભૌતિકશાસ્ત્રી એલેસાન્ડ્રો વોલ્ટાના માનમાં પસંદ કરવામાં આવ્યું હતું, જેમણે ઇલેક્ટ્રિકલ એન્જિનિયરિંગના વિકાસમાં મહત્વપૂર્ણ યોગદાન આપ્યું હતું.

સંભવિત શું છે તેની કલ્પના કરવા માટે, તેની તુલના બે શરીરના તાપમાન અથવા અવકાશમાં વિવિધ બિંદુઓ પર માપવામાં આવતા તાપમાન સાથે કરી શકાય છે. તાપમાન એ વસ્તુઓને ગરમ કરવાનું માપ છે, અને સંભવિત એ ઇલેક્ટ્રિક ચાર્જનું માપ છે. એક શરીર બીજા કરતાં વધુ ગરમ હોવાનું કહેવાય છે, અને એવું પણ કહી શકાય કે એક શરીર વધુ ચાર્જ કરે છે અને બીજું ઓછું ચાર્જ કરે છે. આ સંસ્થાઓમાં વિવિધ ક્ષમતાઓ હોય છે.

સંભવિતનું મૂલ્ય સંકલન પ્રણાલીની પસંદગી પર આધારિત છે, તેથી કેટલાક સ્તરને શૂન્ય તરીકે લેવા જરૂરી છે. તાપમાન માપતી વખતે, ઉદાહરણ તરીકે, પીગળતા બરફનું તાપમાન સંદર્ભ સીમા તરીકે લઈ શકાય છે. સંભવિત માટે, અનંત દૂરના બિંદુની સંભવિતતાને સામાન્ય રીતે શૂન્ય તરીકે લેવામાં આવે છે, પરંતુ કેટલીક સમસ્યાઓ માટે, પૃથ્વીની સંભવિતતા અથવા કેપેસિટરના કવરમાંથી એકની સંભવિતતા, ઉદાહરણ તરીકે, શૂન્ય તરીકે લઈ શકાય છે.

સંભવિત ગુણધર્મો

સંભવિતના મહત્વના ગુણધર્મોમાં નીચેનાનો સમાવેશ થાય છે:

• જો ક્ષેત્ર ઘણા ચાર્જ દ્વારા બનાવવામાં આવે છે, તો ચોક્કસ બિંદુ પર સંભવિત દરેક ચાર્જ દ્વારા બનાવવામાં આવેલ સંભવિતતાના સરવાળા બીજગણિત (ચાર્જના સંકેતને ધ્યાનમાં લેતા) સમાન હશે.₁+φ₂+φ₃+φ₄+φ₅+...φ_n;
• જો ચાર્જથી અંતર એવું હોય કે ચાર્જિસને પોઈન્ટ-જેવા ગણી શકાય, તો કુલ સંભવિતની ગણતરી સૂત્ર φ=k*(q₁/આર₁+q₂/આર₂+q₃/આર₃+...q_n/આર_n), જ્યાં r એ સંબંધિત ચાર્જથી પ્રશ્નાર્થ બિંદુ સુધીનું અંતર છે.

જો ક્ષેત્ર ઇલેક્ટ્રિક દ્વિધ્રુવ (વિરોધી ચિહ્નના બે જોડાયેલા ચાર્જ) દ્વારા રચાય છે, તો દ્વિધ્રુવથી r ના અંતરે સ્થિત કોઈપણ બિંદુ પર સંભવિત φ=k*p*cosά/r બરાબર હશે.², ક્યાં:

• p એ દ્વિધ્રુવનો ઇલેક્ટ્રિક હાથ છે, જે q*l ની બરાબર છે, જ્યાં l એ ચાર્જ વચ્ચેનું અંતર છે;
• r એ દ્વિધ્રુવનું અંતર છે;
• ά એ દ્વિધ્રુવ હાથ અને ત્રિજ્યા વેક્ટર r વચ્ચેનો ખૂણો છે.

જો બિંદુ દ્વિધ્રુવ ધરી પર આવેલું હોય, તો cosά=1 અને φ=k*p/r².

સંભવિત તફાવત

જો બે બિંદુઓમાં ચોક્કસ સંભવિત હોય, અને જો તે સમાન ન હોય, તો એવું કહેવાય છે કે બે બિંદુઓ વચ્ચે સંભવિત તફાવત છે. પોઈન્ટ વચ્ચે સંભવિત તફાવત જોવા મળે છે:

• જેની સંભવિતતા વિવિધ ચિહ્નોના શુલ્ક દ્વારા નક્કી કરવામાં આવે છે;
• કોઈપણ ચિહ્નના ચાર્જમાંથી સંભવિત સાથેનો બિંદુ અને શૂન્ય સંભવિત સાથેનો બિંદુ;
• સમાન ચિહ્નની સંભવિતતા ધરાવતા બિંદુઓ, પરંતુ મોડ્યુલોમાં અલગ.

એટલે કે, સંભવિત તફાવત સંકલન પ્રણાલીની પસંદગી પર આધારિત નથી. આપણે શૂન્ય ચિહ્ન (દા.ત. દરિયાની સપાટી)ની તુલનામાં જુદી જુદી ઊંચાઈએ સ્થિત પાણીના પૂલ સાથે સામ્યતા દોરી શકીએ છીએ.

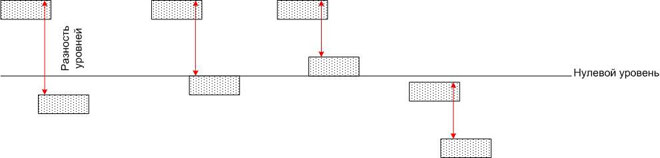
દરેક પૂલના પાણીમાં ચોક્કસ સંભવિત ઉર્જા હોય છે, પરંતુ જો તમે બે કોઈપણ પૂલને ટ્યુબ વડે જોડો છો, તો તેમાંથી દરેકમાં પાણીનો પ્રવાહ હશે, જેનો પ્રવાહ માત્ર નળીના કદ દ્વારા જ નક્કી થતો નથી, પણ પૃથ્વીના ગુરુત્વાકર્ષણ ક્ષેત્રમાં સંભવિત ઊર્જાના તફાવત દ્વારા (એટલે ​​​​કે, ઊંચાઈનો તફાવત). સંભવિત ઉર્જાઓનું સંપૂર્ણ મૂલ્ય આ કિસ્સામાં વાંધો નથી.

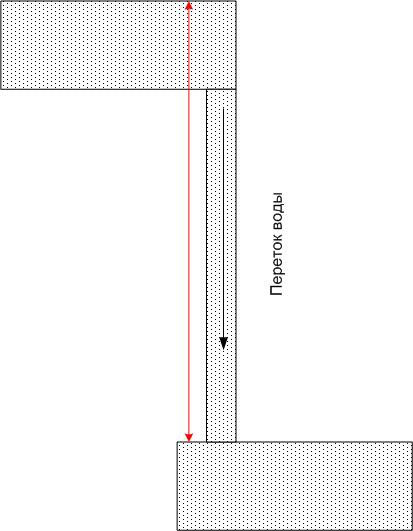
તેવી જ રીતે, જો તમે વાહકને અલગ-અલગ સંભવિતતાવાળા બે બિંદુઓ સાથે જોડો છો, તો તે વહન કરશે ઇલેક્ટ્રિક પ્રવાહમાત્ર કંડક્ટરના પ્રતિકાર દ્વારા જ નહીં, પણ સંભવિત તફાવત દ્વારા પણ નક્કી કરવામાં આવે છે (પરંતુ તેમના સંપૂર્ણ મૂલ્ય દ્વારા નહીં). પાણીની સામ્યતા સાથે ચાલુ રાખીને, આપણે કહી શકીએ કે ઉપલા બેસિનમાંનું પાણી ટૂંક સમયમાં સમાપ્ત થઈ જશે, અને જો પાણીને પાછું ઉપર ખસેડવા માટે કોઈ બળ ન હોય (જેમ કે પંપ), તો પ્રવાહ ખૂબ જ ઝડપથી બંધ થઈ જશે.

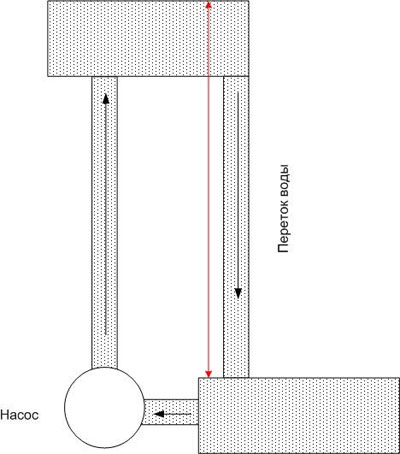
વિદ્યુત સર્કિટમાં તે સમાન છે: સંભવિત તફાવતને ચોક્કસ સ્તરે રાખવા માટે, એક બળ જરૂરી છે જે ચાર્જ (અથવા તેના બદલે, ચાર્જ કેરિયર્સ) ને ઉચ્ચતમ સંભવિતતાવાળા બિંદુ સુધી પરિવહન કરે છે. આ બળને ઇલેક્ટ્રોમોટિવ બળ કહેવામાં આવે છે અને તેને EMF તરીકે સંક્ષિપ્ત કરવામાં આવે છે. EMF વિવિધ પ્રકૃતિના હોઈ શકે છે - ઇલેક્ટ્રોકેમિકલ, ઇલેક્ટ્રોમેગ્નેટિક, વગેરે.

વ્યવહારમાં, તે મુખ્યત્વે ચાર્જ કેરિયર્સના માર્ગના પ્રારંભ અને અંતિમ બિંદુઓ વચ્ચેનો સંભવિત તફાવત છે જે મહત્વપૂર્ણ છે. આ કિસ્સામાં, આ તફાવતને વોલ્ટેજ કહેવામાં આવે છે, અને SI માં તે વોલ્ટ્સમાં પણ માપવામાં આવે છે. 1 વોલ્ટના વોલ્ટેજની વાત કરી શકાય છે જો ક્ષેત્ર 1 કૂલમ્બના ચાર્જને એક બિંદુથી બીજા સ્થાને ખસેડવામાં 1 જૌલનું કામ કરે છે, એટલે કે, 1V=1J/1KL, અને J/KL પણ એકમ હોઈ શકે છે. સંભવિત તફાવત.

ઇક્વિપોટેન્શિયલ સપાટીઓ

જો અનેક બિંદુઓની સંભવિતતા સમાન હોય, અને આ બિંદુઓ સપાટી બનાવે છે, તો આવી સપાટીને ઇક્વિપોટેન્શિયલ કહેવામાં આવે છે. ઉદાહરણ તરીકે, ઈલેક્ટ્રિક ચાર્જની આસપાસના ગોળામાં આ ગુણધર્મ હોય છે, કારણ કે વિદ્યુત ક્ષેત્ર અંતર સાથે તમામ દિશામાં સમાન રીતે ઘટે છે.

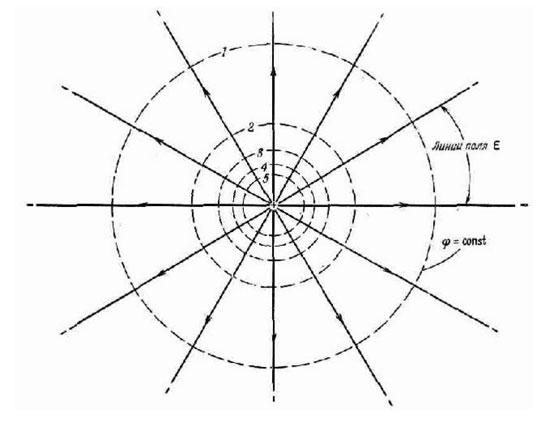
આ સપાટી પરના તમામ બિંદુઓ સમાન સંભવિત ઉર્જા ધરાવે છે, તેથી આવા ગોળા પર ચાર્જ ખસેડતી વખતે કોઈ કાર્ય ખર્ચવામાં આવશે નહીં. અનેક ચાર્જની સિસ્ટમોની ઇક્વિપોટેન્શિયલ સપાટીઓ વધુ જટિલ આકાર ધરાવે છે, પરંતુ તેમની પાસે એક રસપ્રદ ગુણધર્મ છે: તેઓ ક્યારેય છેદે નથી. વિદ્યુત ક્ષેત્રના બળની રેખાઓ તેમના દરેક બિંદુઓ પર સમાન સંભવિત સાથેની સપાટીઓ પર હંમેશા લંબરૂપ હોય છે. જો સમકક્ષ સપાટીને પ્લેન દ્વારા વિચ્છેદ કરવામાં આવે છે, તો તમને સમાન સંભવિતતાની રેખા મળે છે.તે સમકક્ષ સપાટી જેવા જ ગુણધર્મો ધરાવે છે. વ્યવહારમાં, ઇલેક્ટ્રોસ્ટેટિક ક્ષેત્રમાં મૂકવામાં આવેલા વાહકની સપાટી પરના બિંદુઓ, ઉદાહરણ તરીકે, સમાન સંભવિતતા ધરાવે છે.

એકવાર તમે સંભવિત અને સંભવિત તફાવતનો ખ્યાલ સમજી લો, પછી તમે વિદ્યુત ઘટનાનો વધુ અભ્યાસ કરવાનું શરૂ કરી શકો છો. પરંતુ પહેલાં નહીં, કારણ કે મૂળભૂત સિદ્ધાંતો અને ખ્યાલોને સમજ્યા વિના જ્ઞાનને વધુ ઊંડું કરવું શક્ય બનશે નહીં.

સંબંધિત લેખો: