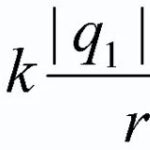Koncept električnega potenciala je eden od pomembnih temeljev teorije elektrostatike in elektrodinamike. Razumevanje njegovega bistva je predpogoj za nadaljnji študij teh delov fizike.
Vsebina
Kaj je električni potencial
Naj bo enota naboja q postavljena v polje, ki ga ustvarja stacionarni naboj Q, na katerem je Coulombova sila F=k*Qq/r.
V nadaljevanju k=((1/4)*π* ε* ε), kjer je ε0 — je električna konstanta (8,85*10-12 F/m) in ε dielektrična konstanta medija.
Predstavil napolniti pod delovanjem te sile se lahko premika in sila bo opravila neko delo. To pomeni, da ima sistem dveh nabojev potencialno energijo, ki je odvisna od velikosti obeh nabojev in razdalje med njima, vrednost te potencialne energije pa ni odvisna od velikosti naboja q. Tu je uvedena definicija električnega potenciala: enaka je razmerju med potencialno energijo polja in velikostjo naboja:
φ=W/q,
kjer je W potencialna energija polja, ki ga ustvarja sistem nabojev, potencial pa je energetska značilnost polja. Za premikanje naboja q v električnem polju za določeno razdaljo je potrebno porabiti nekaj dela za premagovanje Coulombove sile.Potencial točke je enak delu, ki je potrebno za premik enote naboja iz te točke v neskončnost. Opozoriti je treba, da:
- to delo bo enako izgubi potencialne energije naboja (A=W2-W1);
- delo ni odvisno od trajektorije naboja.
V sistemu SI je enota potenciala en volt (označen z V v literaturi v ruskem jeziku, V v tuji literaturi). 1 V=1J/1 Kl, kar pomeni, da lahko govorimo o potencialu točke 1 Volta, če je potrebno delo 1 Joula, da se naboj 1 Kl premakne v neskončnost. Ime je bilo izbrano v čast italijanskemu fiziku Alessandru Volti, ki je pomembno prispeval k razvoju elektrotehnike.
Da bi vizualizirali, kaj je potencial, ga lahko primerjamo s temperaturo dveh teles ali temperaturo, izmerjeno na različnih točkah v vesolju. Temperatura je merilo za segrevanje predmetov, potencial pa je merilo za električni naboj. Za eno telo pravimo, da je bolj segreto kot drugo, lahko pa tudi rečemo, da je eno telo bolj in drugo manj naelektreno. Ta telesa imajo različne potenciale.
Vrednost potenciala je odvisna od izbire koordinatnega sistema, zato je treba neko raven vzeti za nič. Pri merjenju temperature bi lahko kot referenčno mejo vzeli na primer temperaturo talečega se ledu. Za potencial je običajno enak nič potencial neskončno oddaljene točke, pri nekaterih problemih pa lahko za nič vzamemo na primer potencial zemlje ali potencial enega od pokrovov kondenzatorja.
Lastnosti potencialov
Med pomembnimi lastnostmi potenciala so naslednje:
- če polje ustvari več nabojev, bo potencial na določeni točki enak algebraični (ob upoštevanju predznaka naboja) vsoti potencialov, ki jih ustvari vsak od nabojev φ=φ1+φ2+φ3+φ4+φ5+...+φn;
- če so razdalje od nabojev takšne, da se sami naboji lahko obravnavajo kot točkasti, se skupni potencial izračuna po formuli φ=k*(q1/r1+q2/r2+q3/r3+...+qn/rn), kjer je r razdalja od ustreznega naboja do zadevne točke.
Če polje tvori električni dipol (dva povezana naboja nasprotnega predznaka), bo potencial na kateri koli točki, ki se nahaja na razdalji r od dipola, enak φ=k*p*cosά/r2, kje:
- p je električni krak dipola, enak q*l, kjer je l razdalja med naboji;
- r razdalja do dipola;
- ά je kot med krakom dipola in radijskim vektorjem r.
Če točka leži na osi dipola, je cosά=1 in φ=k*p/r2.
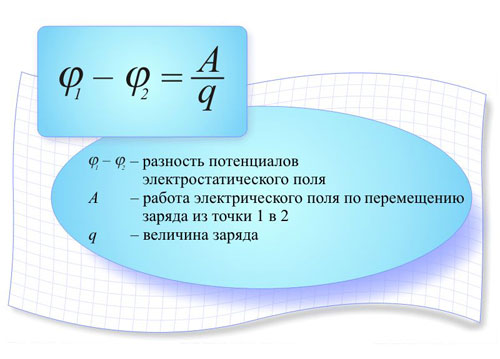
Potencialna razlika
Če imata dve točki določen potencial in če nista enaka, pravimo, da obstaja potencialna razlika med točkama. Med točkami se pojavi potencialna razlika:
- katerih potencial je določen z naboji različnih predznakov;
- točka s potencialom iz naboja katerega koli predznaka in točka z nič potencialom;
- točke, ki imajo potencial enakega predznaka, vendar različne po modulu.
To pomeni, da potencialna razlika ni odvisna od izbire koordinatnega sistema. Lahko potegnemo analogijo z bazeni vode, ki se nahajajo na različnih višinah glede na ničelno oznako (npr. gladina morja).
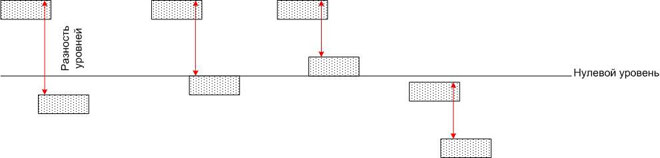
Voda vsakega bazena ima določeno potencialno energijo, toda če dva poljubna bazena povežete s cevjo, potem bo v vsakem od njih potekal tok vode, katerega pretok ni določen le z velikostjo cevi, ampak tudi z velikostjo cevi. ampak tudi z razliko potencialnih energij v gravitacijskem polju Zemlje (to je razlika višin). Absolutna vrednost potencialnih energij v tem primeru ni pomembna.
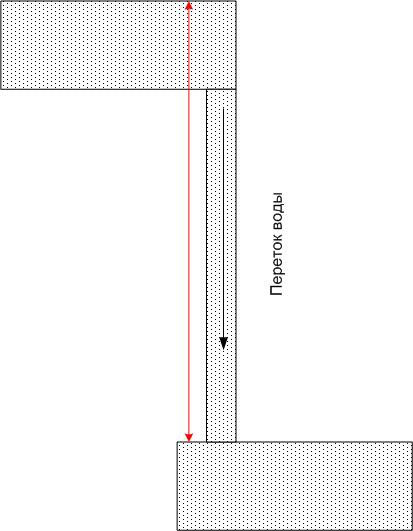
Podobno, če priključite prevodnik na dve točki z različnimi potenciali, bo prenašal električni tokdoločena ne le z uporom prevodnika, temveč tudi s potencialno razliko (vendar ne z njihovo absolutno vrednostjo). Če nadaljujemo z vodno analogijo, lahko rečemo, da bo vode v zgornjem bazenu kmalu zmanjkalo, in če ni sile, ki bi vodo premaknila nazaj navzgor (kot je črpalka), se bo tok zelo hitro ustavil.
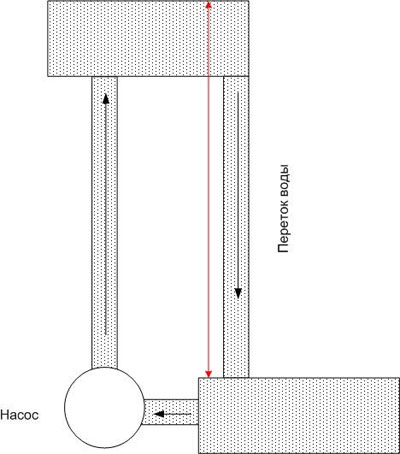
Enako je v električnem tokokrogu: za ohranjanje potencialne razlike na določeni ravni je potrebna sila, ki prenaša naboje (ali bolje rečeno nosilce naboja) do točke z največjim potencialom. To silo imenujemo elektromotorna sila in jo skrajšano imenujemo EMF. EMF je lahko različne narave - elektrokemična, elektromagnetna itd.
V praksi je pomembna predvsem potencialna razlika med začetno in končno točko trajektorije nosilcev naboja. V tem primeru se ta razlika imenuje napetost, v SI pa se meri tudi v voltih. O napetosti 1 volta lahko govorimo, če polje opravi delo 1 joula pri premikanju naboja 1 kulona iz ene točke v drugo, to je 1V=1J/1KL, J/KL pa je lahko tudi enota potencialna razlika.
Ekvipotencialne površine
Če je potencial več točk enak in te točke tvorijo površino, se taka površina imenuje ekvipotencialna. To lastnost ima na primer krogla, ki je obdana z električnim nabojem, ker se električno polje z razdaljo enakomerno zmanjšuje v vseh smereh.
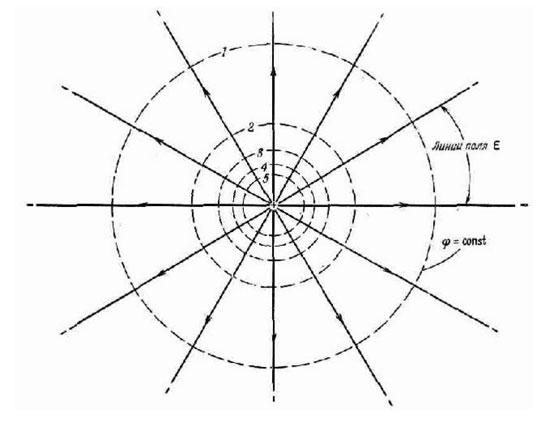
Vse točke na tej površini imajo enako potencialno energijo, zato pri premikanju naboja na takšni krogli ne bo porabljenega dela. Ekvipotencialne površine sistemov z več naboji imajo bolj zapleteno obliko, vendar imajo eno zanimivo lastnost: nikoli se ne sekajo. Silnice električnega polja so vedno pravokotne na površine z enakim potencialom v vsaki svoji točki. Če ekvipotencialno ploskev presekamo z ravnino, dobimo črto enakih potencialov.Ima enake lastnosti kot ekvipotencialna površina. V praksi imajo na primer točke na površini prevodnika, postavljenega v elektrostatično polje, enak potencial.
Ko razumete koncept potenciala in potencialne razlike, lahko začnete nadalje preučevati električne pojave. Vendar ne prej, saj brez razumevanja osnovnih principov in pojmov poglabljanje znanja ne bo mogoče.
Povezani članki: