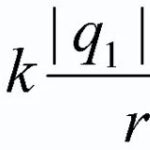A força de Lorentz e a regra da mão esquerda. Movimento de partículas carregadas num campo magnético

Um condutor colocado num campo magnético maestroatravés da qual uma corrente eléctrica uma corrente eléctricaé afectado pela força Ampere $F_A$ e a sua magnitude pode ser calculada através da seguinte fórmula

$F_A=B=B\cdot I\cdot l\cdot l\cdot sinpha$ (1)

onde $I$ и $l$ - amperagem e comprimento do condutor, $B$ - a indução do campo magnético, $\alfa$ - o ângulo entre as direcções da corrente e a indução magnética. Então porque é que isto está a acontecer?

Lorentz force. Movimento de uma partícula carregada num campo magnético.

Conteúdos

1 O que é a força de Lorentz - definição, quando ocorre, obter a fórmula
2 Determinação da direcção da força de Lorentz utilizando a regra da mão esquerda
3 Movimento de uma partícula carregada num campo magnético
4 Aplicação da força de Lorentz na engenharia

Qual é a força de Lorentz - definição, quando surge, derivando a fórmula

É sabido que a corrente eléctrica é o movimento ordenado das partículas carregadas. Sabe-se também que ao mover-se num campo magnético, cada uma destas partículas está sujeita a uma força. Para que uma força ocorra, uma partícula deve estar em movimento.

A força de Lorentz é a força que actua sobre uma partícula carregada electricamente à medida que se move num campo magnético. A sua direcção é ortogonal ao plano em que se encontram os vectores de velocidade da partícula e a força do campo magnético. A força de Lorentz é a força Ampere. Conhecendo-a, a fórmula para a força de Lorentz pode ser derivada.

O tempo necessário para que uma partícula atravesse uma secção de um condutor, $t = \frac {l}{v}$ onde $l$ - é o comprimento do segmento, $v$ - velocidade da partícula. A carga total transportada durante este tempo através da secção transversal do condutor, $Q = I\cdot t$ . Substituindo aqui o valor do tempo da equação anterior, temos

$Q = {I=frac l}{v}$ (2)

Ao mesmo tempo $F_A = F_L\cdot N$ onde $N$ - é o número de partículas no condutor considerado. Ao mesmo tempo $N = \frac {Q}{q}$ onde $q$ - é a carga de uma partícula. Substituindo em fórmula $Q$ a partir de (2), pode-se obter:

$N = {I=frac {v=cdot l}{v=cdot q}$

Assim,

$F_A=F_L\cdot {I\cdot l}{v\cdot q}$

Usando (1), a expressão anterior pode ser escrita como

$B{\i1}b_cdot I{\i1}cdot l{\i1}cdot l{\i}cdot sinpha = F_L{\i}frac {\i}{v{\i}cdot l{\i}$

Após cortes e transferências obtemos a fórmula para o cálculo da força de Lorentz

$F_L = q\cdot v\cdot B\cdot sinpha$

Dado que a fórmula é escrita para um módulo de força, deve ser escrita como se segue:

$F_L = |q||||cdot v=cdot B=cdot sin=alpha$ (3)

Desde $sin\alpha = sin(180^{\circ} - {\alpha)$ , não importa para o cálculo do módulo Lorentz se a velocidade está na direcção da corrente ou contra ela, e podemos dizer que $\alfa$ - é o ângulo formado pelos vectores de velocidade da partícula e a indução magnética.

Escrever a fórmula em forma vectorial terá este aspecto:

$\q=vec{F_L} = q=cdot [q=vec{vec{vec{vec{B}] vezes]$

$[vec{vec{vec{b}] vezes]$ - é o produto vectorial, cujo resultado é um vector com módulo igual a $v\cdot B\cdot sinpha$ .

Da fórmula (3) podemos concluir que a força de Lorentz é máxima no caso da perpendicularidade das direcções da corrente eléctrica e do campo magnético, ou seja, em $\alfa = 90^{\i1}circ$ e desaparecerá no seu paralelismo ( $\0^^ Cir$ ).

Deve-se lembrar que, para dar uma resposta quantitativa correcta - por exemplo, na resolução de problemas - deve-se utilizar unidades SI, nas quais a indução magnética é medida em teslas (1 Tesla = 1 kg-c⁻²-А⁻¹), força em newton (1 N = 1 kg-m/s²), corrente em amperes, carga em coulons (1 Cl = 1 A-s), comprimento em metros, velocidade em m/s.

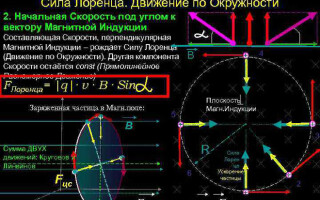
Determinação da direcção da força de Lorentz utilizando a regra da esquerda

Uma vez que no mundo dos macro objectos a força de Lorentz se manifesta como uma força Ampere, podemos usar a regra da esquerda para encontrar a sua direcção.

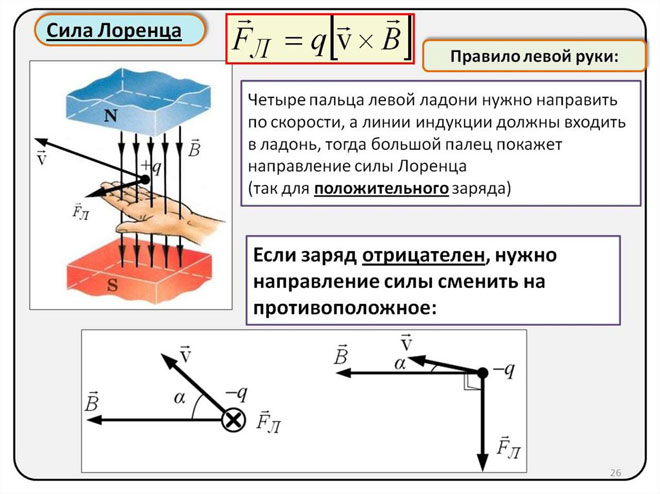
Determinar a direcção da força de Lorentz utilizando a regra da mão esquerda.

Com a mão esquerda posicionada perpendicularmente e virada para as linhas do campo magnético, os quatro dedos devem ser estendidos na direcção da corrente, depois a força de Lorentz será dirigida para onde o polegar, que deve ser dobrado, aponta.

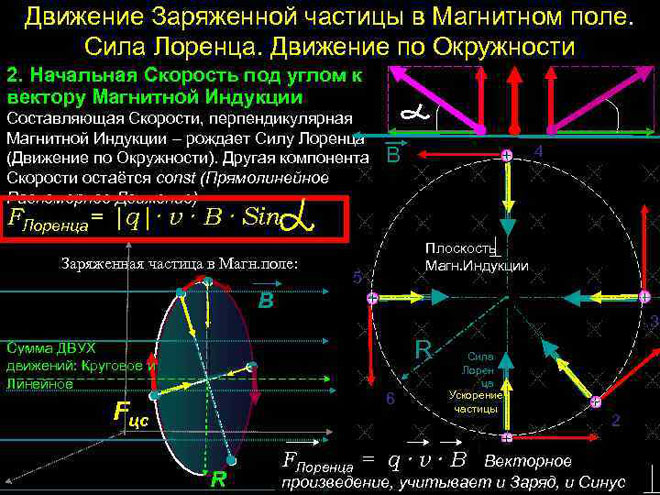
Movimento de uma partícula carregada num campo magnético

No caso mais simples, isto é, com ortogonalidade dos vectores de indução magnética e velocidade da partícula, sendo a força de Lorentz perpendicular ao vector de velocidade, só pode alterar a sua direcção. A magnitude da velocidade, portanto, a energia permanecerá inalterada. Assim, a força de Lorentz actua por analogia à força centrípeta na mecânica e a partícula move-se num círculo.

De acordo com a segunda lei de Newton ( $F = m\cdot a$ ) é possível determinar o raio de rotação de uma partícula:

$N = {mcdot v}{q=cdot B}$ .

Deve-se notar que, como a carga específica da partícula muda ( $\frac {q}{m}$ ) o raio também muda.

Assim, o período de rotação T = . $\frac {2cdot r}{v}$ = $\frac {2}frac {2}cdot m$ . Não depende da velocidade, pelo que a posição mútua das partículas com velocidades diferentes será a mesma.

O movimento de uma partícula carregada num campo magnético homogéneo.

No caso mais complicado, quando o ângulo entre a velocidade da partícula e a força do campo magnético é arbitrário, deslocar-se-á ao longo de uma trajectória helicoidal - progressivamente à custa da componente de velocidade dirigida paralelamente ao campo, e circunferencialmente à influência da sua componente perpendicular.

Aplicações da força de Lorentz na engenharia

Cinescópio

O cinescópio, que até recentemente, quando foi substituído pelo LCD (ecrã plano), estava em todos os aparelhos de televisão, não poderia ter funcionado sem a força de Lorentz. Para formar uma imagem de televisão no ecrã, um fluxo estreito de electrões são bobinas deflectoras que geram um campo magnético linearmente variável. As bobinas de linha movem o feixe de electrões da esquerda para a direita e para trás, enquanto as bobinas de estrutura são responsáveis pelo movimento vertical, movendo o feixe de corrida horizontalmente de cima para baixo. O mesmo princípio é utilizado em osciloscópios - instrumentos utilizados para estudar as tensões eléctricas alternadas.

Espectrógrafo de massa

Um espectrógrafo de massa é um instrumento que utiliza a relação entre o raio de rotação de uma partícula carregada e a sua carga específica. O seu princípio de funcionamento é o seguinte:

Uma fonte de partículas carregadas, que ganham velocidade por meio de um campo eléctrico criado artificialmente, é colocada numa câmara de vácuo para eliminar a influência das moléculas do ar. As partículas voam para fora da fonte e, seguindo um arco de círculo, atingem uma placa fotográfica, deixando vestígios na mesma. Dependendo da carga específica, o raio de trajectória e, portanto, o ponto de impacto muda. Este raio é fácil de medir e, sabendo-o, a massa da partícula pode ser calculada. Utilizando um espectrógrafo de massa, por exemplo, foi estudada a composição do solo lunar.

Cyclotron

A independência do período e, por conseguinte, a velocidade de uma partícula carregada em relação à sua velocidade na presença de um campo magnético é utilizada num aparelho chamado ciclotrão, que é concebido para acelerar as partículas a alta velocidade. O ciclotrão é composto por dois meios cilindros ocos de metal, duants (cada uma com o formato de uma letra D latina), colocados com os seus lados direitos virados um para o outro a uma curta distância.

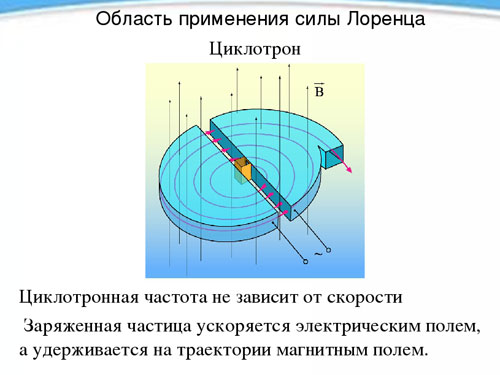
Cyclotron - aplicação da força de Lorentz.

Os duants são colocados num campo magnético homogéneo constante, e é criado entre eles um campo eléctrico alternado, cuja frequência é igual à frequência de rotação da partícula, determinada pela força do campo magnético e pela carga específica. Sendo influenciada pelo campo eléctrico duas vezes durante o período de rotação (ao passar de um duant para outro), a partícula é acelerada de cada vez, aumentando assim o raio de trajectória, e num determinado momento, tendo ganho a velocidade necessária, voa para fora do dispositivo através do buraco. Desta forma, pode-se acelerar um próton para uma energia de 20 MeVmega electrão-volt).

Magnetron

Um dispositivo chamado magnetrão, que é instalado em cada forno microondasé outro exemplo de um aparelho que funciona utilizando a força de Lorentz. O magnetrão cria um forte campo de microondas que aquece o volume interno do forno em que os alimentos são colocados. Os ímanes no magnetrão ajustam o caminho dos electrões no interior do forno.

O campo magnético da Terra

Na natureza, a força de Lorentz é muito importante para a humanidade. A sua presença permite que o campo magnético da Terra proteja os seres humanos da radiação ionizante mortal do espaço. O campo impede as partículas carregadas de bombardear a superfície do planeta, forçando-as a mudar de direcção.