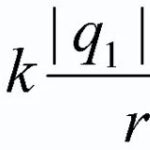Lorenca spēks un kreisās rokas likums. Uzlādētu daļiņu kustība magnētiskajā laukā

Magnētiskā laukā novietots vadītsvins diriģentscaur kuru plūst elektriskā strāva elektriskā strāvaietekmē Ampera spēks $F_A$ , un tās lielumu var aprēķināt pēc šādas formulas

$F_A=B\cdot I\cdot l\cdot sin\alfa$ (1)

kur $I$ и $l$ - strāvas stiprums un vadītāja garums, $B$ - magnētiskā lauka indukcija, $\alfa$ - leņķis starp strāvas un magnētiskās indukcijas virzieniem. Kāpēc tas notiek?

Lorenca spēks. Uzlādētas daļiņas kustība magnētiskajā laukā.

Saturs

1 Kas ir Lorenca spēks - definīcija, kad tas rodas, iegūstot formulu
2 Lorenca spēka virziena noteikšana, izmantojot kreisās rokas noteikumu
3 lādētas daļiņas kustība magnētiskajā laukā
4 Lorenca spēka pielietošana inženierzinātnēs

Kas ir Lorenca spēks - definīcija, kad tas rodas, atvasinot formulu

Ir zināms, ka elektriskā strāva ir sakārtota lādētu daļiņu kustība. Ir arī zināms, ka, pārvietojoties magnētiskajā laukā, uz katru no šīm daļiņām iedarbojas spēks. Lai radītu spēku, daļiņai ir jābūt kustībā.

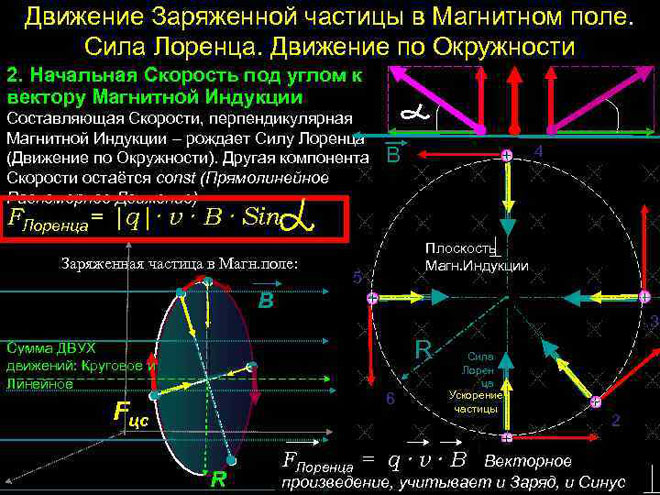
Lorenca spēks ir spēks, kas iedarbojas uz elektriski lādētu daļiņu, kad tā pārvietojas magnētiskajā laukā. Tās virziens ir perpendikulārs plaknei, kurā atrodas daļiņas ātruma vektori un magnētiskā lauka intensitāte. Lorenca spēks ir Ampera spēks. To zinot, var iegūt Lorenca spēka formulu.

Laiks, kas nepieciešams, lai daļiņa šķērsotu kādu vadītāja posmu, $t = \frac {l}{v}$ kur $l$ - ir segmenta garums, $v$ - daļiņas ātrums. Kopējais lādiņš, kas šajā laikā tiek pārnests caur vadītāja šķērsgriezumu, $Q = I\cdot t$ . Ievietojot šeit laika vērtību no iepriekšējā vienādojuma, iegūstam šādu formulu

$Q = \frac {I\cdot l}{v}$ (2)

Tajā pašā laikā $F_A = F_L\\cdot N$ kur $N$ - ir daļiņu skaits attiecīgajā vadītājā. Tajā pašā laikā $N = \frac {Q}{q}$ kur $q$ - ir vienas daļiņas lādiņš. Ievietojot formulā $Q$ no (2) var iegūt:

$N = \frac {I\cdot l}{v\cdot q}$

Tādējādi,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Izmantojot (1), iepriekšējo izteiksmi var aizrakstīt šādi.

$B\cdot I\cdot l\cdot sin\alfa = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Pēc griezumiem un pārnesumiem iegūstam Lorenca spēka aprēķina formulu

$F_L = q\cdot v\cdot B\cdot sin\alfa$

Ņemot vērā, ka formula ir rakstīta spēka modulim, tā ir jāraksta šādi:

Lasiet arī: Kā pārvērst ampērus vatos un atpakaļ?

$F_L = |q||\cdot v\cdot B\cdot sin\alfa$ (3)

Tā kā $sin\alfa = sin(180^{\circ} - \alfa)$ , Lorenca moduļa aprēķināšanai nav nozīmes, vai ātrums ir strāvas virzienā vai pret to, un mēs varam teikt, ka $\alfa$ - ir leņķis, ko veido daļiņas ātruma vektori un magnētiskā indukcija.

Formulas ierakstīšana vektora formā izskatīsies šādi:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}].$

$[\vec{v}\ reizes \vec{B}]$ - ir vektora reizinājums, kura rezultātā iegūst vektoru ar moduli, kas vienāds ar $v\cdot B\cdot sin\alfa$ .

No (3) formulas var secināt, ka Lorenca spēks ir maksimāls gadījumā, ja elektriskās strāvas un magnētiskā lauka virzieni ir perpendikulāri, t.i., pie. $\alpha = 90^{\circ}$ un pazudīs pie to paralēlisma ( $\alpha = 0^{\\circ}$ ).

Jāatceras, ka, lai sniegtu pareizu kvantitatīvu atbildi, piemēram, risinot uzdevumus, jāizmanto SI vienības, kurās magnētisko indukciju mēra teslās (1 Tesla = 1 kg-c).⁻²-А⁻¹), spēks ņūtonos (1 N = 1 kg-m/s²), strāva ampēros, lādiņš kulonos (1 Cl = 1 A-s), garums metros, ātrums m/s.

Lorenca spēka virziena noteikšana, izmantojot kreisās rokas noteikumu

Tā kā makroobjektu pasaulē Lorenca spēks izpaužas kā Ampera spēks, mēs varam izmantot kreisās rokas noteikumu, lai noteiktu tā virzienu.

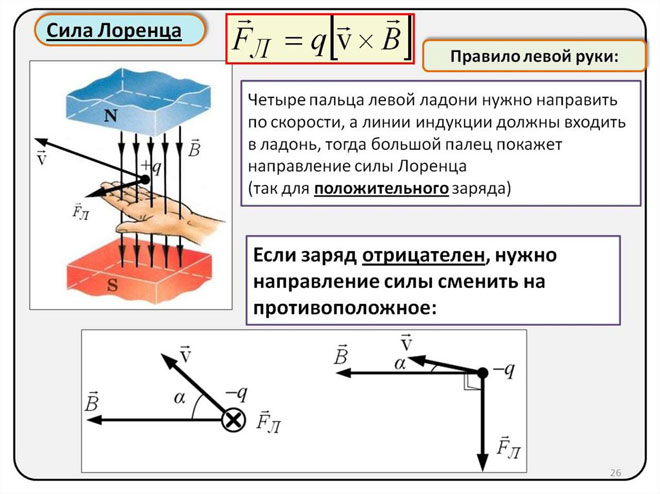
Lorenca spēka virziena noteikšana, izmantojot kreisās rokas noteikumu.

Ja kreisā roka ir novietota perpendikulāri magnētiskā lauka līnijām un vērsta pret tām, tad četriem pirkstiem jābūt izstieptiem strāvas virzienā, tad Lorenca spēks būs vērsts uz to vietu, uz kuru norāda īkšķis, kuram jābūt saliektam.

lādētas daļiņas kustība magnētiskajā laukā

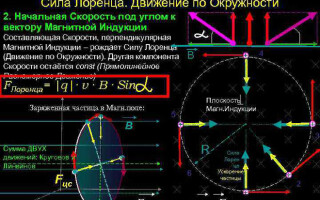
Vienkāršākajā gadījumā, t. i., ja magnētiskās indukcijas un daļiņas ātruma vektoru ortogonālitāte ir perpendikulāra ātruma vektoram, Lorenca spēks, kas ir perpendikulārs ātruma vektoram, var mainīt tikai tā virzienu. Ātruma lielums, tātad arī enerģija nemainīsies. Tātad Lorenca spēks darbojas pēc analoģijas ar centripetālo spēku mehānikā, un daļiņa pārvietojas pa apli.

Lasiet arī: Cik vatu ir kilovatā?

Saskaņā ar Ņūtona otro likumu ( $F = m\cdot a$ ) var noteikt daļiņas rotācijas rādiusu:

$N = \frac {m\cdot v}{q\cdot B}$ .

Jāatzīmē, ka, mainoties daļiņas īpatnējam lādiņam ( $\frac {q}{m}$ ) mainās arī rādiuss.

Tādējādi rotācijas periods T = . $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Tas nav atkarīgs no ātruma, tāpēc daļiņu ar dažādiem ātrumiem savstarpējā atrašanās vieta būs vienāda.

lādētas daļiņas kustība homogēnā magnētiskajā laukā.

Sarežģītākā gadījumā, kad leņķis starp daļiņas ātrumu un magnētiskā lauka intensitāti ir patvaļīgs, tā virzīsies pa spirālveida trajektoriju - pakāpeniski uz laukam paralēlās ātruma komponentes rēķina un pa apli uz tās perpendikulārās komponentes rēķina.

Lorenca spēka pielietojums inženierzinātnēs

Kineskops

Kineskops, kas vēl nesen, kad to nomainīja LCD (plakanā ekrāna) ekrāns, bija katrā televizorā, nevarēja darboties bez Lorenca spēka. Lai uz ekrāna veidotu televīzijas attēlu, šauras elektronu plūsmas ir deflektora spoles, kas rada lineāri mainīgu magnētisko lauku. Lineārās spoles virza elektronu staru kūli no kreisās puses uz labo un atpakaļ, bet rāmja spoles ir atbildīgas par vertikālo kustību, virzot elektronu staru horizontāli no augšas uz leju. Tas pats princips tiek izmantots osciloskopi - instrumenti, ko izmanto, lai pētītu maiņstrāvas spriegumu.

Masas spektrogrāfs

Masas spektrogrāfs ir instruments, kas izmanto sakarību starp lādētas daļiņas rotācijas rādiusu un tās īpatnējo lādiņu. Tās darbības princips ir šāds:

Lai novērstu gaisa molekulu ietekmi, vakuuma kamerā ievieto lādētu daļiņu avotu, kas mākslīgi radītā elektriskā lauka ietekmē iegūst ātrumu. Daļiņas izlido no avota un, sekojot apļa lokam, nokļūst uz fotoplates, atstājot uz tās pēdas. Atkarībā no konkrētā lādiņa mainās trajektorijas rādiuss un līdz ar to arī trieciena punkts. Šo rādiusu ir viegli izmērīt, un, zinot to, var aprēķināt daļiņas masu. Piemēram, izmantojot masas spektrogrāfu, ir izpētīts Mēness augsnes sastāvs.

Lasiet arī: Kādas profesijas ir saistītas ar elektrību

Ciklotrons

Uzlādētas daļiņas perioda un līdz ar to rotācijas frekvences neatkarība no tās ātruma magnētiskā lauka klātbūtnē tiek izmantota aparātā, ko sauc par ciklotronu un kas paredzēts daļiņu paātrināšanai līdz lieliem ātrumiem. Ciklotrons sastāv no diviem dobiem metāla puscilindriem, duantiem (katrs no tiem ir latīņu burta D formā.), kas novietoti ar taisnajām malām viens pret otru nelielā attālumā.

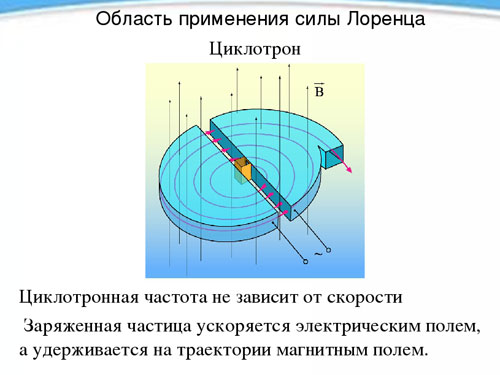
Ciklotrons - Lorenca spēka pielietojums.

Duanti tiek novietoti pastāvīgā homogēnā magnētiskajā laukā, un starp tiem tiek radīts mainīgs elektriskais lauks, kura frekvence ir vienāda ar daļiņas rotācijas frekvenci, ko nosaka magnētiskā lauka intensitāte un īpatnējais lādiņš. Tā kā rotācijas laikā (pārejot no viena duanta uz otru) uz daļiņu divreiz iedarbojas elektriskais lauks, tā katru reizi tiek paātrināta, tādējādi palielinot trajektorijas rādiusu, un noteiktā brīdī, uzkrājusi vajadzīgo ātrumu, tā izlec no ierīces caur caurumu. Šādā veidā var paātrināt protonu līdz 20 MeV enerģijai.megaelektronvolts).

Magnetrons

Ierīce, ko sauc par magnetronu un kas ir uzstādīta katrā mikroviļņu krāsnsir vēl viens piemērs ierīcei, kas darbojas, izmantojot Lorenca spēku. Magnetrons rada spēcīgu mikroviļņu lauku, kas uzkarsē cepeškrāsns iekšējo tilpumu, kurā tiek ievietots ēdiens. Magnēti magnetronā regulē elektronu ceļu krāsnī.

Zemes magnētiskais lauks

Dabā Lorenca spēks ir ļoti svarīgs cilvēcei. Tās klātbūtne ļauj Zemes magnētiskajam laukam pasargāt cilvēkus no nāvējošā jonizējošā starojuma kosmosā. Lauks neļauj lādētām daļiņām bombardēt planētas virsmu, liekot tām mainīt virzienu.

Saistītie raksti: