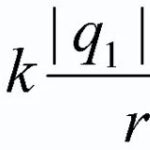La forza di Lorentz e la regola della mano sinistra. Movimento di particelle cariche in un campo magnetico

Un conduttore posto in un campo magnetico conduttoreattraverso il quale una corrente elettrica una corrente elettricaè influenzato dalla forza di Ampere $F_A$ e la sua grandezza può essere calcolata con la seguente formula

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

dove $I$ и $l$ - amperaggio e lunghezza del conduttore, $B$ - l'induzione del campo magnetico, $\alpha$ - l'angolo tra le direzioni della corrente e dell'induzione magnetica. Allora perché sta succedendo questo?

Forza di Lorentz. Movimento di una particella carica in un campo magnetico.

Contenuto

1 Cos'è la forza di Lorentz - definizione, quando si verifica, ottenere la formula
2 Determinazione della direzione della forza di Lorentz usando la regola della mano sinistra
3 Movimento di una particella carica in un campo magnetico
4 Applicazione della forza di Lorentz in ingegneria

Cos'è la forza di Lorentz - definizione, quando nasce, derivazione della formula

Si sa che la corrente elettrica è il movimento ordinato di particelle cariche. Si sa anche che mentre si muove in un campo magnetico, ciascuna di queste particelle è soggetta a una forza. Perché si verifichi una forza, una particella deve essere in movimento.

La forza di Lorentz è la forza che agisce su una particella elettricamente carica mentre si muove in un campo magnetico. La sua direzione è ortogonale al piano in cui si trovano i vettori di velocità della particella e l'intensità del campo magnetico. La forza di Lorentz è la forza di Ampere. Conoscendola, si può ricavare la formula della forza di Lorentz.

Il tempo necessario a una particella per attraversare una sezione di un conduttore, $t = \frac {l}{v}$ dove $l$ - è la lunghezza del segmento, $v$ - velocità della particella. La carica totale trasportata durante questo tempo attraverso la sezione trasversale del conduttore, $Q = I\cdot t$ . Sostituendo qui il valore del tempo dall'equazione precedente, abbiamo

$Q = \frac {I\cdot l}{v}$ (2)

Allo stesso tempo $F_A = F_L\cdot N$ dove $N$ - è il numero di particelle nel conduttore considerato. Allo stesso tempo $N = \frac {Q}{q}$ dove $q$ - è la carica di una particella. Sostituendo nella formula $Q$ dalla (2), si può ottenere:

$N = \frac {I\cdot l}{v\cdot q}$

Così,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Usando la (1), l'espressione precedente può essere scritta come

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Dopo tagli e trasferimenti si ottiene la formula per il calcolo della forza di Lorentz

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Dato che la formula è scritta per un modulo di forza, dovrebbe essere scritta come segue:

$F_L = q||cdot v\cdot B\cdot sin\alpha$ (3)

Dal momento che $sin\alpha = sin(180^{{circ} - \alpha)$ , non ha importanza per il calcolo del modulo di Lorentz se la velocità è nella direzione della corrente o contro di essa, e possiamo dire che $\alpha$ - è l'angolo formato dai vettori di velocità della particella e l'induzione magnetica.

Scrivere la formula in forma vettoriale sarà così:

$\vec{F_L} = q\cdot [\vec{v}v volte \vec{B}]$

$[vvec{v} volte \vec{B}]$ - è il prodotto vettoriale, il cui risultato è un vettore con modulo uguale a $v\cdot B\cdot sin\alpha$ .

Dalla formula (3) possiamo concludere che la forza di Lorentz è massima nel caso di perpendicolarità delle direzioni della corrente elettrica e del campo magnetico, cioè a $\alpha = 90^{{circa}$ e scomparirà al loro parallelismo ( $\alpha = 0^{{circ.}$ ).

Va ricordato che per fornire una risposta quantitativa corretta - per esempio nella risoluzione di problemi - si dovrebbero usare le unità SI, in cui l'induzione magnetica si misura in tesla (1 Tesla = 1 kg-c⁻²-А⁻¹), forza in newton (1 N = 1 kg-m/s²), corrente in ampere, carica in coulons (1 Cl = 1 A-s), lunghezza in metri, velocità in m/s.

Determinazione della direzione della forza di Lorentz usando la regola della mano sinistra

Poiché nel mondo dei macro oggetti la forza di Lorentz si manifesta come una forza di Ampere, possiamo usare la regola della mano sinistra per trovare la sua direzione.

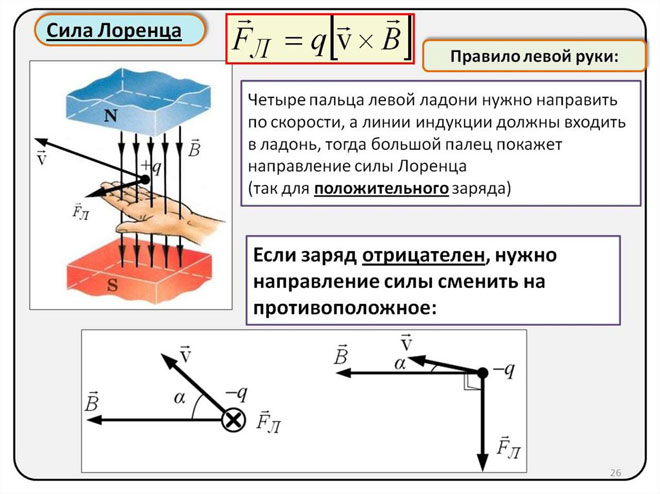
Determinazione della direzione della forza di Lorentz usando la regola della mano sinistra.

Con la mano sinistra posizionata perpendicolarmente e di fronte alle linee del campo magnetico, le quattro dita dovrebbero essere estese nella direzione della corrente, quindi la forza di Lorentz sarà diretta dove punta il pollice, che dovrebbe essere piegato.

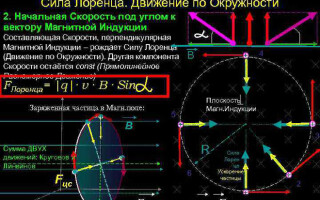
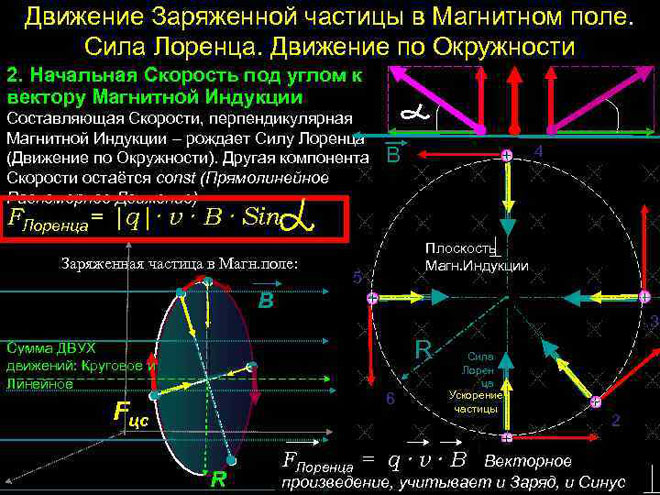
Movimento di una particella carica in un campo magnetico

Nel caso più semplice, cioè con l'ortogonalità dei vettori dell'induzione magnetica e della velocità della particella, la forza di Lorentz essendo perpendicolare al vettore velocità, può solo cambiare la sua direzione. La grandezza della velocità, quindi, l'energia rimarrà invariata. Quindi la forza di Lorentz agisce per analogia con la forza centripeta in meccanica e la particella si muove in un cerchio.

Secondo la seconda legge di Newton ( $F = m\cdot a$ ) si può determinare il raggio di rotazione di una particella:

$N = \frac {m\cdot v}{q\cdot B}$ .

Va notato che al variare della carica specifica della particella ( $\frac {q}{m}$ ) cambia anche il raggio.

Così il periodo di rotazione T = . $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Non dipende dalla velocità, quindi la posizione reciproca di particelle con velocità diverse sarà la stessa.

Il moto di una particella carica in un campo magnetico omogeneo.

Nel caso più complicato, quando l'angolo tra la velocità della particella e l'intensità del campo magnetico è arbitrario, essa si muoverà lungo una traiettoria elicoidale - progressivamente a spese della componente di velocità diretta parallela al campo, e circonferenzialmente all'influenza della sua componente perpendicolare.

Applicazioni della forza di Lorentz in ingegneria

Kinescope

Il cinescopio, che fino a poco tempo fa, quando è stato sostituito dall'LCD (schermo piatto), era in ogni televisore, non avrebbe potuto funzionare senza la forza di Lorentz. Per formare un'immagine televisiva sullo schermo, un flusso stretto di elettroni sono bobine deflettrici che generano un campo magnetico linearmente variabile. Le bobine di linea muovono il fascio di elettroni da sinistra a destra e indietro, mentre le bobine del telaio sono responsabili del movimento verticale, muovendo il fascio in esecuzione orizzontalmente dall'alto in basso. Lo stesso principio è usato in oscilloscopi - strumenti utilizzati per studiare le tensioni elettriche alternate.

Spettrografo di massa

Uno spettrografo di massa è uno strumento che utilizza la relazione tra il raggio di rotazione di una particella carica e la sua carica specifica. Il suo principio di funzionamento è il seguente:

Una fonte di particelle cariche, che guadagnano velocità per mezzo di un campo elettrico creato artificialmente, è posta in una camera a vuoto per eliminare l'influenza delle molecole d'aria. Le particelle volano fuori dalla sorgente e, seguendo un arco di cerchio, colpiscono una lastra fotografica, lasciando delle tracce su di essa. A seconda della carica specifica, cambia il raggio della traiettoria e quindi il punto di impatto. Questo raggio è facile da misurare e, conoscendolo, si può calcolare la massa della particella. Utilizzando uno spettrografo di massa, per esempio, è stata studiata la composizione del suolo lunare.

Ciclotrone

L'indipendenza del periodo e quindi della frequenza di rotazione di una particella carica dalla sua velocità in presenza di un campo magnetico è utilizzata in un apparecchio chiamato ciclotrone, progettato per accelerare particelle ad alta velocità. Il ciclotrone consiste in due semicilindri metallici cavi, i duanti (ognuno a forma di lettera latina D), posti con i loro lati dritti uno di fronte all'altro a breve distanza.

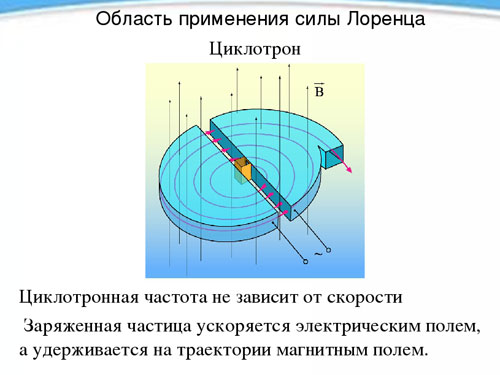
Ciclotrone - applicazione della forza di Lorentz.

I duanti sono posti in un campo magnetico omogeneo costante, e tra loro si crea un campo elettrico alternato, la cui frequenza è uguale alla frequenza di rotazione della particella, determinata dall'intensità del campo magnetico e dalla carica specifica. Essendo influenzata dal campo elettrico due volte durante il periodo di rotazione (quando passa da un duante all'altro), la particella viene accelerata ogni volta, aumentando così il raggio della traiettoria, e ad un certo momento, avendo guadagnato la velocità necessaria, vola fuori dal dispositivo attraverso il foro. In questo modo si può accelerare un protone a un'energia di 20 MeVmega electronvolt).

Magnetron

Un dispositivo chiamato magnetron, che è installato in ogni forno a microondeè un altro esempio di un apparecchio che funziona utilizzando la forza di Lorentz. Il magnetron crea un forte campo di microonde che riscalda il volume interno del forno in cui si trova il cibo. I magneti nel magnetron regolano il percorso degli elettroni all'interno del forno.

Il campo magnetico terrestre

In natura, la forza di Lorentz è molto importante per l'uomo. La sua presenza permette al campo magnetico terrestre di proteggere l'uomo dalle mortali radiazioni ionizzanti dello spazio. Il campo impedisce alle particelle cariche di bombardare la superficie del pianeta, costringendole a cambiare direzione.