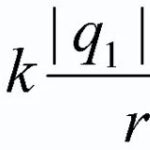A Lorentz-erő és a bal kéz szabálya. A töltött részecskék mozgása mágneses térben

Mágneses mezőbe helyezett vezető vezetőamelyen keresztül egy elektromos áram elektromos áramaz Amper-erő befolyásolja $F_A$ , és nagysága a következő képlettel számítható ki

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

ahol $I$ и $l$ - áramerősség és a vezeték hossza, $B$ - a mágneses mező indukciója, $\alpha$ - az áram és a mágneses indukció iránya közötti szög. Miért történik ez?

Lorentz-erő. Egy töltött részecske mozgása mágneses térben.

Tartalomjegyzék

1 Mi a Lorentz-erő - definíció, mikor fordul elő, a képlet megszerzése
2 A Lorentz-erő irányának meghatározása a balkezes szabály segítségével
3 Egy töltött részecske mozgása mágneses térben
4 A Lorentz-erő alkalmazása a mérnöki gyakorlatban

Mi a Lorentz-erő - definíció, mikor keletkezik, a képlet levezetése

Köztudott, hogy az elektromos áram a töltött részecskék rendezett mozgása. Az is ismert, hogy a mágneses térben való mozgás közben minden egyes ilyen részecskére erő hat. Ahhoz, hogy egy erő létrejöjjön, egy részecskének mozgásban kell lennie.

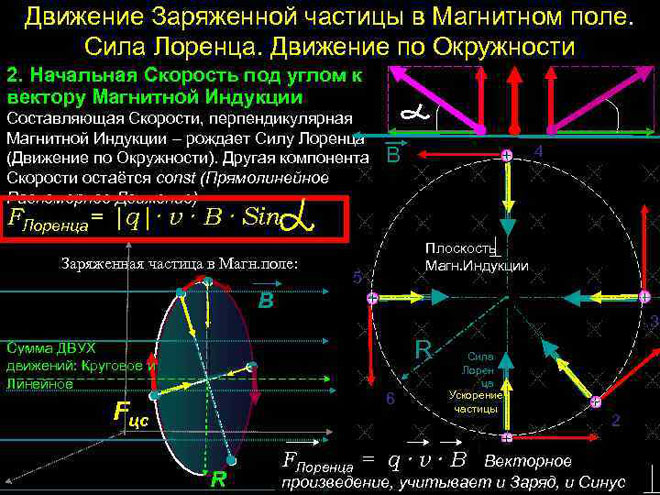
A Lorentz-erő az az erő, amely egy elektromosan töltött részecskére hat, amikor az mágneses térben mozog. Az iránya merőleges arra a síkra, amelyben a részecske sebességvektorai és a mágneses térerősség fekszenek. A Lorentz-erő az Amper-erő. Ennek ismeretében levezethető a Lorentz-erő képlete.

Az az idő, amely alatt egy részecske áthalad a vezető egy szakaszán, $t = \frac {l}{v}$ ahol $l$ - a szegmens hossza, $v$ - a részecske sebessége. Az ez idő alatt a vezető keresztmetszetén átvitt teljes töltés, $Q = I\cdot t$ . Az idő értékét az előző egyenletből ide behelyettesítve az alábbiakat kapjuk

$Q = \frac {I\cdot l}{v}$ (2)

Ugyanakkor $F_A = F_L\\cdot N$ ahol $N$ - a részecskék száma a vizsgált vezetőben. Ugyanakkor $N = \frac {Q}{q}$ ahol $q$ - egy részecske töltése. A képletbe behelyettesítve $Q$ a (2)-ből megkaphatjuk:

$N = \frac {I\cdot l}{v\cdot q}$

Így,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Az (1) segítségével az előző kifejezés a következőképpen írható fel

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Vágások és átvitelek után megkapjuk a Lorentz-erő kiszámításához szükséges képletet

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Tekintettel arra, hogy a képletet az erők modulusára írják, azt a következőképpen kell leírni:

Olvassa el továbbá: Hogyan kell átszámítani az ampereket wattra és vissza?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Mivel $sin\alpha = sin(180^{\circ} - \alpha)$ , a Lorentz-modul számítása szempontjából nem számít, hogy a sebesség az áramlás irányába vagy ellenkező irányba mutat, és azt mondhatjuk, hogy $\alpha$ - a részecske sebességvektora és a mágneses indukció által bezárt szög.

A képlet vektoros formában való leírása így néz ki:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\times \vec{B}]$ - az a vektorproduktum, amely egy olyan vektort eredményez, amelynek modulusa egyenlő $v\cdot B\cdot sin\alpha$ .

A (3) képletből megállapíthatjuk, hogy a Lorentz-erő maximális abban az esetben, ha az elektromos áram és a mágneses tér iránya merőleges egymásra, azaz a $\alpha = 90^{\circ}$ , és eltűnik a párhuzamosságuknál ( $\alpha = 0^{\\\circ}$ ).

Nem szabad elfelejteni, hogy a helyes mennyiségi válasz megadásához - például a feladatmegoldás során - SI-egységeket kell használni, amelyekben a mágneses indukciót teslában mérik (1 Tesla = 1 kg-c⁻²-А⁻¹), erő newtonban kifejezve (1 N = 1 kg-m/s²), áram amperben, töltés coulonban (1 Cl = 1 A-s), hossz méterben, sebesség m/s.

A Lorentz-erő irányának meghatározása a balkezes szabály segítségével

Mivel a makroobjektumok világában a Lorentz-erő Amper-erőként jelentkezik, a balkezes szabályt használhatjuk az irányának meghatározására.

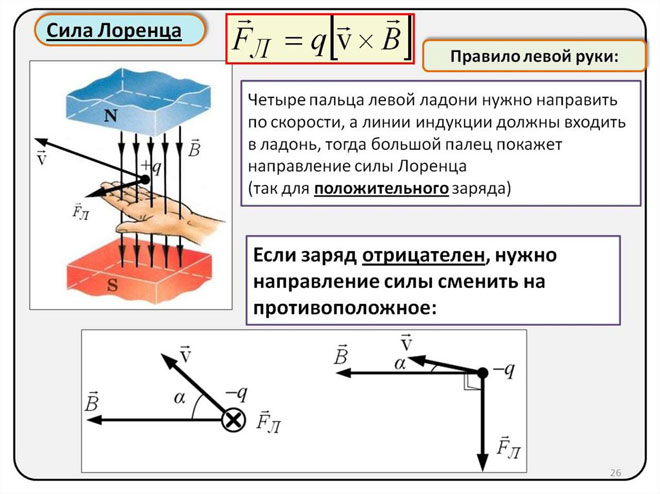
A Lorentz-erő irányának meghatározása a balkezes szabály segítségével.

A bal kézzel a mágneses mezővonalakra merőlegesen és azokkal szemben állva a négy ujjat az áram irányába kell kinyújtani, ekkor a Lorentz-erő arra irányul, amerre a hüvelykujj, amelynek hajlítva kell lennie, mutat.

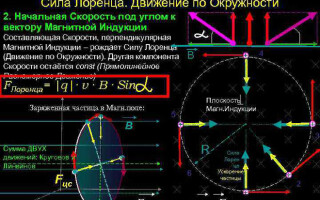
Egy töltött részecske mozgása mágneses térben

A legegyszerűbb esetben, azaz a mágneses indukció és a részecske sebességvektorának ortogonalitása esetén a Lorentz-erő, amely merőleges a sebességvektorra, csak az irányát változtathatja meg. A sebesség nagysága, tehát az energia változatlan marad. A Lorentz-erő tehát a mechanikában a centripetális erőhöz hasonlóan hat, és a részecske körpályán mozog.

Olvassa el továbbá: Hány watt van egy kilowattban?

Newton második törvénye szerint ( $F = m\cdot a$ ) meghatározható a részecske forgási sugara:

$N = \frac {m\cdot v}{q\cdot B}$ .

Meg kell jegyezni, hogy a részecske fajlagos töltésének változásával ( $\frac {q}{m}$ ) a sugár is változik.

Így a forgási periódus T = . $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Nem függ a sebességtől, így a különböző sebességű részecskék kölcsönös helyzete azonos lesz.

Egy töltött részecske mozgása homogén mágneses térben.

Abban a bonyolultabb esetben, amikor a részecske sebessége és a mágneses térerősség közötti szög tetszőleges, a részecske spirális pályán fog mozogni - fokozatosan a mezővel párhuzamos sebességkomponens rovására, és körkörösen a rá merőleges komponens hatására.

A Lorentz-erő mérnöki alkalmazásai

Kinescope

A kineszkóp, amely egészen a közelmúltig, amikor az LCD (lapos képernyő) felváltotta, minden televízióban megtalálható volt, nem működhetett volna a Lorentz-erő nélkül. A képernyőn megjelenő televíziós kép kialakításához egy keskeny elektronáramot terelő tekercsek terelnek, amelyek lineárisan változó mágneses mezőt hoznak létre. A vonaltekercsek mozgatják az elektronsugarat balról jobbra és vissza, a kerettekercsek pedig a függőleges mozgásért felelősek, vízszintesen mozgatva a futó sugarat felülről lefelé. Ugyanezt az elvet alkalmazzák a oszcilloszkópok - váltakozó elektromos feszültségek vizsgálatára használt műszerek.

Tömegspektrográf

A tömegspektrográf egy olyan műszer, amely a töltött részecske forgási sugara és fajlagos töltése közötti összefüggést használja. Működési elve a következő:

A mesterségesen létrehozott elektromos tér segítségével sebességet nyerő töltött részecskék forrását vákuumkamrába helyezik, hogy kiküszöböljék a levegőmolekulák hatását. A részecskék kirepülnek a forrásból, és egy kör alakú ívet követve egy fotólemezbe csapódnak, nyomot hagyva rajta. Az adott töltettől függően változik a röppálya sugara és így a becsapódási pont is. Ez a sugár könnyen mérhető, és ennek ismeretében kiszámítható a részecske tömege. Tömegspektrográf segítségével például a holdi talaj összetételét tanulmányozták.

Olvassa el továbbá: Melyek a villamos energiával kapcsolatos szakmák

Ciklotron

A töltött részecske periódusának és így forgási frekvenciájának a mágneses tér jelenlétében mért sebességétől való függetlenségét egy ciklotron nevű berendezésben használják, amelyet részecskék nagy sebességre történő felgyorsítására terveztek. A ciklotron két üreges fémből készült félhengerből, duantokból (mindegyik egy latin D betű alakú), egyenes oldalaikkal egymással szemben, kis távolságban elhelyezve.

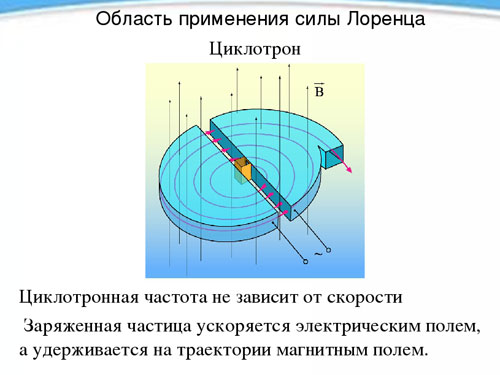
Ciklotron - a Lorentz-erő alkalmazása.

A duánsokat állandó homogén mágneses térbe helyezik, és váltakozó elektromos teret hoznak létre közöttük, amelynek frekvenciája megegyezik a részecske forgási frekvenciájával, amelyet a mágneses térerősség és a fajlagos töltés határoz meg. Mivel a forgási periódus alatt kétszer hat rá az elektromos mező (amikor az egyik duantból a másikba lép), a részecske minden alkalommal felgyorsul, így a pálya sugara megnő, és egy bizonyos pillanatban, miután elérte a szükséges sebességet, a lyukon keresztül kirepül a készülékből. Így egy proton 20 MeV energiára gyorsítható fel.mega elektronvolt).

Magnetron

Egy magnetron nevű eszköz, amelyet minden egyes mikrohullámú sütőegy másik példa egy olyan készülékre, amely a Lorentz-erő segítségével működik. A magnetron erős mikrohullámú mezőt hoz létre, amely felmelegíti a sütő belső térfogatát, amelybe az ételt helyezik. A magnetronban lévő mágnesek állítják be az elektronok útját a kemencében.

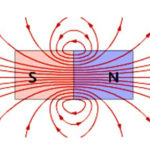
A Föld mágneses mezeje

A természetben a Lorentz-erő nagyon fontos az emberiség számára. Jelenléte lehetővé teszi, hogy a Föld mágneses mezeje megvédje az embereket az űr halálos ionizáló sugárzásától. A mező megakadályozza, hogy a töltött részecskék a bolygó felszínét bombázzák, és irányváltoztatásra kényszeríti őket.

Kapcsolódó cikkek: