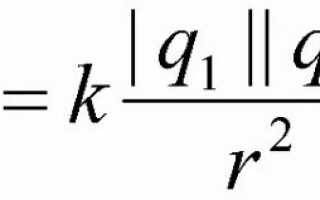Coulomb törvénye, definíció és képlet - elektromos ponttöltések és kölcsönhatásuk

A töltött testek között kölcsönhatási erő van, amely révén vonzzák vagy taszítják egymást. A Coulomb-törvény leírja ezt az erőt, és megmutatja, hogy a test méretétől és alakjától függően milyen mértékben hat. Ezzel a fizikai törvénnyel fogunk foglalkozni ebben a cikkben.

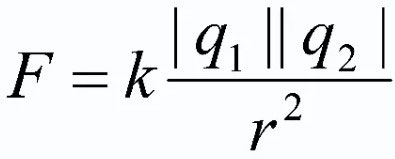
A Coulomb-törvény képlete.

Tartalomjegyzék

1 Helyhez kötött ponttöltések
2 Charles Coulomb torziós skálái
3 Az arányossági együttható k és az elektromos állandó
4 A Coulomb-erő iránya és vektoros megfogalmazása
5 Ahol a Coulomb-törvény a gyakorlatban érvényesül
6 Az erő iránya a Coulomb-törvényben
7 A felfedezés története

Helyhez kötött ponttöltések

A Coulomb-törvény olyan helyhez kötött testekre vonatkozik, amelyek mérete jóval kisebb, mint a többi tárgytól való távolságuk. Az ilyen testeken pontszerű elektromos töltés van. A fizikai problémák megoldásakor a kérdéses testek méreteit elhanyagolják, mert nincs nagy jelentőségük.

A gyakorlatban a nyugvóponti töltéseket a következőképpen ábrázolják:

Egy pont pozitív töltésű töltés q1. Pont pozitív töltésű töltés q2.

Ebben az esetben q₁ és q₂ - vannak pozitív elektromos töltések, és a Coulomb-erő hat rájuk (az ábrán nem látható). A pontobjektumok mérete nem számít.

Megjegyzés! A nyugvó töltések egy adott távolságban helyezkednek el egymástól, amit a feladatokban általában r betűvel jelölnek. A tanulmány további részében ezeket a díjakat vákuumban vizsgáljuk.

Charles Coulomb torziós skálái

Ez a Coulomb által 1777-ben kifejlesztett készülék segített levezetni a később róla elnevezett erő függését. A pontszerű töltések és a mágneses pólusok kölcsönhatásának tanulmányozására használják.

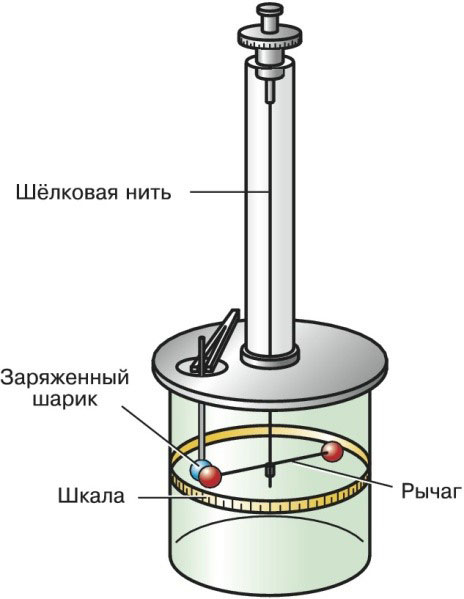
A torziós mérlegek egy függőleges síkban elhelyezett kis selyemszállal rendelkeznek, amelyen egy kiegyensúlyozott kar lóg. A kar végein pontszerű töltések vannak.

Külső erők hatására a kar vízszintes mozgásba kezd. A kar addig mozog a síkban, amíg a szál rugalmas ereje ki nem egyenlíti.

A mozgás során a kar a függőleges tengelytől egy bizonyos szögben elhajlik. Ezt d-nek vesszük, és elforgatási szögnek nevezzük. A paraméter értékének ismeretében meg lehet találni a fellépő erők nyomatékát.

Olvassa el továbbá: Mi az elektromos áram egyszerűbben fogalmazva

Charles Coulomb torziós skálái a következőképpen néznek ki:

Charles Coulomb torziós skálái.

Az arányossági együttható k és az elektromos állandó 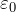$\varepsilon_0$

A Coulomb-törvény képletének paraméterei k - az arányossági együttható vagy $\varepsilon_0$ - elektromos állandó. Az elektromos állandó $\varepsilon_0$ számos szakkönyvben, tankönyvben, interneten szerepel, és nem kell kiszámítani! Az arányossági együttható a vákuumban a következők alapján $\varepsilon_0$ a jól ismert képlet szerint található:

$k = \frac {1}{4\cdot \pi\cdot \varepsilon_0}$

Itt $\varepsilon_0=8.85\cdot 10^{ -12} \frac {C^2}{H\cdot m^2}$ - elektromos állandó,

${\pi=3.14$ - a pi száma,

$k=9{cdot 10^{9} \frac {H\cdot m^2}{C^2}$ - az arányossági együttható vákuumban.

További információ! A fenti paraméterek ismerete nélkül nem lehetséges két pontszerű elektromos töltés közötti kölcsönhatási erő meghatározása.
A Coulomb-törvény megfogalmazása és formulája

A fentiek összefoglalásához meg kell adni az elektrosztatika fő törvényének formális megfogalmazását. Ez a következő formában történik:

Két nyugvó ponttöltés kölcsönhatási ereje vákuumban egyenesen arányos e töltések szorzatával és fordítottan arányos a köztük lévő távolság négyzetével. A töltések szorzatát pedig modulo kell venni!

$F=k\cdot \frac {|q_1|\cdot |q_2|}{r^2}$

Ebben a képletben q₁ és q₂- ponttöltések, a vizsgált testek; r² - az e testek közötti síkbeli távolság, négyzetben kifejezve; k az arányossági tényező ( $9\cdot 10^{9} \frac {H\cdot m^2}{C^2}$ vákuum esetén).

A Coulomb-erő iránya és a képlet vektoros formulája

A képlet teljes megértéséhez a Coulomb-törvény vizuálisan is ábrázolható:

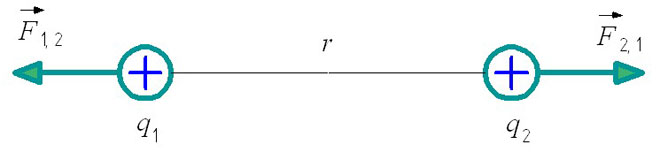
A Coulomb-erő iránya két azonos polaritású ponttöltés esetén.

F_1,2- az első töltés kölcsönhatási ereje a második töltéshez képest.

F_2,1- a második töltés kölcsönhatási ereje az elsőhöz képest.

Az elektrosztatikai feladatok megoldásakor fontos szabály az is, hogy a hasonló töltések taszítják, a hasonló töltések pedig vonzzák egymást. Ez határozza meg a kölcsönhatási erők helyzetét az ábrán.

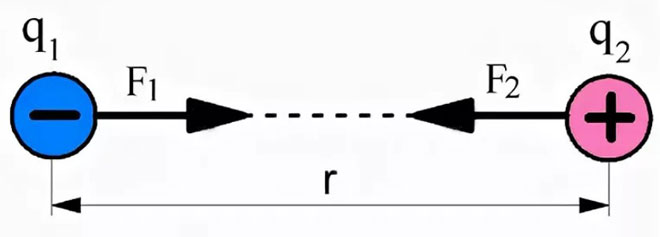
Ha ellentétes töltéseket veszünk figyelembe, akkor a kölcsönhatási erők egymás felé irányulnak, ami a vonzásukat jelenti.

A Coulomb-erő iránya két különböző polaritású ponttöltés esetén.

Az elektrosztatika alaptörvényének képlete vektoros formában a következőképpen ábrázolható

$\vec F_1_2=\frac {1}{4\cdot \pi\cdot \varepsilon_0}\cdot \frac {q_1\cdot q_2}{r_1_2^3}\cdot \vec r_1_2$

$\vec F_1_2$ - A q1 ponttöltésre ható erő a q2 töltésoldalon,

${\vec r_1_2}$ - a q2 töltést a q1 töltéssel összekötő sugárvektor,

Olvassa el továbbá: Hogyan készítsünk elektronikus áramkört otthon?

$r=||||\\vec r_1_2|$

Fontos! Ha a képletet vektoros formában írjuk fel, akkor két pontszerű elektromos töltés kölcsönhatását a tengelyre kell vetíteni, hogy a jeleket helyesen helyezzük el. Ez a művelet formaság, és gyakran mentálisan, jegyzetek nélkül történik.

Ahol a Coulomb-törvény a gyakorlatban érvényesül

Az elektrosztatika alaptörvénye Charles Coulomb legfontosabb felfedezése, amely számos területen talált alkalmazásra.

A híres fizikus munkásságát különböző eszközök, műszerek és készülékek feltalálása során használták fel. Például a villámhárító.

A villámhárítókat arra használják, hogy megvédjék a házakat és az épületeket a villámoktól a zivatarok idején. Ez növeli az elektromos berendezések védelmi fokát.

A villámhárítók a következő elven működnek: zivatarban a földön fokozatosan erős indukciós töltések keletkeznek, amelyek aztán felfelé szállnak, és a felhők vonzzák őket. Ez nagy elektromos mezőt hoz létre a talajon. A villámhárító közelében az elektromos mező erősebbé válik, így a készülék hegyéből koronaszerű elektromos töltés gyullad ki.

A talajon kialakult töltés ekkor a felhőn lévő töltés ellenkező előjellel vonzza a felhőt, ahogyan azt a Coulomb-törvény szerint tennie kell. A levegő ekkor ionizációs folyamaton megy keresztül, és az elektromos térerősség a villámhárító vége felé csökken. Így minimális a kockázata annak, hogy villámcsapás éri az épületet.

Kérjük, vegye figyelembe! Ha egy olyan épületbe csapnak be, amelyre villámhárítót szereltek, nem keletkezik tűz, hanem az összes energia a talajba távozik.

A Coulomb-törvény alapján kifejlesztettek egy "részecskegyorsító" nevű eszközt, amelyre ma nagy a kereslet.

Ez a készülék erős elektromos mezőt hoz létre, ami növeli a belépő részecskék energiáját.

Az erők iránya a Coulomb-törvényben

Mint fentebb említettük, két pontszerű elektromos töltés kölcsönhatásának iránya a polaritásuktól függ. Vagyis az azonos polaritású hasonló töltések taszítják egymást, az ellentétes polaritású töltések pedig vonzzák egymást.

Olvassa el továbbá: Hogyan készítsünk fémdetektort saját kezűleg, kezdő segítséggel

A Coulomb-erőket sugárvektornak is nevezhetjük, mert a közöttük húzott vonal mentén irányulnak.

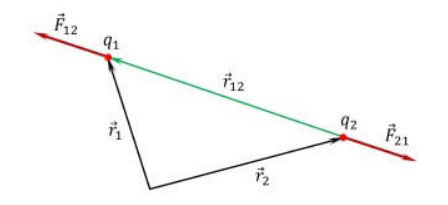
Egyes fizikai feladatokban olyan összetett alakú testek adottak, amelyek nem vehetők pontszerű elektromos töltésnek, azaz a méreteit elhanyagoljuk. Ilyen helyzetben a kérdéses testet több kis részre kell bontani, és minden egyes részt külön-külön kell kiszámítani a Coulomb-törvény alkalmazásával.

A felbontásukkal kapott erővektorokat az algebra és a geometria szabályai szerint összegezzük. Az eredmény a keletkező erő, amely a probléma megoldása. Ezt a megoldási módszert gyakran háromszögmódszernek nevezik.

A Coulomb-erő vektorok iránya.

A jog felfedezésének története

Két pontszerű töltés kölcsönhatását a fent tárgyalt törvény alapján először 1785-ben Charles Coulomb bizonyította be. A fizikusnak a megfogalmazott törvény igazságát torziós mérlegek segítségével sikerült bizonyítania, amelynek elvét a cikkben is bemutatta.

Coulomb azt is bebizonyította, hogy egy gömb alakú kondenzátor belsejében nincs elektromos töltés. Így jutott el ahhoz a megállapításhoz, hogy az elektrosztatikus erők nagysága megváltoztatható a kérdéses testek közötti távolság változtatásával.

Így Coulomb törvénye még mindig az elektrosztatika legfontosabb törvénye, amely alapján számos nagy felfedezés született. Ebben a cikkben a törvény hivatalos megfogalmazását mutattuk be, és részletesen ismertettük a törvény alkotóelemeit.

Kapcsolódó cikkek: