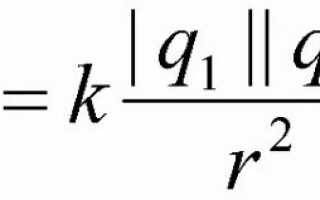आवेशित पिंडों के बीच एक अंतःक्रियात्मक बल होता है, जिसके माध्यम से वे एक दूसरे को आकर्षित या प्रतिकर्षित कर सकते हैं। कूलम्ब का नियम इस बल का वर्णन करता है और शरीर के आकार और आकार के आधार पर इसके प्रभाव की सीमा को दर्शाता है। इस लेख में इस भौतिक नियम पर चर्चा की जाएगी।
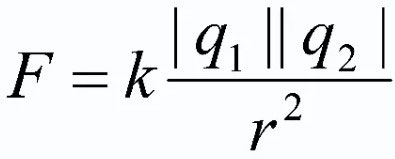
अंतर्वस्तु
स्थिर बिंदु शुल्क
कूलम्ब का नियम स्थिर पिंडों पर लागू होता है जिनका आकार अन्य वस्तुओं से उनकी दूरी से बहुत छोटा होता है। ऐसे पिंडों पर एक बिंदु विद्युत आवेश केंद्रित होता है। शारीरिक समस्याओं को हल करते समय, प्रश्न में निकायों के आकार की उपेक्षा की जाती है, क्योंकि वे ज्यादा मायने नहीं रखते।
व्यवहार में, विश्राम बिंदु प्रभारों को निम्नानुसार दर्शाया गया है:


इस मामले में क्यू1 और क्यू2 - हैं सकारात्मक विद्युत आवेश, और कूलम्ब बल उन पर कार्य करता है (चित्र में नहीं दिखाया गया है)। बिंदु वस्तुओं का आकार कोई फर्क नहीं पड़ता।
टिप्पणी! रेस्टिंग चार्ज एक दूसरे से एक निश्चित दूरी पर स्थित होते हैं, जिसे समस्याओं में आमतौर पर r अक्षर से दर्शाया जाता है। आगे कागज में हम इन आरोपों पर निर्वात में विचार करेंगे।
चार्ल्स कूलम्ब का मरोड़ तराजू
1777 में कूलम्ब द्वारा विकसित इस उपकरण ने बल की निर्भरता को प्राप्त करने में मदद की, जिसे बाद में उनके नाम पर रखा गया। इसका उपयोग बिंदु आवेशों के साथ-साथ चुंबकीय ध्रुवों की परस्पर क्रिया का अध्ययन करने के लिए किया जाता है।
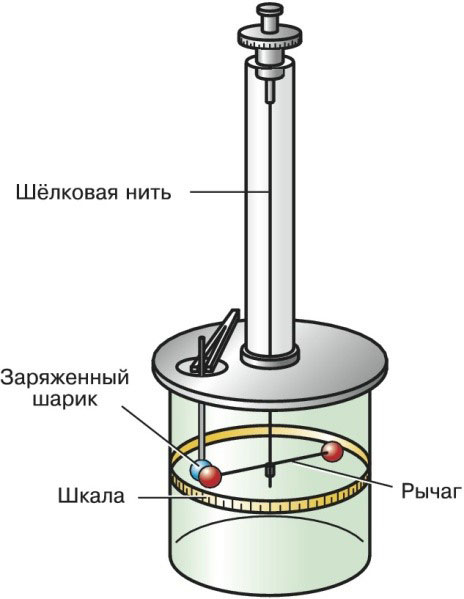
मरोड़ के तराजू में एक छोटा रेशमी धागा होता है, जो एक ऊर्ध्वाधर विमान में स्थित होता है, जिस पर एक संतुलित लीवर लटका होता है। लीवर के सिरों पर बिंदु आवेश होते हैं।
बाहरी बलों की कार्रवाई के तहत, लीवर क्षैतिज रूप से चलना शुरू कर देता है। लीवर विमान में तब तक गति करेगा जब तक कि यह धागे के लोचदार बल द्वारा संतुलित न हो जाए।
आंदोलन की प्रक्रिया में, लीवर एक निश्चित कोण से ऊर्ध्वाधर अक्ष से विचलित हो जाता है। इसे d के रूप में लिया जाता है और इसे घूर्णन कोण कहा जाता है। इस पैरामीटर के मूल्य को जानने के बाद, आप होने वाली ताकतों का टोक़ पा सकते हैं।
चार्ल्स कूलम्ब के मरोड़ वाले तराजू इस प्रकार दिखते हैं:
आनुपातिकता का गुणांक k और विद्युत स्थिरांक 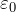
कूलम्ब के नियम सूत्र में पैरामीटर k हैं, आनुपातिकता का गुणांक या ![]() - विद्युत स्थिरांक। विद्युत स्थिरांक
- विद्युत स्थिरांक। विद्युत स्थिरांक ![]() कई संदर्भ पुस्तकों, पाठ्यपुस्तकों, इंटरनेट में प्रस्तुत किया गया है, और इसे गिनने की आवश्यकता नहीं है! निर्वात में आनुपातिकता का गुणांक पर आधारित है
कई संदर्भ पुस्तकों, पाठ्यपुस्तकों, इंटरनेट में प्रस्तुत किया गया है, और इसे गिनने की आवश्यकता नहीं है! निर्वात में आनुपातिकता का गुणांक पर आधारित है ![]() प्रसिद्ध सूत्र का उपयोग करके पाया जा सकता है:
प्रसिद्ध सूत्र का उपयोग करके पाया जा सकता है:
![]()
यहां ![]() - विद्युत स्थिरांक,
- विद्युत स्थिरांक,
![]() - नंबर पाई,
- नंबर पाई,
![]() - निर्वात में आनुपातिकता का गुणांक।
- निर्वात में आनुपातिकता का गुणांक।
अतिरिक्त जानकारी! उपरोक्त मापदंडों को जाने बिना, दो बिंदु विद्युत आवेशों के बीच परस्पर क्रिया बल का पता लगाना असंभव है।
कूलम्ब के नियम का सूत्रीकरण और सूत्र
उपरोक्त को संक्षेप में प्रस्तुत करने के लिए, इलेक्ट्रोस्टैटिक्स के मुख्य कानून का आधिकारिक सूत्रीकरण देना आवश्यक है। यह रूप लेता है:
निर्वात में दो विराम बिंदु आवेशों का परस्पर क्रिया बल इन आवेशों के गुणनफल के समानुपाती होता है और उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। और शुल्क के उत्पाद को मोडुलो लिया जाना चाहिए!
![]()
इस सूत्र में q1 और क्यू2 - बिंदु शुल्क हैं, माना निकाय; आर2 - एक वर्ग के रूप में ली गई इन निकायों के बीच एक विमान पर दूरी है; k आनुपातिकता का कारक है (![]() वैक्यूम के लिए)।
वैक्यूम के लिए)।
कूलम्ब बल की दिशा और सूत्र का सदिश रूप
सूत्र को पूरी तरह से समझने के लिए कूलम्ब के नियम को दृष्टिगत रूप से दर्शाया जा सकता है:
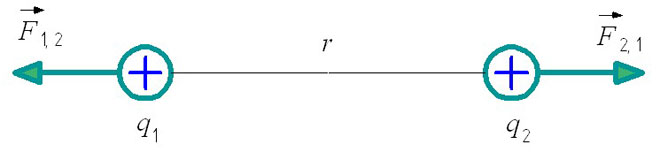
एफ1,2 - दूसरे के संबंध में पहले आवेश की परस्पर क्रिया बल है।
एफ2,1 - पहले के संबंध में दूसरे आवेश की परस्पर क्रिया बल है।
इसके अलावा, इलेक्ट्रोस्टैटिक्स की समस्याओं को हल करते समय, एक महत्वपूर्ण नियम को ध्यान में रखना आवश्यक है: समान-नामित विद्युत आवेश प्रतिकर्षित करते हैं और विपरीत-नाम वाले आवेश आकर्षित करते हैं। यह आकृति में अन्योन्यक्रिया बलों का स्थान निर्धारित करता है।
यदि विपरीत आरोपों पर विचार किया जाता है, तो उनकी अंतःक्रिया बलों को एक दूसरे की ओर निर्देशित किया जाएगा, जो उनके आकर्षण का प्रतिनिधित्व करते हैं।
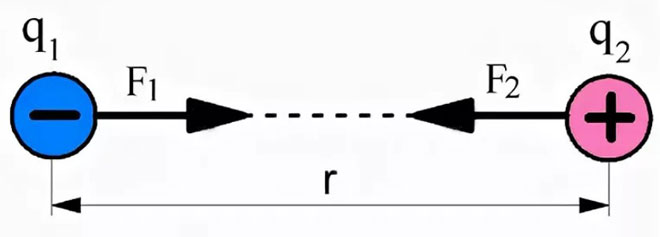
सदिश रूप में इलेक्ट्रोस्टैटिक्स के मूल कानून के सूत्र को निम्नानुसार दर्शाया जा सकता है:
![]()
![]() - बिंदु आवेश q1 पर कार्य करने वाला बल, आवेश q2 की तरफ,
- बिंदु आवेश q1 पर कार्य करने वाला बल, आवेश q2 की तरफ,
![]() - त्रिज्या-सदिश कनेक्टिंग चार्ज q2 चार्ज करने के लिए q1,
- त्रिज्या-सदिश कनेक्टिंग चार्ज q2 चार्ज करने के लिए q1,
![]()
महत्वपूर्ण! सूत्र को सदिश रूप में लिखने के बाद, संकेतों को सही ढंग से लगाने के लिए दो बिंदु विद्युत आवेशों की परस्पर क्रिया करने वाले बलों को अक्ष पर प्रक्षेपित करना होगा। यह क्रिया एक औपचारिकता है और अक्सर बिना किसी नोट के मानसिक रूप से की जाती है।
जहां व्यवहार में कूलम्ब का नियम लागू होता है
इलेक्ट्रोस्टैटिक्स का मूल नियम चार्ल्स कूलम्ब की सबसे महत्वपूर्ण खोज है, जिसने कई क्षेत्रों में अपना आवेदन पाया है।
प्रसिद्ध भौतिक विज्ञानी के काम का उपयोग विभिन्न उपकरणों, उपकरणों, उपकरणों के आविष्कार की प्रक्रिया में किया गया था। उदाहरण के लिए, बिजली की छड़।
बिजली की छड़ों के प्रयोग से घरों और इमारतों को गरज के साथ बिजली गिरने से बचाया जाता है। इस प्रकार, विद्युत उपकरणों की सुरक्षा की डिग्री बढ़ जाती है।
बिजली की छड़ें निम्नलिखित सिद्धांत पर काम करती हैं: एक गरज के दौरान मजबूत प्रेरण शुल्क धीरे-धीरे जमीन पर जमा हो जाते हैं, जो ऊपर उठते हैं और बादलों की ओर आकर्षित होते हैं। यह जमीन पर काफी विद्युत क्षेत्र बनाता है। बिजली की छड़ के पास, विद्युत क्षेत्र मजबूत हो जाता है, जिससे उपकरण की नोक से कोरोना विद्युत आवेश प्रज्वलित हो जाता है।
तब जमीन पर बना आवेश विपरीत चिन्ह वाले मेघ आवेश की ओर आकर्षित होने लगता है, जैसा कि चार्ल्स कूलम्ब के नियम के अनुसार होना चाहिए। फिर हवा को आयनित किया जाता है, और बिजली की छड़ के अंत के पास विद्युत क्षेत्र की ताकत कम हो जाती है। इस प्रकार, इमारत में बिजली गिरने का जोखिम न्यूनतम है।
कृपया ध्यान दें! यदि बिजली की छड़ से एक इमारत टकराती है, तो आग नहीं लगेगी, और सारी ऊर्जा जमीन में चली जाती है।
कूलम्ब के नियम के आधार पर, "कण त्वरक" नामक एक उपकरण विकसित किया गया था और आज इसकी बहुत मांग है।
यह उपकरण एक मजबूत विद्युत क्षेत्र बनाता है, जिससे इसमें प्रवेश करने वाले कणों की ऊर्जा बढ़ जाती है।
कूलम्ब के नियम में बलों की दिशा
जैसा कि ऊपर कहा गया है, दो बिंदु विद्युत आवेशों के परस्पर क्रिया बलों की दिशा उनकी ध्रुवता पर निर्भर करती है। अर्थात्, समान-पड़ोसी शुल्क प्रतिकर्षित करेंगे और विपरीत-पड़ोसी शुल्क आकर्षित होंगे।
कूलम्ब बलों को त्रिज्या-सदिश भी कहा जा सकता है, क्योंकि वे त्रिज्या-सदिश के समान हैं। उन्हें उनके बीच खींची गई रेखा के साथ निर्देशित किया जाता है।
कुछ भौतिक समस्याओं में जटिल आकार के पिंड होते हैं, जिन्हें एक बिंदु विद्युत आवेश के रूप में नहीं लिया जा सकता है, अर्थात इसके आकार की उपेक्षा करना। इस स्थिति में, विचाराधीन शरीर को कई छोटे भागों में विभाजित किया जाना चाहिए और कूलम्ब के नियम को लागू करते हुए प्रत्येक भाग की अलग-अलग गणना की जानी चाहिए।
विभाजन में प्राप्त बल सदिशों को बीजगणित और ज्यामिति के नियमों द्वारा अभिव्यक्त किया जाता है। परिणाम परिणामी बल है, जो समस्या का उत्तर होगा।समाधान की इस विधि को अक्सर त्रिभुज विधि के रूप में जाना जाता है।
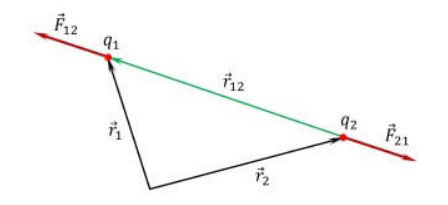
कानून की खोज का इतिहास
ऊपर चर्चा किए गए कानून द्वारा दो बिंदु आरोपों की बातचीत पहली बार 1785 में चार्ल्स कूलम्ब द्वारा सिद्ध की गई थी। भौतिक विज्ञानी मरोड़ तराजू का उपयोग करके तैयार कानून की सत्यता को साबित करने में कामयाब रहे, जिसके संचालन का सिद्धांत भी लेख में प्रस्तुत किया गया था।
कूलम्ब ने यह भी सिद्ध किया कि गोलाकार संधारित्र के अंदर कोई विद्युत आवेश नहीं होता है। इस प्रकार वह इस दावे पर पहुंचा कि विचाराधीन पिंडों के बीच की दूरी को बदलकर इलेक्ट्रोस्टैटिक बलों के परिमाण को बदला जा सकता है।
इस प्रकार, कूलम्ब का नियम अभी भी इलेक्ट्रोस्टैटिक्स का सबसे महत्वपूर्ण नियम है, जिसके आधार पर कई महान खोजें की गई हैं। इस लेख में कानून के आधिकारिक सूत्रीकरण को प्रस्तुत किया गया है, और इसके घटक भागों का विस्तार से वर्णन किया गया है।
संबंधित आलेख: