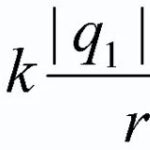लोरेंत्ज़ बल और बाएँ हाथ का नियम। चुंबकीय क्षेत्र में आवेशित कणों की गति

चुंबकीय क्षेत्र में रखा गया कंडक्टर...जिसके माध्यम से एक विद्युत प्रवाह ... एक विद्युत धाराएम्पीयर बल से प्रभावित होता है $एफ_ए$ , और इसके परिमाण की गणना निम्न सूत्र द्वारा की जा सकती है:

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

कहाँ पे $मैं$ और $मैं$ - कंडक्टर की वर्तमान ताकत और लंबाई, $बी$ - चुंबकीय क्षेत्र का प्रेरण, $\alpha$ - वर्तमान और चुंबकीय प्रेरण की दिशाओं के बीच का कोण। तो ऐसा क्यों हो रहा है?

लोरेंत्ज़ बल। चुंबकीय क्षेत्र में आवेशित कण की गति।

अंतर्वस्तु

1 लोरेंत्ज़ बल क्या है - परिभाषा, कब होती है, सूत्र प्राप्त करना
2 बाएं हाथ के नियम का उपयोग करके लोरेंत्ज़ बल की दिशा निर्धारित करना
3 चुंबकीय क्षेत्र में आवेशित कण की गति
4 इंजीनियरिंग में लोरेंत्ज़ बल के अनुप्रयोग

लोरेंत्ज़ बल क्या है - परिभाषा, कब उत्पन्न होती है, सूत्र प्राप्त करना

यह ज्ञात है कि विद्युत प्रवाह आवेशित कणों की क्रमबद्ध गति है। यह भी स्थापित किया गया है कि चुंबकीय क्षेत्र में चलते समय, इनमें से प्रत्येक कण एक बल के अधीन होता है। बल होने के लिए, कण गति में होना चाहिए।

लोरेंत्ज़ बल वह बल है जो एक विद्युत आवेशित कण पर कार्य करता है क्योंकि यह एक चुंबकीय क्षेत्र में चलता है। इसकी दिशा उस तल के ओर्थोगोनल है जिसमें कण के वेग वैक्टर और चुंबकीय क्षेत्र की ताकत निहित है।लोरेंत्ज़ बल एम्पीयर बल है। इसे जानने के बाद, हम लोरेंत्ज़ बल के लिए एक सूत्र प्राप्त कर सकते हैं।

एक कण को कंडक्टर के खिंचाव को पार करने के लिए आवश्यक समय, $टी = \ फ़्रेक {एल} {वी}$ कहाँ पे $मैं$ - खंड की लंबाई है, $वी$ - कण का वेग। इस दौरान कंडक्टर के क्रॉस सेक्शन के माध्यम से किया गया कुल चार्ज, $क्यू = मैं\cdot टी$ . यहाँ समय के मूल्य को पिछली समानता से प्रतिस्थापित करते हुए, हमारे पास है

$क्यू = \ फ़्रेक {मैं \ cdot l} {v}$ (2)

एक ही समय पर $F_A=F_L\cdot N$ कहाँ पे $एन$ - माना कंडक्टर में कणों की संख्या है। एक ही समय पर $एन = \ फ़्रेक {क्यू} {क्यू}$ कहाँ पे $क्यू$ - एक कण का आवेश है। सूत्र में प्रतिस्थापित करके का मान $क्यू$ (2) से, कोई प्राप्त कर सकता है:

$एन = \frac {मैं\cdot l}{v\cdot q}$

इस प्रकार,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

(1) का प्रयोग करते हुए, पिछले व्यंजक को इस प्रकार लिखा जा सकता है

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

लोरेंत्ज़ बल की गणना के लिए सूत्र में कटौती और स्थानान्तरण के बाद प्रकट होता है

$F_L = q\cdot v\cdot B\cdot sin\alpha$

यह देखते हुए कि बल के मापांक के लिए सूत्र लिखा गया है, इसे इस प्रकार लिखा जाना चाहिए:

यह भी पढ़ें: एम्पीयर को वाट और बैक में कैसे बदलें?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

तब से $sin\alpha = sin(180^{\circ} -\alpha)$ , लोरेंत्ज़ मापांक की गणना के लिए यह कोई मायने नहीं रखता है कि वेग वर्तमान बल की दिशा में निर्देशित है या इसके खिलाफ है, और हम कह सकते हैं कि $\alpha$ - कण के वेग वैक्टर और चुंबकीय प्रेरण द्वारा गठित कोण है।

सूत्र को सदिश रूप में लिखना इस प्रकार दिखाई देगा:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}$

$[\vec{v}\बार \vec{B}$ - वेक्टर उत्पाद है, जिसके परिणाम के बराबर मापांक वाला एक वेक्टर है $v\cdot B\cdot sin\alpha$ .

सूत्र (3) के आधार पर, हम यह निष्कर्ष निकाल सकते हैं कि विद्युत धारा और चुंबकीय क्षेत्र की दिशाओं के लंबवत होने की स्थिति में लोरेंत्ज़ बल अधिकतम होता है, अर्थात $\अल्फा = 90^{\सर्कल}$ और गायब हो जाते हैं जब वे समानांतर होते हैं ( $\अल्फा = 0^{\सर्कल}$ ).

याद रखें कि एक सही मात्रात्मक उत्तर प्रदान करने के लिए - उदाहरण के लिए, समस्याओं को हल करते समय - किसी को SI इकाइयों का उपयोग करना चाहिए, जिसमें चुंबकीय प्रेरण को टेस्ला में मापा जाता है (1 टेस्ला = 1 किग्रा-सी⁻²-А⁻¹), न्यूटन में बल (1 N = 1 kg-m/s²), एम्पीयर में करंट, कूलन में चार्ज (1 Cl = 1 A-s), मीटर में लंबाई, मीटर में गति।

बाएं हाथ के नियम का उपयोग करके लोरेंत्ज़ बल की दिशा निर्धारित करना

चूंकि मैक्रो ऑब्जेक्ट्स की दुनिया में लोरेंत्ज़ बल एक एम्पीयर बल के रूप में प्रकट होता है, हम इसकी दिशा निर्धारित करने के लिए बाएं हाथ के नियम का उपयोग कर सकते हैं।

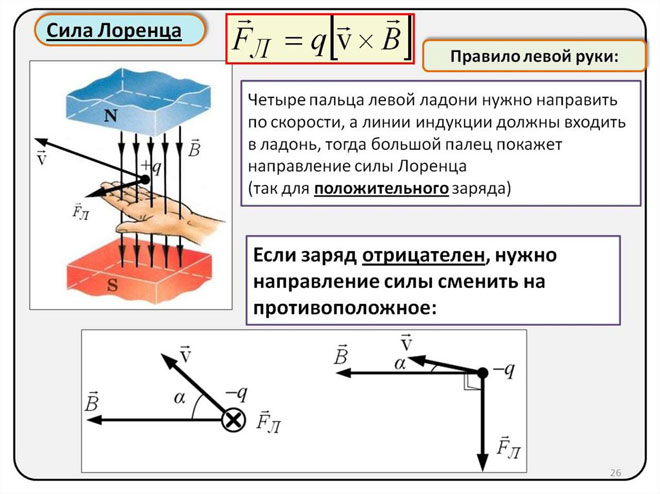
बाएं हाथ के नियम का उपयोग करके लोरेंत्ज़ बल की दिशा निर्धारित करना।

यदि आप अपना बायां हाथ रखते हैं ताकि आपकी खुली हथेली चुंबकीय क्षेत्र की रेखाओं के लंबवत हो और चार अंगुलियों को धारा की दिशा में बढ़ाया जाना चाहिए, तो लोरेंत्ज़ बल को निर्देशित किया जाएगा जहां आपका अंगूठा मुड़ा हुआ होना चाहिए , इशारा कर रहा है।

चुंबकीय क्षेत्र में आवेशित कण की गति

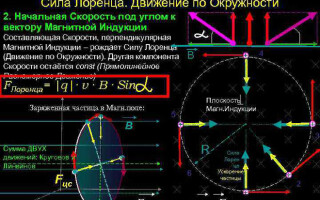
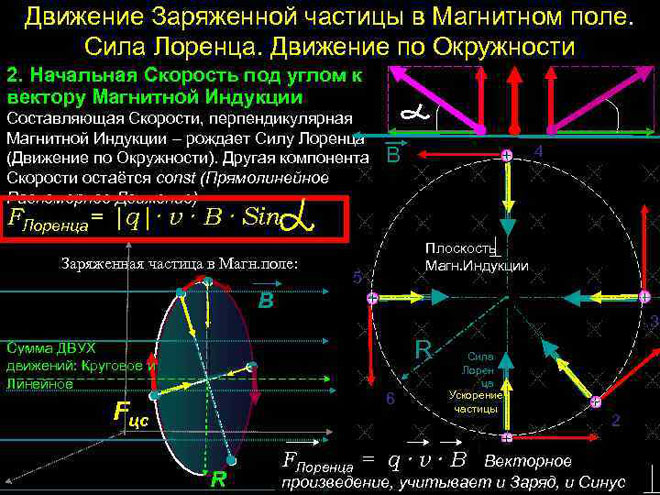
सबसे सरल मामले में, यानी चुंबकीय प्रेरण और कण के वेग के वैक्टर की ऑर्थोगोनैलिटी के साथ, लोरेंत्ज़ बल, वेग वेक्टर के लंबवत होने के कारण, केवल इसकी दिशा बदल सकता है। इसलिए, वेग का परिमाण और ऊर्जा अपरिवर्तित रहेगी। तो लोरेंत्ज़ बल यांत्रिकी में अभिकेन्द्र बल के साथ सादृश्य द्वारा कार्य करता है, और कण एक वृत्त में गति करता है।

यह भी पढ़ें: एक किलोवाट में कितने वाट होते हैं?

न्यूटन के द्वितीय नियम के अनुसार ( $एफ = एम\cdot a$ ) हम कण के घूर्णन की त्रिज्या निर्धारित कर सकते हैं:

$एन = \frac {एम\cdot v}{q\cdot बी}$ .

यह ध्यान दिया जाना चाहिए कि जैसे-जैसे कण का विशिष्ट आवेश बदलता है ( $\ फ़्रैक {क्यू} {एम}$ ), त्रिज्या भी बदल जाती है।

इस मामले में, रोटेशन की अवधि टी = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . यह वेग पर निर्भर नहीं करता है, इसलिए विभिन्न वेगों वाले कणों की पारस्परिक स्थिति समान होगी।

एक समांगी चुंबकीय क्षेत्र में आवेशित कण की गति।

अधिक जटिल मामले में, जब कण के वेग और चुंबकीय क्षेत्र की ताकत के बीच का कोण मनमाना होता है, तो यह एक पेचदार प्रक्षेपवक्र के साथ आगे बढ़ेगा - उत्तरोत्तर क्षेत्र के समानांतर निर्देशित वेग घटक की कीमत पर, और इसके प्रभाव में परिधि के साथ लंबवत घटक।

इंजीनियरिंग में लोरेंत्ज़ बल का अनुप्रयोग

कीनेस्कौप

किनेस्कोप, जो हाल तक, जब इसे एलसीडी (फ्लैट स्क्रीन) से बदल दिया गया था, हर टीवी सेट में था, लोरेंत्ज़ बल के बिना काम नहीं कर सकता था। इलेक्ट्रॉनों के एक संकीर्ण प्रवाह से स्क्रीन पर एक टेलीविजन छवि बनाने के लिए, विक्षेपण कॉइल का उपयोग एक रैखिक रूप से भिन्न चुंबकीय क्षेत्र बनाने के लिए किया जाता है।लाइन कॉइल इलेक्ट्रॉन बीम को बाएं से दाएं और पीछे ले जाते हैं, फ्रेम कॉइल ऊर्ध्वाधर आंदोलन के लिए जिम्मेदार होते हैं, जो बीम को ऊपर से नीचे की ओर क्षैतिज रूप से चलते हैं। में एक ही सिद्धांत का प्रयोग किया जाता है oscilloscopes - वैकल्पिक विद्युत वोल्टेज का अध्ययन करने के लिए।

मास स्पेक्ट्रोग्राफ

मास स्पेक्ट्रोग्राफ एक ऐसा उपकरण है जो किसी आवेशित कण के घूर्णन त्रिज्या की उसके विशिष्ट आवेश पर निर्भरता का उपयोग करता है। इसके संचालन का सिद्धांत इस प्रकार है:

आवेशित कणों का एक स्रोत, जो कृत्रिम रूप से निर्मित विद्युत क्षेत्र के माध्यम से गति प्राप्त करता है, वायु के अणुओं के प्रभाव को समाप्त करने के लिए निर्वात कक्ष में रखा जाता है। कण स्रोत से बाहर उड़ते हैं और, एक वृत्त के चाप से गुजरते हुए, एक फोटोग्राफिक प्लेट से टकराते हैं, उस पर निशान छोड़ते हैं। विशिष्ट चार्ज के आधार पर, प्रक्षेपवक्र त्रिज्या और इसलिए, प्रभाव का बिंदु बदल जाता है। इस त्रिज्या को मापना आसान है, और इसे जानकर आप कण के द्रव्यमान की गणना कर सकते हैं। मास स्पेक्ट्रोग्राफ का उपयोग करना, उदाहरण के लिए, चंद्र मिट्टी की संरचना का अध्ययन किया गया था।

यह भी पढ़ें: बिजली से संबंधित कुछ पेशे क्या हैं

साइक्लोट्रॉन

अवधि की स्वतंत्रता, और इसलिए एक चुंबकीय क्षेत्र की उपस्थिति में अपनी गति से एक आवेशित कण की रोटेशन आवृत्ति का उपयोग साइक्लोट्रॉन नामक एक उपकरण में किया जाता है, जिसे कणों को उच्च गति में गति देने के लिए डिज़ाइन किया गया है। साइक्लोट्रॉन दो खोखले धातु के अर्ध-सिलेंडर हैं, डुएंट्स (प्रत्येक एक लैटिन अक्षर D के आकार का है), उनके सीधे पक्षों के साथ थोड़ी दूरी पर एक दूसरे का सामना कर रखा है।

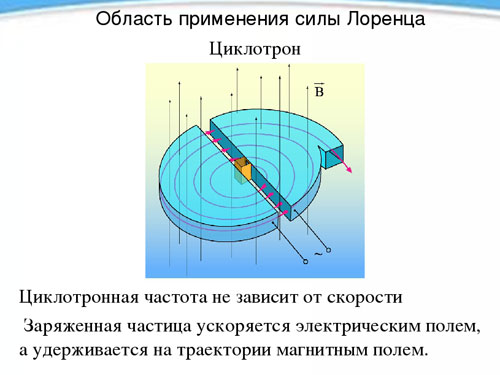
साइक्लोट्रॉन - लोरेंत्ज़ बल का अनुप्रयोग।

ड्यूएंट्स को एक निरंतर सजातीय चुंबकीय क्षेत्र में रखा जाता है, और उनके बीच एक वैकल्पिक विद्युत क्षेत्र बनाया जाता है, जिसकी आवृत्ति चुंबकीय क्षेत्र की ताकत और विशिष्ट चार्ज द्वारा निर्धारित कण रोटेशन की आवृत्ति के बराबर होती है।घूर्णन अवधि के दौरान दो बार विद्युत क्षेत्र के संपर्क में आने के कारण (एक डुअंट से दूसरे में संक्रमण के दौरान), कण हर बार तेज होता है, प्रक्षेपवक्र त्रिज्या को बढ़ाता है, और एक निश्चित क्षण में, आवश्यक वेग प्राप्त करने के बाद, यह बाहर उड़ जाता है छेद के माध्यम से डिवाइस। इस तरह कोई एक प्रोटॉन को 20 MeV . की ऊर्जा तक गति प्रदान कर सकता हैमेगा इलेक्ट्रॉनवोल्ट).

मैग्नेट्रान

मैग्नेट्रोन नामक एक उपकरण, जो प्रत्येक में स्थापित होता है माइक्रोवेव ओवनलोरेंत्ज़ बल का उपयोग करने वाले उपकरणों का एक अन्य प्रतिनिधि है। मैग्नेट्रोन का उपयोग एक शक्तिशाली माइक्रोवेव क्षेत्र बनाने के लिए किया जाता है जो ओवन की आंतरिक मात्रा को गर्म करता है जहां भोजन रखा जाता है। इसमें शामिल चुम्बक डिवाइस के अंदर इलेक्ट्रॉनों के प्रक्षेपवक्र को सही करते हैं।

पृथ्वी का चुंबकीय क्षेत्र

और प्रकृति में, लोरेंत्ज़ बल मानव जाति के लिए एक अत्यंत महत्वपूर्ण भूमिका निभाता है। इसकी उपस्थिति पृथ्वी के चुंबकीय क्षेत्र को अंतरिक्ष के घातक आयनकारी विकिरण से मनुष्यों की रक्षा करने की अनुमति देती है। क्षेत्र आवेशित कणों को ग्रह की सतह पर बमबारी करने से रोकता है, जिससे उन्हें दिशा बदलने के लिए मजबूर होना पड़ता है।