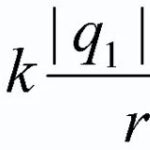La force de Lorentz et la règle de la main gauche. Mouvement des particules chargées dans un champ magnétique

Un conducteur placé dans un champ magnétique conducteurà travers lequel un courant électrique un courant électriqueest affecté par la force de l'Ampère $F_A$ et sa magnitude peut être calculée par la formule suivante

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

où $I$ и $l$ - l'ampérage et la longueur du conducteur, $B$ - l'induction du champ magnétique, $\alpha$ - l'angle entre les directions du courant et de l'induction magnétique. Alors pourquoi cela se produit-il ?

La force de Lorentz. Mouvement d'une particule chargée dans un champ magnétique.

Contenu

1 Qu'est-ce que la force de Lorentz - définition, quand elle se manifeste, obtention de la formule
2 Détermination de la direction de la force de Lorentz à l'aide de la règle de la main gauche
3 Mouvement d'une particule chargée dans un champ magnétique
4 Application de la force de Lorentz en ingénierie

Qu'est-ce que la force de Lorentz - définition, quand elle se manifeste, dérivation de la formule

On sait que le courant électrique est le mouvement ordonné de particules chargées. On sait également qu'en se déplaçant dans un champ magnétique, chacune de ces particules est soumise à une force. Pour qu'une force se produise, une particule doit être en mouvement.

La force de Lorentz est la force qui agit sur une particule chargée électriquement lorsqu'elle se déplace dans un champ magnétique. Sa direction est orthogonale au plan dans lequel se trouvent les vecteurs vitesse de la particule et l'intensité du champ magnétique. La force de Lorentz est la force de l'Ampère. En la connaissant, on peut déduire la formule de la force de Lorentz.

Le temps nécessaire à une particule pour traverser une section d'un conducteur, $t = \frac {l}{v}$ où $l$ - est la longueur du segment, $v$ - la vitesse de la particule. La charge totale transportée pendant ce temps à travers la section transversale du conducteur, $Q = I\cdot t$ . En substituant ici la valeur du temps de l'équation précédente, nous avons

$Q = \frac {I\cdot l}{v}$ (2)

Dans le même temps $F_A = F_L\\cdot N$ où $N$ - est le nombre de particules dans le conducteur considéré. Dans le même temps $N = \frac {Q}{q}$ où $q$ - est la charge d'une particule. En substituant dans la formule $Q$ de (2), on peut obtenir :

$N = \frac {I\cdot l}{v\cdot q}$

Ainsi,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

En utilisant (1), l'expression précédente peut être écrite comme suit

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Après des coupes et des transferts, nous obtenons la formule de calcul de la force de Lorentz

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Étant donné que la formule est écrite pour un module de force, elle devrait être écrite comme suit :

$F_L = |q||\cdot v\cdot B\cdot sin\alpha$ (3)

Depuis $sin\alpha = sin(180^{\circ} - \alpha)$ , il importe peu, pour le calcul du module de Lorentz, que la vitesse soit dans le sens du courant ou à contre-courant, et on peut dire que $\alpha$ - est l'angle formé par les vecteurs de vitesse de la particule et l'induction magnétique.

L'écriture de la formule sous forme vectorielle ressemblera à ceci :

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\N-times \vec{B}]$ - est le produit vectoriel résultant en un vecteur de module égal à $v\cdot B\cdot sin\alpha$ .

D'après la formule (3), on peut conclure que la force de Lorentz est maximale dans le cas de la perpendicularité des directions du courant électrique et du champ magnétique, c'est à dire à $\alpha = 90^{\circ}$ et disparaîtront à leur parallélisme ( $\alpha = 0^{\circ}$ ).

Il convient de rappeler que pour fournir une réponse quantitative correcte - par exemple dans la résolution de problèmes - il faut utiliser les unités SI, dans lesquelles l'induction magnétique est mesurée en teslas (1 Tesla = 1 kg-c⁻²-А⁻¹), force en newton (1 N = 1 kg-m/s²), courant en ampères, charge en coulons (1 Cl = 1 A-s), longueur en mètres, vitesse en m/s.

Détermination de la direction de la force de Lorentz à l'aide de la règle de la main gauche

Puisque dans le monde des macro-objets, la force de Lorentz se manifeste comme une force d'Ampère, nous pouvons utiliser la règle de la main gauche pour trouver sa direction.

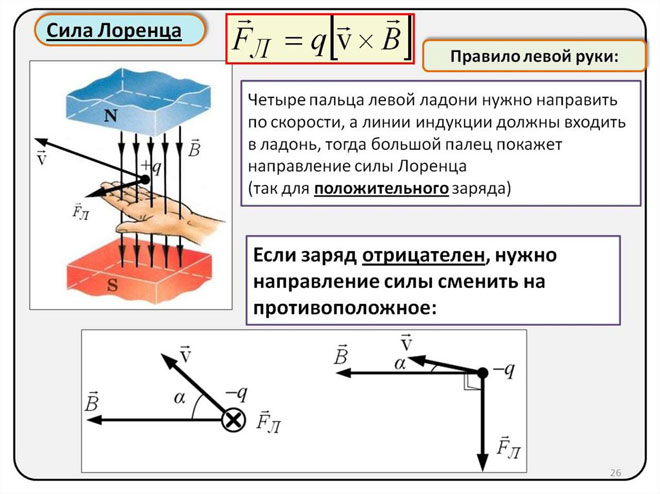
Déterminer la direction de la force de Lorentz en utilisant la règle de la main gauche.

Avec la main gauche placée perpendiculairement et face aux lignes de champ magnétique, les quatre doigts doivent être étendus dans la direction du courant, puis la force de Lorentz sera dirigée vers l'endroit où pointe le pouce, qui doit être plié.

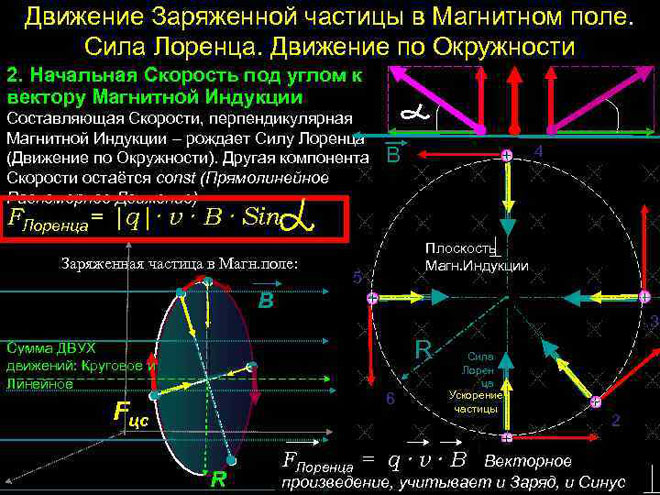
Mouvement d'une particule chargée dans un champ magnétique

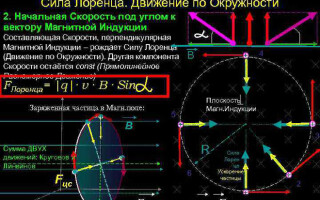
Dans le cas le plus simple, c'est-à-dire avec l'orthogonalité des vecteurs de l'induction magnétique et de la vitesse de la particule, la force de Lorentz étant perpendiculaire au vecteur vitesse, ne peut que changer sa direction. La magnitude de la vitesse, donc l'énergie, restera inchangée. La force de Lorentz agit donc par analogie avec la force centripète en mécanique et la particule se déplace dans un cercle.

Selon la deuxième loi de Newton ( $F = m\cdot a$ ) on peut déterminer le rayon de rotation d'une particule :

$N = \frac {m\cdot v}{q\cdot B}$ .

Il convient de noter que lorsque la charge spécifique de la particule change ( $\frac {q}{m}$ ), le rayon change également.

Ainsi, la période de rotation T = . $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Elle ne dépend pas de la vitesse, donc la position mutuelle de particules ayant des vitesses différentes sera la même.

Le mouvement d'une particule chargée dans un champ magnétique homogène.

Dans le cas plus compliqué où l'angle entre la vitesse de la particule et l'intensité du champ magnétique est arbitraire, elle se déplacera le long d'une trajectoire hélicoïdale - progressivement aux dépens de la composante de vitesse dirigée parallèlement au champ, et circonférentiellement à l'effet de sa composante perpendiculaire.

Applications de la force de Lorentz en ingénierie

Kinescope

Le kinéscope, qui jusqu'à récemment, lorsqu'il a été remplacé par le LCD (écran plat), se trouvait dans tous les téléviseurs, n'aurait pas pu fonctionner sans la force de Lorentz. Pour former une image de télévision sur l'écran, un flux étroit d'électrons passe par des bobines déflectrices qui génèrent un champ magnétique à variation linéaire. Les bobines de ligne déplacent le faisceau d'électrons de gauche à droite et inversement, les bobines de cadre sont responsables du mouvement vertical, déplaçant le faisceau mobile horizontalement de haut en bas. Le même principe est utilisé dans oscilloscopes - instruments utilisés pour étudier les tensions électriques alternatives.

Spectrographe de masse

Un spectrographe de masse est un instrument qui utilise la relation entre le rayon de rotation d'une particule chargée et sa charge spécifique. Son principe de fonctionnement est le suivant :

Une source de particules chargées, qui prennent de la vitesse grâce à un champ électrique créé artificiellement, est placée dans une chambre à vide pour éliminer l'influence des molécules d'air. Les particules s'envolent de la source et, suivant un arc de cercle, frappent une plaque photographique, y laissant des traces. En fonction de la charge spécifique, le rayon de la trajectoire et donc le point d'impact changent. Ce rayon est facile à mesurer et, en le connaissant, on peut calculer la masse de la particule. À l'aide d'un spectrographe de masse, par exemple, la composition du sol lunaire a été étudiée.

Cyclotron

L'indépendance de la période et donc de la vitesse d'une particule chargée par rapport à sa vitesse en présence d'un champ magnétique est utilisée dans un appareil appelé cyclotron, conçu pour accélérer les particules à des vitesses élevées. Le cyclotron est constitué de deux demi-cylindres métalliques creux, les duants (chacun ayant la forme d'une lettre latine D), placés avec leurs côtés droits se faisant face à une courte distance.

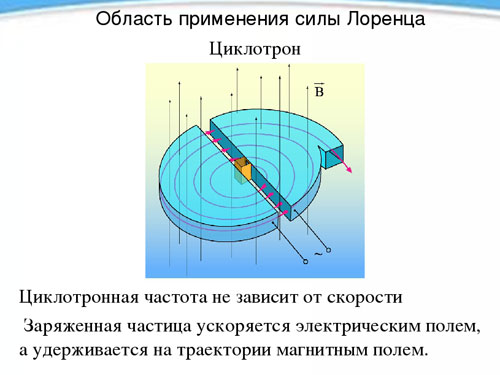
Cyclotron - application de la force de Lorentz.

Les duants sont placés dans un champ magnétique homogène constant, et un champ électrique alternatif est créé entre eux, dont la fréquence est égale à la fréquence de rotation de la particule, déterminée par l'intensité du champ magnétique et la charge spécifique. En étant influencée par le champ électrique deux fois pendant la période de rotation (lors du passage d'un canal à l'autre), la particule est accélérée à chaque fois, augmentant ainsi le rayon de la trajectoire, et à un moment donné, ayant acquis la vitesse nécessaire, elle s'envole hors du dispositif par le trou. De cette façon, on peut accélérer un proton à une énergie de 20 MeV.méga électronvolt).

Magnétron

Un dispositif appelé magnétron, qui est installé dans chaque four à micro-ondesest un autre exemple d'appareil qui fonctionne en utilisant la force de Lorentz. Le magnétron crée un puissant champ de micro-ondes qui réchauffe le volume interne du four dans lequel les aliments sont placés. Les aimants du magnétron ajustent la trajectoire des électrons à l'intérieur du four.

Le champ magnétique de la Terre

Dans la nature, la force de Lorentz est très importante pour l'homme. Sa présence permet au champ magnétique de la Terre de protéger les humains contre les rayonnements ionisants mortels de l'espace. Le champ empêche les particules chargées de bombarder la surface de la planète, les obligeant à changer de direction.