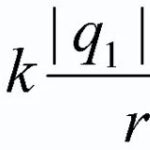Lorentzin voima ja vasemman käden sääntö. Varattujen hiukkasten liike magneettikentässä

Magneettikenttään sijoitettu johdin johtojonka läpi kulkee sähkövirta sähkövirtavaikuttaa ampeerivoima $F_A$ ja sen suuruus voidaan laskea seuraavalla kaavalla

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

jossa $I$ и $l$ - ampeeriluku ja johtimen pituus, $B$ - magneettikentän induktio, $\alpha$ - virran ja magneettisen induktion suuntien välinen kulma. Miksi näin tapahtuu?

Lorentzin voima. Varatun hiukkasen liike magneettikentässä.

Sisältö

1 Mikä on Lorentzin voima - määritelmä, milloin se esiintyy, kaavan saaminen
2 Lorentz-voiman suunnan määrittäminen vasemman käden säännön avulla
3 Varatun hiukkasen liike magneettikentässä
4 Lorentzin voiman soveltaminen tekniikassa

Mikä on Lorentz-voima - määritelmä, milloin se syntyy, kaavan johtaminen

Tiedetään, että sähkövirta on varattujen hiukkasten järjestäytynyttä liikettä. Tiedetään myös, että magneettikentässä liikkuessaan kuhunkin hiukkaseen kohdistuu voima. Jotta voima voisi vaikuttaa, hiukkasen on oltava liikkeessä.

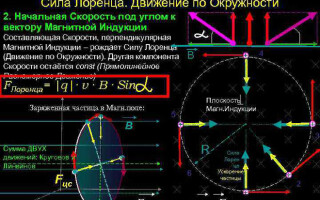
Lorentzin voima on voima, joka vaikuttaa sähköisesti varattuun hiukkaseen sen liikkuessa magneettikentässä. Sen suunta on kohtisuorassa siihen tasoon nähden, jossa hiukkasen nopeusvektorit ja magneettikentän voimakkuus sijaitsevat. Lorentzin voima on ampeerin voima. Kun se tunnetaan, Lorentzin voiman kaava voidaan johtaa.

Aika, jonka hiukkanen tarvitsee kulkeakseen johtimen osan läpi, $t = \frac {l}{v}$ jossa $l$ - on segmentin pituus, $v$ - hiukkasen nopeus. Tänä aikana johtimen poikkileikkauksen läpi kulkeva kokonaisvaraus, $Q = I\cdot t$ . Kun tähän korvataan edellisen yhtälön aika-arvo, saadaan

$Q = \frac {I\cdot l}{v}$ (2)

Samaan aikaan $F_A = F_L\\\cdot N$ jossa $N$ - on hiukkasten lukumäärä tarkastellussa johtimessa. Samaan aikaan $N = \frac {Q}{q}$ jossa $q$ - on yhden hiukkasen varaus. Korvaamalla kaavaan $Q$ (2), saadaan:

$N = \frac {I\cdot l}{v\cdot q}$

Niinpä,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Käyttämällä kohtaa (1) edellinen lauseke voidaan kirjoittaa seuraavasti

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Leikkausten ja siirtojen jälkeen saadaan Lorentz-voiman laskentakaava.

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Koska kaava on kirjoitettu voimamoduulille, se olisi kirjoitettava seuraavasti:

Lue myös: Kuinka muuntaa ampeerit wateiksi ja takaisin?

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Koska $sin\alpha = sin(180^{\circ} - \alpha)$ , Lorentz-moduulin laskemisen kannalta ei ole merkitystä sillä, onko nopeus virran suuntainen vai sitä vastaan, ja voimme sanoa, että $\alpha$ - on hiukkasen nopeusvektoreiden ja magneettisen induktion muodostama kulma.

Kaavan kirjoittaminen vektorimuodossa näyttää tältä:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\times \vec{B}]$ - on vektoritulo, jonka tuloksena saadaan vektori, jonka moduuli on yhtä suuri kuin $v\cdot B\cdot sin\alpha$ .

Kaavasta (3) voidaan päätellä, että Lorentz-voima on suurimmillaan, kun sähkövirran ja magneettikentän suunnat ovat kohtisuorassa toisiinsa nähden, eli kohdassa $\alpha = 90^{\circ}$ ja katoaa niiden rinnakkaisuudesta ( $\alpha = 0^{\\\circ}$ ).

On muistettava, että oikean kvantitatiivisen vastauksen antamiseksi - esimerkiksi ongelmanratkaisussa - on käytettävä SI-yksiköitä, joissa magneettista induktiota mitataan tesla-yksiköissä (1 Tesla = 1 kg-c).⁻²-А⁻¹), voima newtoneina (1 N = 1 kg-m/s)²), virta ampeereina, varaus couloneina (1 Cl = 1 A-s), pituus metreinä, nopeus m/s.

Lorentz-voiman suunnan määrittäminen vasemman käden säännön avulla

Koska makrokappaleiden maailmassa Lorentzin voima ilmenee ampeerivoimana, voimme käyttää vasemman käden sääntöä sen suunnan löytämiseksi.

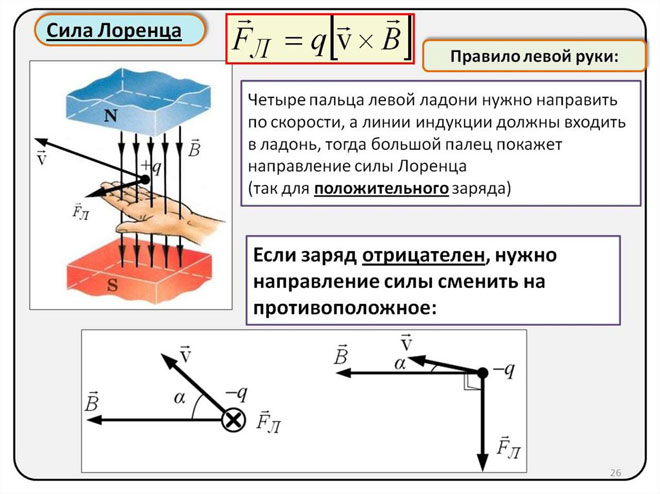
Lorentz-voiman suunnan määrittäminen vasemman käden säännön avulla.

Kun vasen käsi on kohtisuorassa magneettikentän linjoihin nähden, neljä sormea on ojennettava virran suuntaan, jolloin Lorentz-voima kohdistuu sinne, minne peukalo, jonka pitäisi olla taivutettuna, osoittaa.

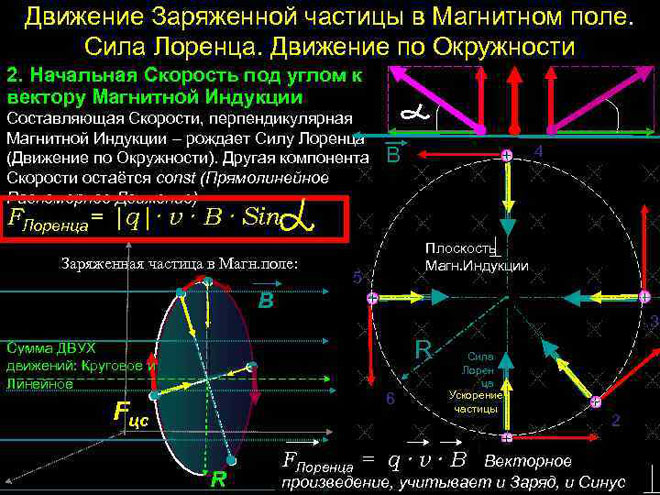
Varatun hiukkasen liike magneettikentässä

Yksinkertaisimmassa tapauksessa, eli kun magneettisen induktion ja hiukkasen nopeuden vektorit ovat kohtisuorassa, Lorentzin voima, joka on kohtisuorassa nopeusvektoriin nähden, voi ainoastaan muuttaa sen suuntaa. Nopeuden suuruus, siis energia, pysyy muuttumattomana. Lorentz-voima toimii siis analogisesti mekaniikan keskipakovoiman kanssa, ja hiukkanen liikkuu ympyrää pitkin.

Lue myös: Kuinka monta wattia on kilowatissa?

Newtonin toisen lain ( $F = m\cdot a$ ) voidaan määrittää hiukkasen pyörimissäde:

$N = \frac {m\cdot v}{q\cdot B}$ .

On huomattava, että hiukkasen ominaisvarauksen muuttuessa ( $\frac {q}{m}$ ) myös säde muuttuu.

Näin ollen kiertoaika T = . $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Se ei riipu nopeudesta, joten eri nopeuksilla liikkuvien hiukkasten keskinäinen sijainti on sama.

Varatun hiukkasen liike homogeenisessa magneettikentässä.

Monimutkaisemmassa tapauksessa, kun hiukkasen nopeuden ja magneettikentän voimakkuuden välinen kulma on mielivaltainen, hiukkanen liikkuu kierteistä rataa pitkin - asteittain kentän suuntaisen nopeuskomponentin kustannuksella ja kehän suuntaisesti sen kohtisuoran komponentin vaikutuksesta.

Lorentzin voiman sovellukset tekniikassa

Kineskooppi

Kineskooppi, joka oli viime aikoihin asti, jolloin se korvattiin LCD-näytöllä (litteällä näytöllä), joka oli jokaisessa televisiossa, ei olisi voinut toimia ilman Lorentzin voimaa. Televisiokuvan muodostamiseksi kuvaruudulle kapea elektronivirta on poikkeutuskeloja, jotka tuottavat lineaarisesti vaihtelevan magneettikentän. Viivakelat liikuttavat elektronisuihkua vasemmalta oikealle ja takaisin, kun taas runkokelat vastaavat pystysuuntaisesta liikkeestä ja liikuttavat juoksevaa sädettä vaakasuunnassa ylhäältä alas. Samaa periaatetta käytetään oskilloskoopit - välineet, joita käytetään sähköisten vaihtojännitteiden tutkimiseen.

Massaspektrografi

Massaspektrografi on laite, joka käyttää hyväksi varatun hiukkasen pyörimissäteen ja sen ominaisvarauksen välistä suhdetta. Sen toimintaperiaate on seuraava:

Varattujen hiukkasten lähde, joka saa nopeutta keinotekoisesti luodun sähkökentän avulla, sijoitetaan tyhjiökammioon ilmamolekyylien vaikutuksen poistamiseksi. Hiukkaset lentävät ulos lähteestä ja osuvat ympyrän kaarta pitkin valokuvauslevylle jättäen siihen jälkiä. Erityispanoksesta riippuen lentoradan säde ja siten myös iskeytymispiste muuttuvat. Tämä säde on helppo mitata, ja kun se tiedetään, hiukkasen massa voidaan laskea. Massaspektrografilla on tutkittu esimerkiksi kuun maaperän koostumusta.

Lue myös: Mitkä ovat sähköön liittyvät ammatit

Syklotroni

Varatun hiukkasen jakson ja siten sen pyörimistaajuuden riippumattomuutta sen nopeudesta magneettikentän läsnä ollessa käytetään syklotroniksi kutsutussa laitteessa, joka on suunniteltu kiihdyttämään hiukkasia suuriin nopeuksiin. Syklotroni koostuu kahdesta ontosta metallisesta puolisylinteristä, duanteista (kukin latinalaisen D-kirjaimen muotoinen), jotka asetetaan siten, että niiden suorat sivut ovat vastakkain lyhyen etäisyyden päässä toisistaan.

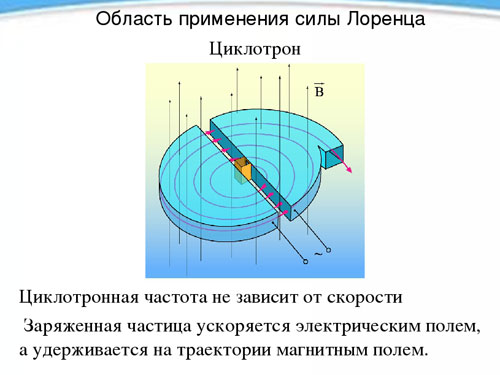
Syklotroni - Lorentzin voiman soveltaminen.

Duantit sijoitetaan vakioiseen homogeeniseen magneettikenttään, ja niiden välille luodaan vaihteleva sähkökenttä, jonka taajuus on yhtä suuri kuin hiukkasen pyörimistaajuus, joka määräytyy magneettikentän voimakkuuden ja ominaisvarauksen mukaan. Koska sähkökenttä vaikuttaa hiukkaseen kahdesti pyörimisjakson aikana (siirryttäessä duanttikappaleesta toiseen), se kiihtyy joka kerta, jolloin sen lentoradan säde kasvaa, ja kun se on saavuttanut tarvittavan nopeuden, se lentää tietyllä hetkellä ulos laitteesta reiän läpi. Tällä tavoin voidaan kiihdyttää protoni 20 MeV:n energiaan.megaelektronvolttia).

Magnetron

Magnetroniksi kutsuttu laite, joka on asennettu jokaiseen tietokoneeseen. mikroaaltouunion toinen esimerkki laitteesta, joka toimii Lorentzin voiman avulla. Magnetroni luo voimakkaan mikroaaltokentän, joka lämmittää uunin sisätilaa, johon ruoka asetetaan. Magnetronin magneetit säätävät elektronien kulkua uunin sisällä.

Maan magneettikenttä

Luonnossa Lorentzin voima on erittäin tärkeä ihmiskunnan kannalta. Sen ansiosta maapallon magneettikenttä voi suojella ihmisiä avaruuden tappavalta ionisoivalta säteilyltä. Kenttä estää varattuja hiukkasia pommittamasta planeetan pintaa ja pakottaa ne muuttamaan suuntaa.

Aiheeseen liittyvät artikkelit: