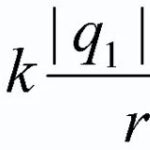Mikä on potentiaali ja potentiaaliero kahden pisteen välillä

Sähköpotentiaalin käsite on tärkeä perusta sähköstatiikan ja elektrodynamiikan teorialle. Sen olemuksen ymmärtäminen on edellytys näiden fysiikan alojen jatkotutkimukselle.

Mikä on sähköinen potentiaali

Olkoon yksikkövaraus q sijoitettu kenttään, jonka luo paikallaan oleva varaus Q, johon vaikuttavat seuraavat tekijät Coulombin voima F=k*Qq/r.

Jäljempänä k=((1/4)*π* ε* ε), jossa ε_{0 —} on sähköinen vakio (8,85*10^-12 F/m) ja ε väliaineen dielektrisyysvakio.

Esittänyt maksu voi liikkua tämän voiman vaikutuksesta, ja voima tekee tällöin jonkin verran työtä. Tämä tarkoittaa sitä, että kahden varauksen systeemillä on potentiaalienergia, joka riippuu molempien varausten suuruudesta ja niiden välisestä etäisyydestä, ja tämän potentiaalienergian suuruus on riippumaton varauksen q suuruudesta. Tässä yhteydessä otetaan käyttöön sähköpotentiaalin määritelmä - se on yhtä suuri kuin kentän potentiaalienergian ja varauksen suuruuden suhde:

φ = W/q,

jossa W on varausjärjestelmän luoman kentän potentiaalienergia, ja potentiaali on kentälle ominainen energia. Jotta varaus q voisi liikkua sähkökentässä jonkin matkan, on käytettävä jonkin verran työtä Coulombin voiman voittamiseksi. Pisteen potentiaali on yhtä suuri kuin työ, joka tarvitaan yksikkövarauksen siirtämiseksi pisteestä äärettömään. On huomattava, että:

• tämä työ on yhtä suuri kuin varauksen potentiaalienergian menetys (A=W).₂-W₁);
• työ on riippumaton varauksen liikeradasta.

SI-järjestelmässä potentiaalin yksikkö on yksi voltti (venäjänkielisessä kirjallisuudessa V, ulkomaisessa kirjallisuudessa V). 1 V=1J/1Kl, eli voimme puhua pisteen potentiaalista 1 voltin suuruisena, jos 1 Joulen työ tarvitaan 1 Joulen verran 1Kl:n varauksen siirtämiseksi äärettömään. Nimi on valittu italialaisen fyysikon Alessandro Voltan mukaan, joka vaikutti merkittävästi sähkötekniikan kehitykseen.

Potentiaalin havainnollistamiseksi sitä voidaan verrata kahden kappaleen lämpötilaan tai avaruuden eri pisteissä mitattuun lämpötilaan. Lämpötila mittaa kappaleiden lämpenemistä ja potentiaali mittaa sähkövarausta. Sanotaan, että yksi kappale lämpenee enemmän kuin toinen; voidaan myös sanoa, että toinen kappale on enemmän ja toinen vähemmän varautunut. Näillä elimillä on erilaisia mahdollisuuksia.

Potentiaalin arvo riippuu koordinaattijärjestelmän valinnasta, joten jokin taso on otettava nollaksi. Lämpötilaa mitattaessa vertailurajaksi voidaan ottaa esimerkiksi sulavan jään lämpötila. Potentiaalin osalta äärettömän kaukana sijaitsevan pisteen potentiaali on yleensä nolla, mutta joissakin sovelluksissa esimerkiksi maan potentiaali tai kondensaattorin yhden liittimen potentiaali voidaan ottaa nollaksi.

Potentiaalin ominaisuudet

Potentiaalin tärkeitä ominaisuuksia ovat

• jos kentän synnyttävät useat varaukset, potentiaali tietyssä pisteessä on yhtä suuri kuin kunkin varauksen synnyttämien potentiaalien algebrallinen (varauksen merkki huomioon ottaen) summa φ=φ₁+φ₂+φ₃+φ₄+φ₅+...+φ_n;
• jos etäisyydet varauksista ovat sellaiset, että itse varauksia voidaan pitää pistemäisinä, kokonaispotentiaali lasketaan kaavalla φ=k*(q₁/r₁+q₂/r₂+q₃/r₃+...+q_n/r_n), jossa r on etäisyys vastaavasta varauksesta kyseiseen pisteeseen.

Jos kentän muodostaa sähköinen dipoli (kaksi toisiinsa liittyvää vastakkaisenmerkkistä varausta), potentiaali missä tahansa pisteessä, joka sijaitsee etäisyydellä r dipolista, on φ=k*p*cosά/r.²missä:

• p on dipolin sähköinen varsi, joka on yhtä suuri kuin q*l, jossa l on varausten välinen etäisyys;
• r on etäisyys dipoliin;
• ά on dipolivarren ja sädevektorin r välinen kulma.

Jos piste sijaitsee dipoliakselilla, cosά=1 ja φ=k*p/r².

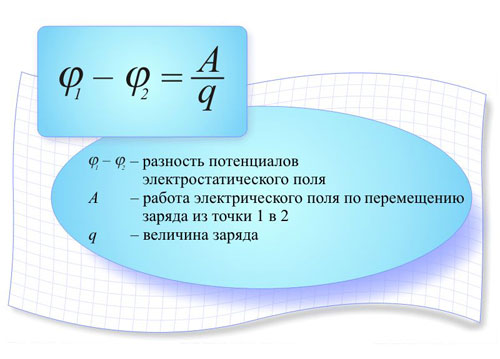
Potentiaaliero

Jos kahdella pisteellä on tietty potentiaali ja jos ne eivät ole yhtä suuret, sanotaan, että näiden kahden pisteen välillä on potentiaaliero. Pisteiden välillä on potentiaaliero

• jonka potentiaalin määräävät eri merkkiset varaukset;
• piste, jonka potentiaali on mistä tahansa varauksen merkistä, ja piste, jonka potentiaali on nolla.
• pisteitä, joiden potentiaali on samanmerkkinen mutta moduloiltaan erilainen.

Toisin sanoen potentiaaliero ei riipu koordinaattijärjestelmän valinnasta. Vertailukohtana voidaan käyttää vesialtaita, jotka sijaitsevat eri korkeuksilla maanpinnasta (esim. merenpinnasta).

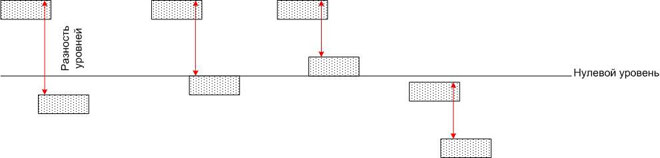
Kunkin altaan vedellä on tietty potentiaalienergia, mutta jos kaksi mitä tahansa allasta yhdistetään putkella, kumpaankin altaaseen virtaa vettä, jonka virtauksen määrää putken koon lisäksi myös potentiaalienergioiden ero maan vetovoimakentässä (eli korkeuserot). Potentiaalienergioiden absoluuttisella arvolla ei tässä tapauksessa ole merkitystä.

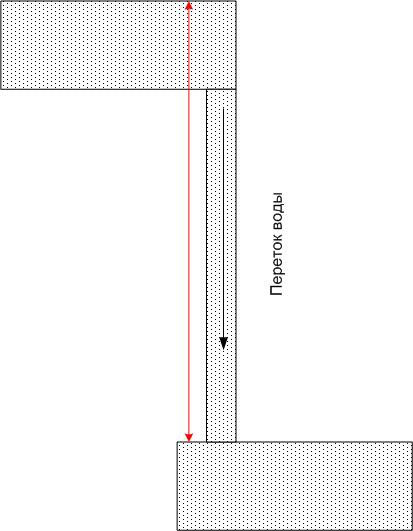
Vastaavasti, jos yhdistät kaksi pistettä, joilla on eri potentiaali, johtimella, se kantaa sähkövirtamääräytyy johtimen resistanssin lisäksi myös potentiaalieron mukaan (mutta ei sen absoluuttisen arvon mukaan). Jatkamalla vesivertailua voimme sanoa, että vesi yläaltaassa loppuu pian, ja ellei löydy voimaa, joka siirtää vettä takaisin ylöspäin (esimerkiksi pumppu), virtaus loppuu hyvin nopeasti.

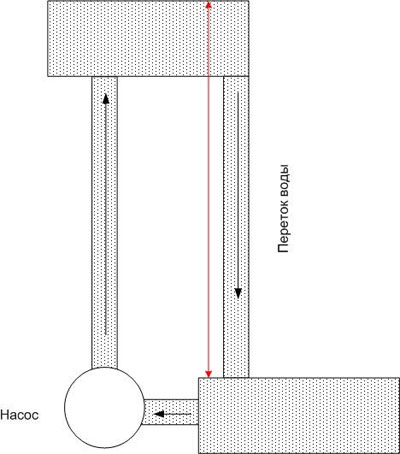
Sama pätee sähköpiirissä - jotta potentiaaliero pysyisi tietyllä tasolla, tarvitaan voima, joka kuljettaa varauksia (tai pikemminkin varauksenkuljettajia) pisteeseen, jossa on korkein potentiaali. Tätä voimaa kutsutaan sähkömotoriseksi voimaksi, ja siitä käytetään lyhennettä EMF. Sähkömagneettiset kentät voivat olla luonteeltaan erilaisia - sähkökemiallisia, sähkömagneettisia jne.

Käytännössä merkitystä on lähinnä varauksenkuljettajien liikeradan alkupisteen ja loppupisteen välisellä potentiaalierolla. Tässä tapauksessa tätä eroa kutsutaan jännitteeksi, ja SI-järjestelmässä se mitataan myös voltteina. Voidaan sanoa, että jännite on 1 voltti, jos kenttä tekee 1 Joulen verran työtä siirtäessään 1 Coulombin suuruista varausta pisteestä toiseen, eli 1V=1J/1Kl, ja J/Kl voi olla myös potentiaalieron mittayksikkö.

Ekvipotentiaalipinnat

Jos useiden pisteiden potentiaali on sama ja nämä pisteet muodostavat pinnan, tällaista pintaa kutsutaan ekvipotentiaaliseksi. Esimerkiksi sähkövarauksen ympärillä olevalla pallolla on tämä ominaisuus, koska sähkökenttä pienenee yhtä paljon kaikkiin suuntiin etäisyyden kasvaessa.

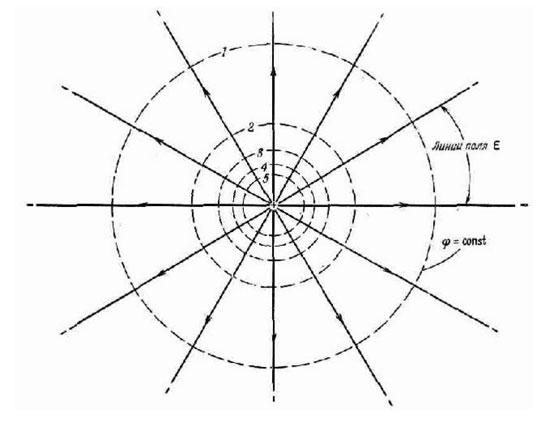
Kaikilla tämän pinnan pisteillä on sama potentiaalienergia, joten varauksen liikuttamiseen tällaisella pallolla ei kulu työtä. Usean varauksen järjestelmien ekvipotentiaalipinnat ovat muodoltaan monimutkaisempia, mutta niillä on yksi mielenkiintoinen ominaisuus - ne eivät koskaan leikkaa toisiaan. Sähkökentän voimaviivat ovat aina kohtisuorassa pintoihin nähden, joiden jokaisessa pisteessä on sama potentiaali. Jos ekvipotentiaalipinta leikataan tasossa, saadaan yhtäläisten potentiaalien viiva. Sillä on samat ominaisuudet kuin ekvipotentiaalipinnalla. Käytännössä esimerkiksi sähköstaattiseen kenttään sijoitetun johtimen pinnalla olevilla pisteillä on sama potentiaali.

Kun olet ymmärtänyt potentiaalin ja potentiaalieron käsitteen, voit alkaa oppia lisää sähköisistä ilmiöistä. Mutta ei ennen sitä, sillä ilman perusperiaatteiden ja -käsitteiden ymmärtämistä ei ole mahdollista syventää tietämystäsi.

Aiheeseen liittyvät artikkelit: