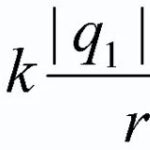La fuerza de Lorentz y la regla de la mano izquierda. Movimiento de partículas cargadas en un campo magnético

Un conductor colocado en un campo magnético conductora través del cual una corriente eléctrica una corriente eléctricase ve afectado por la fuerza de los amperios $F_A$ y su magnitud puede calcularse mediante la siguiente fórmula

$F_A=B\cdot I\cdot l\cdot sin\cpha$ (1)

donde $I$ и $l$ - el amperaje y la longitud del conductor, $B$ - la inducción del campo magnético, $\N - Alfa$ - el ángulo entre las direcciones de la corriente y la inducción magnética. Entonces, ¿por qué ocurre esto?

Fuerza de Lorentz. Movimiento de una partícula cargada en un campo magnético.

Contenido

1 Qué es la fuerza de Lorentz - definición, cuándo se produce, obtención de la fórmula
2 Determinación de la dirección de la fuerza de Lorentz mediante la regla de la mano izquierda
3 Movimiento de una partícula cargada en un campo magnético
4 Aplicación de la fuerza de Lorentz en la ingeniería

Qué es la fuerza de Lorentz - definición, cuándo surge, derivación de la fórmula

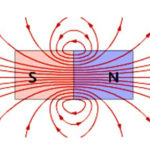
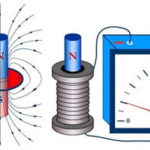
Se sabe que la corriente eléctrica es el movimiento ordenado de partículas cargadas. También se sabe que, al moverse en un campo magnético, cada una de estas partículas está sometida a una fuerza. Para que se produzca una fuerza, una partícula debe estar en movimiento.

La fuerza de Lorentz es la fuerza que actúa sobre una partícula cargada eléctricamente cuando se mueve en un campo magnético. Su dirección es ortogonal al plano en el que se encuentran los vectores de velocidad de la partícula y la intensidad del campo magnético. La fuerza de Lorentz es la fuerza de Ampere. Conociéndola, se puede derivar la fórmula de la fuerza de Lorentz.

El tiempo necesario para que una partícula atraviese una sección de un conductor, $t = \frac {l}{v}$ donde $l$ - es la longitud del segmento, $v$ - velocidad de la partícula. La carga total transportada durante este tiempo a través de la sección transversal del conductor, $Q = I\cdot t$ . Sustituyendo aquí el valor del tiempo de la ecuación anterior, tenemos

$Q = \frac {I\cdot l}{v}$ (2)

Al mismo tiempo $F_A = F_L\\cdot N$ donde $N$ - es el número de partículas en el conductor considerado. Al mismo tiempo $N = \frac {Q}{q}$ donde $q$ - es la carga de una partícula. Sustituyendo en la fórmula $Q$ de (2), se puede obtener:

$N = \frac {I\cdot l}{v\cdot q}$

Así,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Utilizando (1), la expresión anterior puede escribirse como

$B\cdot I\cdot l\cdot sin\cpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Tras los cortes y transferencias obtenemos la fórmula para el cálculo de la fuerza de Lorentz

$F_L = q\cdot v\cdot B\cdot sin\cpha$

Dado que la fórmula está escrita para un módulo de fuerza, debería escribirse como sigue:

Lea también: ¿Cómo convertir los amperios en vatios y viceversa?

$F_L = |q||\cdot v\cdot B\cdot sin\alpha$ (3)

Desde $sin\a alfa = sin(180^{circ} - \a alfa)$ , no importa para el cálculo del módulo de Lorentz si la velocidad está en la dirección de la corriente o en contra de ella, y podemos decir que $\N - Alfa$ - es el ángulo formado por los vectores de velocidad de la partícula y la inducción magnética.

Si escribes la fórmula en forma de vector, será así:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\\a veces \vec{B}]$ - es el producto vectorial, cuyo resultado es un vector con módulo igual a $v\cdot B\cdot sin\cpha$ .

De la fórmula (3) podemos concluir que la fuerza de Lorentz es máxima en el caso de perpendicularidad de las direcciones de la corriente eléctrica y del campo magnético, es decir, en $\N - alfa = 90^{circ}$ y desaparecerá en su paralelismo ( $\N - alfa = 0^{\\\N-circ}$ ).

Hay que recordar que para dar una respuesta cuantitativa correcta -por ejemplo en la resolución de problemas- hay que utilizar las unidades del SI, en las que la inducción magnética se mide en teslas (1 Tesla = 1 kg-c⁻²-А⁻¹), fuerza en newton (1 N = 1 kg-m/s²), corriente en amperios, carga en culones (1 Cl = 1 A-s), longitud en metros, velocidad en m/s.

Determinación de la dirección de la fuerza de Lorentz mediante la regla de la mano izquierda

Como en el mundo de los macroobjetos la fuerza de Lorentz se manifiesta como una fuerza de Ampere, podemos utilizar la regla de la mano izquierda para encontrar su dirección.

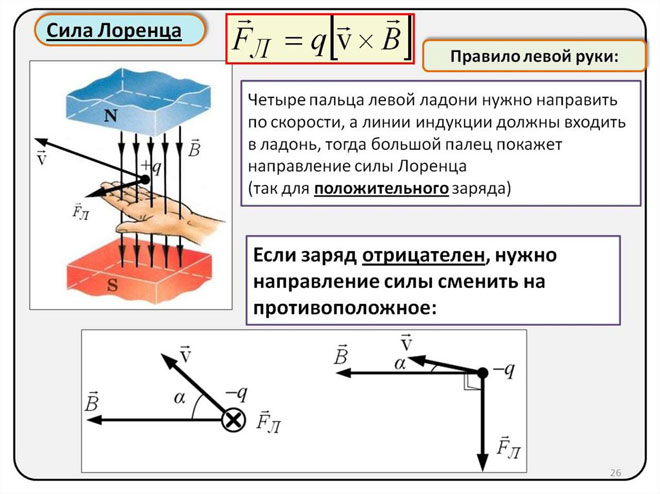
Determinación de la dirección de la fuerza de Lorentz mediante la regla de la mano izquierda.

Con la mano izquierda colocada perpendicularmente y de cara a las líneas del campo magnético, los cuatro dedos deben estar extendidos en la dirección de la corriente, entonces la fuerza de Lorentz se dirigirá hacia donde apunte el pulgar, que debe estar doblado.

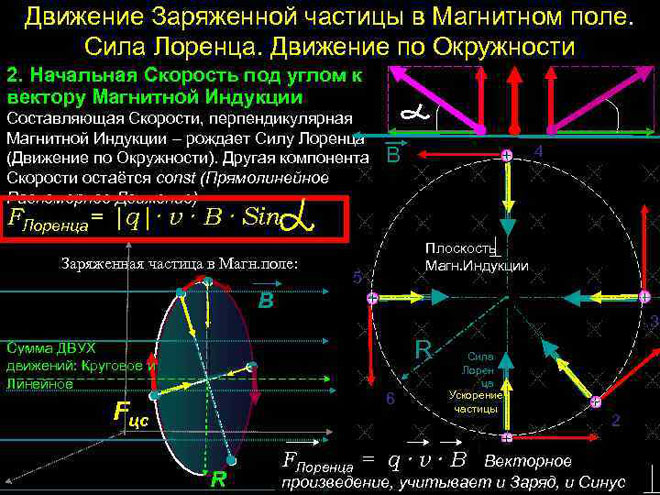
Movimiento de una partícula cargada en un campo magnético

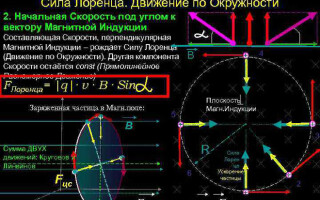
En el caso más sencillo, es decir, con ortogonalidad de los vectores de inducción magnética y velocidad de la partícula, la fuerza de Lorentz al ser perpendicular al vector velocidad, sólo puede cambiar su dirección. La magnitud de la velocidad, por lo tanto, la energía permanecerá inalterada. Así, la fuerza de Lorentz actúa por analogía con la fuerza centrípeta en mecánica y la partícula se mueve en un círculo.

Lea también: ¿Cuántos vatios hay en un kilovatio?

Según la segunda ley de Newton ( $F = m\cdot a$ ) se puede determinar el radio de rotación de una partícula:

$N = \frac {m\cdot v}{q\cdot B}$ .

Hay que tener en cuenta que al cambiar la carga específica de la partícula ( $\frac {q}{m}$ ) el radio también cambia.

Por tanto, el periodo de rotación T = . $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . No depende de la velocidad, por lo que la posición mutua de partículas con diferentes velocidades será la misma.

El movimiento de una partícula cargada en un campo magnético homogéneo.

En el caso más complicado, cuando el ángulo entre la velocidad de la partícula y la intensidad del campo magnético es arbitrario, se moverá a lo largo de una trayectoria helicoidal - progresivamente a expensas de la componente de la velocidad dirigida paralelamente al campo, y circunferencialmente a la influencia de su componente perpendicular.

Aplicaciones de la fuerza de Lorentz en la ingeniería

Cinescopio

El cinescopio, que hasta hace poco, cuando fue sustituido por el LCD (pantalla plana), estaba en todos los televisores, no podría haber funcionado sin la fuerza de Lorentz. Para formar una imagen de televisión en la pantalla, un estrecho chorro de electrones es desviado por bobinas que generan un campo magnético que varía linealmente. Las bobinas de línea mueven el haz de electrones de izquierda a derecha y viceversa, las bobinas de bastidor son responsables del movimiento vertical, moviendo el haz en marcha horizontalmente de arriba a abajo. El mismo principio se utiliza en osciloscopios - instrumentos utilizados para estudiar las tensiones eléctricas alternas.

Espectrógrafo de masas

Un espectrógrafo de masas es un instrumento que utiliza la relación entre el radio de rotación de una partícula cargada y su carga específica. Su principio de funcionamiento es el siguiente:

Una fuente de partículas cargadas, que adquieren velocidad mediante un campo eléctrico creado artificialmente, se coloca en una cámara de vacío para eliminar la influencia de las moléculas de aire. Las partículas salen volando de la fuente y, siguiendo un arco de círculo, chocan con una placa fotográfica, dejando huellas en ella. Dependiendo de la carga específica, cambia el radio de la trayectoria y, por tanto, el punto de impacto. Este radio es fácil de medir y, conociéndolo, se puede calcular la masa de la partícula. Mediante un espectrógrafo de masas, por ejemplo, se ha estudiado la composición del suelo lunar.

Lea también: ¿Cuáles son las profesiones relacionadas con la electricidad?

Ciclotrón

La independencia del periodo y, por tanto, de la frecuencia de rotación de una partícula cargada respecto a su velocidad en presencia de un campo magnético se utiliza en un aparato llamado ciclotrón, diseñado para acelerar partículas a altas velocidades. El ciclotrón consta de dos semicilindros metálicos huecos, duantes (cada una con forma de letra latina D), colocados con sus lados rectos enfrentados a corta distancia.

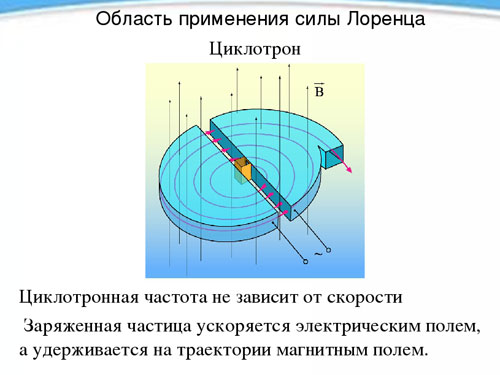
Ciclotrón - aplicación de la fuerza de Lorentz.

Los duantes se colocan en un campo magnético homogéneo constante, y entre ellos se crea un campo eléctrico alterno, cuya frecuencia es igual a la frecuencia de rotación de la partícula, determinada por la intensidad del campo magnético y la carga específica. Al estar influenciada por el campo eléctrico dos veces durante el periodo de rotación (al pasar de un duante a otro), la partícula se acelera cada vez, aumentando así el radio de la trayectoria, y en un momento dado, habiendo ganado la velocidad necesaria, sale volando del dispositivo a través del agujero. De esta manera se puede acelerar un protón hasta una energía de 20 MeVmega electronvoltio).

Magnetrón

Un dispositivo llamado magnetrón, que se instala en cada horno microondases otro ejemplo de aparato que funciona utilizando la fuerza de Lorentz. El magnetrón crea un fuerte campo de microondas que calienta el volumen interno del horno en el que se colocan los alimentos. Los imanes del magnetrón ajustan la trayectoria de los electrones dentro del horno.

El campo magnético de la Tierra

En la naturaleza, la fuerza de Lorentz es muy importante para la humanidad. Su presencia permite que el campo magnético de la Tierra proteja a los seres humanos de la mortífera radiación ionizante del espacio. El campo impide que las partículas cargadas bombardeen la superficie del planeta, obligándolas a cambiar de dirección.