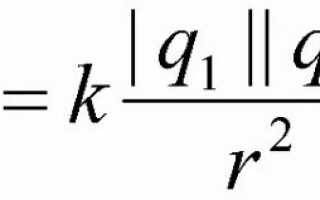চার্জযুক্ত দেহগুলির মধ্যে একটি মিথস্ক্রিয়া শক্তি রয়েছে, যার মাধ্যমে তারা একে অপরকে আকর্ষণ বা বিকর্ষণ করতে পারে। কুলম্বের আইন এই শক্তিকে বর্ণনা করে এবং শরীরের আকার এবং আকৃতির উপর নির্ভর করে এর প্রভাবের পরিমাণ দেখায়। এই শারীরিক আইন এই নিবন্ধে আলোচনা করা হবে.
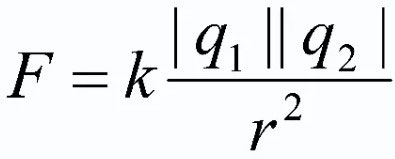
বিষয়বস্তু
স্থির পয়েন্ট চার্জ
কুলম্বের নিয়ম স্থির দেহগুলির ক্ষেত্রে প্রযোজ্য যেগুলির আকার অন্যান্য বস্তু থেকে তাদের দূরত্বের তুলনায় অনেক ছোট। এই ধরনের শরীরের উপর কেন্দ্রীভূত একটি বিন্দু বৈদ্যুতিক চার্জ আছে। শারীরিক সমস্যাগুলি সমাধান করার সময়, প্রশ্নে থাকা দেহের আকারগুলিকে উপেক্ষা করা হয়, কারণ সেগুলি খুব বেশি গুরুত্বপূর্ণ নয়।
অনুশীলনে, বিশ্রামের পয়েন্ট চার্জগুলি নিম্নরূপ চিত্রিত করা হয়েছে:


এই ক্ষেত্রে q1 এবং q2 - হয় ইতিবাচক বৈদ্যুতিক চার্জ, এবং কুলম্ব বল তাদের উপর কাজ করে (চিত্রে দেখানো হয়নি)। বিন্দু বস্তুর আকার কোন ব্যাপার না.
বিঃদ্রঃ! বিশ্রামের চার্জগুলি একে অপরের থেকে একটি নির্দিষ্ট দূরত্বে অবস্থিত, যা সমস্যাগুলিতে সাধারণত r অক্ষর দ্বারা চিহ্নিত করা হয়। আরও কাগজে আমরা এই চার্জগুলিকে ভ্যাকুয়ামে বিবেচনা করব।
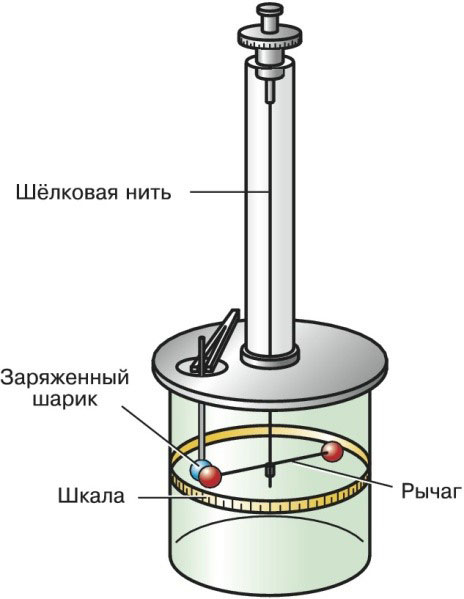
চার্লস কুলম্বের টর্শন স্কেল
1777 সালে কুলম্ব দ্বারা তৈরি এই ডিভাইসটি শক্তির নির্ভরতা অর্জনে সহায়তা করেছিল, পরে তার নামকরণ করা হয়েছিল। এটি পয়েন্ট চার্জের পাশাপাশি চৌম্বকীয় মেরুগুলির মিথস্ক্রিয়া অধ্যয়ন করতে ব্যবহৃত হয়।
টর্শন স্কেলগুলিতে একটি ছোট রেশম থ্রেড থাকে, একটি উল্লম্ব সমতলে অবস্থিত, যার উপর একটি সুষম লিভার ঝুলে থাকে। লিভারের প্রান্তে পয়েন্ট চার্জ রয়েছে।
বাহ্যিক শক্তির ক্রিয়াকলাপের অধীনে, লিভারটি অনুভূমিকভাবে চলতে শুরু করে। থ্রেডের স্থিতিস্থাপক বল দ্বারা ভারসাম্য না হওয়া পর্যন্ত লিভারটি সমতলে চলে যাবে।
চলাচলের প্রক্রিয়ায়, লিভারটি একটি নির্দিষ্ট কোণ দ্বারা উল্লম্ব অক্ষ থেকে বিচ্যুত হয়। এটি d হিসাবে নেওয়া হয় এবং ঘূর্ণনের কোণ বলা হয়। এই পরামিতিটির মান জেনে, আপনি ঘটমান বাহিনীর টর্ক খুঁজে পেতে পারেন।
চার্লস কুলম্বের টর্সনাল স্কেলগুলি দেখতে নিম্নরূপ:
সমানুপাতিকতার সহগ k এবং তড়িৎ ধ্রুবক 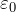
কুলম্বের সূত্রের পরামিতি k, সমানুপাতিকতার সহগ বা ![]() - বৈদ্যুতিক ধ্রুবক। বৈদ্যুতিক ধ্রুবক
- বৈদ্যুতিক ধ্রুবক। বৈদ্যুতিক ধ্রুবক ![]() অনেক রেফারেন্স বই, পাঠ্যপুস্তক, ইন্টারনেটে উপস্থাপন করা হয়, এবং এটি গণনা করার প্রয়োজন নেই! একটি ভ্যাকুয়ামে সমানুপাতিকতার সহগ উপর ভিত্তি করে
অনেক রেফারেন্স বই, পাঠ্যপুস্তক, ইন্টারনেটে উপস্থাপন করা হয়, এবং এটি গণনা করার প্রয়োজন নেই! একটি ভ্যাকুয়ামে সমানুপাতিকতার সহগ উপর ভিত্তি করে ![]() সুপরিচিত সূত্র ব্যবহার করে পাওয়া যাবে:
সুপরিচিত সূত্র ব্যবহার করে পাওয়া যাবে:
![]()
এখানে ![]() - বৈদ্যুতিক ধ্রুবক,
- বৈদ্যুতিক ধ্রুবক,
![]() - নম্বর পাই,
- নম্বর পাই,
![]() - ভ্যাকুয়ামে সমানুপাতিকতার সহগ।
- ভ্যাকুয়ামে সমানুপাতিকতার সহগ।
অতিরিক্ত তথ্য! উপরের প্যারামিটারগুলি না জেনে, দুটি বিন্দু বৈদ্যুতিক চার্জের মধ্যে মিথস্ক্রিয়া বল খুঁজে পাওয়া অসম্ভব।
কুলম্বের আইনের সূত্র এবং সূত্র
উপরের সংক্ষিপ্তসারের জন্য, ইলেক্ট্রোস্ট্যাটিক্সের প্রধান আইনের আনুষ্ঠানিক সূত্র দেওয়া প্রয়োজন। এটি ফর্ম নেয়:
একটি ভ্যাকুয়ামে দুটি বিশ্রাম বিন্দু চার্জের মিথস্ক্রিয়া বল এই চার্জগুলির গুণফলের সাথে সরাসরি সমানুপাতিক এবং তাদের মধ্যে দূরত্বের বর্গক্ষেত্রের বিপরীতভাবে সমানুপাতিক। আর পণ্যের চার্জ মডুলও নিতে হবে!
![]()
এই সূত্রে q1 এবং q2 - পয়েন্ট চার্জ, বিবেচিত সংস্থা; r2 - এই শরীরের মধ্যে একটি সমতলে দূরত্ব, একটি বর্গ হিসাবে নেওয়া হয়; k হল আনুপাতিকতার গুণনীয়ক (![]() ভ্যাকুয়ামের জন্য)।
ভ্যাকুয়ামের জন্য)।
কুলম্ব বলের দিক এবং সূত্রের ভেক্টর ফর্ম
সূত্রটি সম্পূর্ণরূপে বোঝার জন্য কুলম্বের আইনটি দৃশ্যত চিত্রিত করা যেতে পারে:
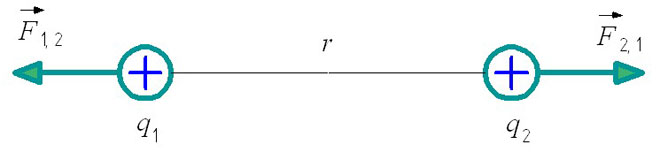
চ1,2 - দ্বিতীয় চার্জের সাপেক্ষে প্রথম চার্জের মিথস্ক্রিয়া বল।
চ2,1 - প্রথমটির সাপেক্ষে দ্বিতীয় চার্জের মিথস্ক্রিয়া বল।
এছাড়াও, ইলেক্ট্রোস্ট্যাটিক্স সমস্যাগুলি সমাধান করার সময়, একটি গুরুত্বপূর্ণ নিয়ম বিবেচনায় নেওয়া প্রয়োজন: একই-নামযুক্ত বৈদ্যুতিক চার্জগুলি বিকর্ষণ করে এবং বিপরীত নামযুক্ত চার্জগুলি আকর্ষণ করে। এটি চিত্রে মিথস্ক্রিয়া শক্তির অবস্থান নির্ধারণ করে।
যদি বিপরীত চার্জ বিবেচনা করা হয়, তাদের মিথস্ক্রিয়া শক্তিগুলি একে অপরের দিকে পরিচালিত হবে, তাদের আকর্ষণকে প্রতিনিধিত্ব করে।
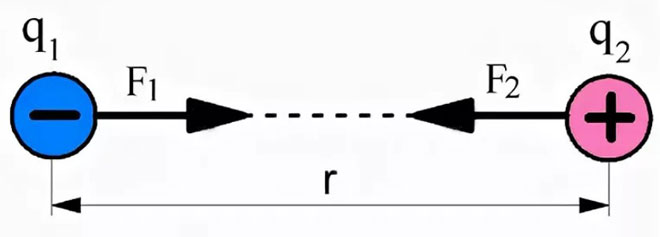
ভেক্টর আকারে ইলেক্ট্রোস্ট্যাটিক্সের মৌলিক আইনের সূত্রটি নিম্নরূপ উপস্থাপন করা যেতে পারে:
![]()
![]() - বিন্দু চার্জ q1, চার্জ q2 এর পাশে যে বল কাজ করে,
- বিন্দু চার্জ q1, চার্জ q2 এর পাশে যে বল কাজ করে,
![]() - ব্যাসার্ধ-ভেক্টর সংযোগকারী চার্জ q2 কে q1 চার্জ করে,
- ব্যাসার্ধ-ভেক্টর সংযোগকারী চার্জ q2 কে q1 চার্জ করে,
![]()
গুরুত্বপূর্ণ ! ভেক্টর আকারে সূত্রটি লেখার পরে, চিহ্নগুলিকে সঠিকভাবে স্থাপন করার জন্য দুটি বিন্দু বৈদ্যুতিক চার্জের মিথস্ক্রিয়া শক্তিগুলিকে অক্ষের উপর প্রক্ষিপ্ত করতে হবে। এই ক্রিয়াটি একটি আনুষ্ঠানিকতা এবং প্রায়শই কোনও নোট ছাড়াই মানসিকভাবে করা হয়।
যেখানে কুলম্বের আইন বাস্তবে প্রযোজ্য
ইলেক্ট্রোস্ট্যাটিক্সের মৌলিক আইন চার্লস কুলম্বের সবচেয়ে গুরুত্বপূর্ণ আবিষ্কার, যা অনেক ক্ষেত্রে এর প্রয়োগ খুঁজে পেয়েছে।
বিখ্যাত পদার্থবিজ্ঞানীর কাজটি বিভিন্ন যন্ত্র, যন্ত্র, যন্ত্রপাতি উদ্ভাবনের প্রক্রিয়ায় ব্যবহৃত হয়েছিল। যেমন বাজ রড।
বজ্রপাতের রড ব্যবহার করে, বজ্রপাতের সময় বাড়ি এবং ভবনগুলিকে বজ্রপাত থেকে রক্ষা করা হয়। এইভাবে, বৈদ্যুতিক সরঞ্জাম সুরক্ষা ডিগ্রী বৃদ্ধি করা হয়।
বজ্রপাতের রডগুলি নিম্নলিখিত নীতিতে কাজ করে: বজ্রঝড়ের সময় শক্তিশালী ইন্ডাকশন চার্জ ধীরে ধীরে মাটিতে জমা হয়, যা উপরে উঠে এবং মেঘের প্রতি আকৃষ্ট হয়। এটি মাটিতে একটি উল্লেখযোগ্য বৈদ্যুতিক ক্ষেত্র তৈরি করে। বজ্রপাতের রডের কাছে, বৈদ্যুতিক ক্ষেত্রটি শক্তিশালী হয়ে ওঠে, যাতে যন্ত্রের ডগা থেকে করোনা বৈদ্যুতিক চার্জ প্রজ্বলিত হয়।
তারপরে মাটিতে গঠিত চার্জ বিপরীত চিহ্ন সহ মেঘের আধানের প্রতি আকৃষ্ট হতে শুরু করে, যেমনটি চার্লস কুলম্বের আইন অনুসারে হওয়া উচিত। তারপর বায়ু আয়নিত হয়, এবং বৈদ্যুতিক ক্ষেত্রের শক্তি বজ্রের রডের শেষের কাছে কম হয়ে যায়। সুতরাং, ভবনে বজ্রপাতের ঝুঁকি ন্যূনতম।
দয়া করে নোট করুন! যদি বাজ রড সহ একটি বিল্ডিং আঘাত করে তবে সেখানে আগুন থাকবে না এবং সমস্ত শক্তি মাটিতে চলে যায়।
কুলম্বের আইনের উপর ভিত্তি করে, "পার্টিকেল অ্যাক্সিলারেটর" নামে একটি ডিভাইস তৈরি করা হয়েছিল এবং বর্তমানে এটির প্রচুর চাহিদা রয়েছে।
এই ডিভাইসটি একটি শক্তিশালী বৈদ্যুতিক ক্ষেত্র তৈরি করে, যা এতে প্রবেশকারী কণার শক্তি বৃদ্ধি করে।
কুলম্বের আইনে বাহিনীর দিকনির্দেশ
উপরে উল্লিখিত হিসাবে, দুটি বিন্দু বৈদ্যুতিক চার্জের মিথস্ক্রিয়া শক্তির দিক তাদের মেরুত্বের উপর নির্ভর করে। অর্থাৎ, একই-প্রতিবেশী চার্জ বিকর্ষণ করবে এবং বিপরীত-প্রতিবেশী চার্জ আকর্ষণ করবে।
কুলম্ব বলগুলিকে ব্যাসার্ধ-ভেক্টরও বলা যেতে পারে, কারণ তারা ব্যাসার্ধ-ভেক্টরের মতোই। তারা তাদের মধ্যে আঁকা একটি লাইন বরাবর নির্দেশিত হয়.
কিছু শারীরিক সমস্যায় জটিল আকৃতির দেহ থাকে, যেগুলিকে বিন্দু বৈদ্যুতিক চার্জ হিসাবে গ্রহণ করা যায় না, অর্থাৎ এর আকারকে অবহেলা করা। এই পরিস্থিতিতে, প্রশ্নে থাকা শরীরটিকে কয়েকটি ছোট অংশে ভাগ করা উচিত এবং কুলম্বের আইন প্রয়োগ করে প্রতিটি অংশ আলাদাভাবে গণনা করা উচিত।
বিভাজনে প্রাপ্ত বল ভেক্টরগুলি বীজগণিত এবং জ্যামিতির নিয়ম দ্বারা যোগ করা হয়। ফলাফল হল ফলের শক্তি, যা সমস্যার উত্তর হবে।সমাধানের এই পদ্ধতিটিকে প্রায়শই ত্রিভুজ পদ্ধতি হিসাবে উল্লেখ করা হয়।
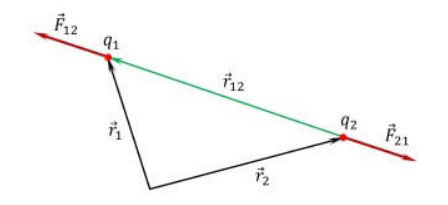
আইন আবিষ্কারের ইতিহাস
উপরে আলোচিত আইন দ্বারা দুটি পয়েন্ট চার্জের মিথস্ক্রিয়া প্রথম 1785 সালে চার্লস কুলম্ব দ্বারা প্রমাণিত হয়েছিল। পদার্থবিজ্ঞানী টর্শন স্কেল ব্যবহার করে প্রণীত আইনের সত্যতা প্রমাণ করতে পেরেছিলেন, যার অপারেশনের নীতিটি নিবন্ধে উপস্থাপিত হয়েছিল।
কুলম্ব আরও প্রমাণ করেছেন যে একটি গোলাকার ক্যাপাসিটরের ভিতরে কোন বৈদ্যুতিক চার্জ নেই। এভাবেই তিনি এই দাবীতে পৌঁছেছেন যে ইলেক্ট্রোস্ট্যাটিক শক্তির মাত্রা প্রশ্নে থাকা দেহগুলির মধ্যে দূরত্ব পরিবর্তন করে পরিবর্তন করা যেতে পারে।
এইভাবে, কুলম্বের সূত্র এখনও ইলেক্ট্রোস্ট্যাটিক্সের সবচেয়ে গুরুত্বপূর্ণ আইন, যার ভিত্তিতে অনেক বড় আবিষ্কার করা হয়েছে। এই নিবন্ধের মধ্যে, আইনের আনুষ্ঠানিক প্রণয়ন উপস্থাপন করা হয়েছে, এবং এর উপাদান অংশগুলি বিশদভাবে বর্ণনা করা হয়েছে।
সম্পরকিত প্রবন্ধ: