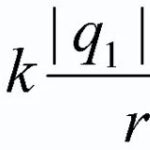দুটি বিন্দুর মধ্যে সম্ভাব্য এবং সম্ভাব্য পার্থক্য কী

বৈদ্যুতিক সম্ভাবনার ধারণাটি ইলেক্ট্রোস্ট্যাটিক্স এবং ইলেক্ট্রোডায়নামিক্স তত্ত্বের একটি গুরুত্বপূর্ণ ভিত্তি। পদার্থবিজ্ঞানের এই বিভাগগুলির আরও অধ্যয়নের জন্য এর সারাংশ বোঝা একটি পূর্বশর্ত।

বৈদ্যুতিক সম্ভাবনা কি

স্থির চার্জ Q দ্বারা সৃষ্ট ক্ষেত্রে একটি ইউনিট চার্জ q স্থাপন করা যাক, যার উপর কুলম্ব বল F=k*Qq/r

এর পরে k=((1/4)*π* ε* ε), যেখানে ε_{0 —} বৈদ্যুতিক ধ্রুবক (8.85*10^-12 F/m), এবং ε মাধ্যমের অস্তরক ধ্রুবক.

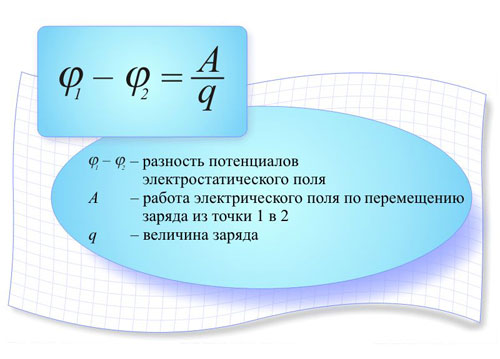
দ্বারা প্রবর্তিত চার্জ এই শক্তির কর্মের অধীনে নড়াচড়া করতে পারে, এবং বাহিনী কিছু কাজ করবে। এর মানে হল যে দুটি চার্জের একটি সিস্টেমে একটি সম্ভাব্য শক্তি রয়েছে যা উভয় চার্জের মাত্রা এবং তাদের মধ্যে দূরত্বের উপর নির্ভর করে এবং এই সম্ভাব্য শক্তির মান চার্জ q এর মাত্রার উপর নির্ভর করে না। এখানেই বৈদ্যুতিক সম্ভাবনার সংজ্ঞাটি চালু করা হয়েছে: এটি চার্জের মাত্রার সাথে ক্ষেত্রের সম্ভাব্য শক্তির অনুপাতের সমান:

φ=W/q,

যেখানে W হল চার্জ সিস্টেম দ্বারা সৃষ্ট ক্ষেত্রের সম্ভাব্য শক্তি, এবং সম্ভাব্য হল ক্ষেত্রের একটি শক্তি বৈশিষ্ট্য। একটি বৈদ্যুতিক ক্ষেত্রে একটি চার্জ q কিছু দূরত্বের জন্য সরানোর জন্য, কুলম্ব বলকে অতিক্রম করার জন্য কিছু কাজ ব্যয় করতে হবে।একটি বিন্দুর সম্ভাব্যতা একটি ইউনিট চার্জকে সেই বিন্দু থেকে অসীমে নিয়ে যেতে যে কাজটি লাগে তার সমান। এটা উল্লেখ করা উচিত যে:

• এই কাজটি চার্জের সম্ভাব্য শক্তির ক্ষতির সমান হবে (A=W₂-ডব্লিউ₁);
• কাজ চার্জের গতিপথের উপর নির্ভর করে না।

SI সিস্টেমে, সম্ভাব্যতার একক হল এক ভোল্ট (রাশিয়ান ভাষার সাহিত্যে V দ্বারা চিহ্নিত করা হয়, বিদেশী সাহিত্যে V)। 1 V=1J/1 Kl, অর্থাৎ, আমরা 1 ভোল্টের একটি বিন্দুর সম্ভাব্যতা সম্পর্কে কথা বলতে পারি, যদি 1 Kl চার্জকে অসীমে নিয়ে যেতে 1 জুলের কাজ লাগে। নামটি ইতালীয় পদার্থবিদ আলেসান্দ্রো ভোল্টার সম্মানে বেছে নেওয়া হয়েছিল, যিনি বৈদ্যুতিক প্রকৌশলের বিকাশে গুরুত্বপূর্ণ অবদান রেখেছিলেন।

সম্ভাব্যতা কী তা কল্পনা করতে, এটি দুটি দেহের তাপমাত্রা বা মহাকাশের বিভিন্ন বিন্দুতে পরিমাপ করা তাপমাত্রার সাথে তুলনা করা যেতে পারে। তাপমাত্রা হল বস্তুর উত্তাপের একটি পরিমাপ, এবং সম্ভাব্য বৈদ্যুতিক চার্জের একটি পরিমাপ। একটি শরীর অন্যটির চেয়ে বেশি উত্তপ্ত বলা হয় এবং এটিও বলা যেতে পারে যে একটি শরীর বেশি চার্জযুক্ত এবং অন্যটি কম চার্জযুক্ত। এই শরীরের বিভিন্ন সম্ভাবনা আছে.

সম্ভাব্যতার মান স্থানাঙ্ক ব্যবস্থার পছন্দের উপর নির্ভর করে, তাই কিছু স্তরকে শূন্য হিসাবে নেওয়া প্রয়োজন। তাপমাত্রা পরিমাপ করার সময়, কেউ নিতে পারে, উদাহরণস্বরূপ, একটি রেফারেন্স সীমানা হিসাবে বরফ গলে যাওয়ার তাপমাত্রা। একটি সম্ভাব্য জন্য, একটি অসীম দূরবর্তী বিন্দুর সম্ভাব্যতা সাধারণত শূন্য হিসাবে নেওয়া হয়, কিন্তু কিছু সমস্যার জন্য, পৃথিবীর সম্ভাব্যতা বা একটি ক্যাপাসিটরের কভারগুলির একটির সম্ভাব্যতা, উদাহরণস্বরূপ, শূন্য হিসাবে নেওয়া যেতে পারে।

সম্ভাবনার বৈশিষ্ট্য

একটি সম্ভাবনার গুরুত্বপূর্ণ বৈশিষ্ট্যগুলির মধ্যে নিম্নলিখিতগুলি হল:

• যদি ক্ষেত্রটি বেশ কয়েকটি চার্জ দ্বারা তৈরি করা হয়, তবে একটি নির্দিষ্ট বিন্দুতে সম্ভাব্যতা বীজগণিতের সমান হবে (চার্জের চিহ্নটি বিবেচনায় নিয়ে) প্রতিটি চার্জ দ্বারা সৃষ্ট সম্ভাব্যতার যোগফল φ=φ₁+φ₂+φ₃+φ₄+φ₅+...φ_n;
• যদি চার্জগুলি থেকে দূরত্ব এমন হয় যে চার্জগুলিকে বিন্দু-সদৃশ বিবেচনা করা যেতে পারে, তাহলে মোট সম্ভাব্যতা φ=k*(q) সূত্র দ্বারা গণনা করা হয়₁/আর₁+q₂/আর₂+q₃/আর₃+...q_n/আর_n), যেখানে r হল সংশ্লিষ্ট চার্জ থেকে প্রশ্নবিন্দুর দূরত্ব।

যদি ক্ষেত্রটি একটি বৈদ্যুতিক ডাইপোল (বিপরীত চিহ্নের দুটি সংযুক্ত চার্জ) দ্বারা গঠিত হয়, তাহলে ডাইপোল থেকে r দূরত্বে অবস্থিত যেকোনো বিন্দুতে সম্ভাব্য φ=k*p*cosά/r এর সমান হবে।², কোথায়:

• p হল ডাইপোলের বৈদ্যুতিক বাহু, q*l এর সমান, যেখানে l চার্জগুলির মধ্যে দূরত্ব;
• r হল ডাইপোলের দূরত্ব;
• ά হল ডাইপোল বাহু এবং ব্যাসার্ধ ভেক্টর r এর মধ্যবর্তী কোণ।

যদি বিন্দুটি ডাইপোল অক্ষের উপর থাকে, cosά=1 এবং φ=k*p/r².

সম্ভাব্য পার্থক্য

যদি দুটি বিন্দুর একটি নির্দিষ্ট সম্ভাবনা থাকে, এবং যদি তারা সমান না হয় তবে বলা হয় যে দুটি বিন্দুর মধ্যে একটি সম্ভাব্য পার্থক্য রয়েছে। পয়েন্টগুলির মধ্যে একটি সম্ভাব্য পার্থক্য ঘটে:

• যার সম্ভাব্যতা বিভিন্ন চিহ্নের চার্জ দ্বারা নির্ধারিত হয়;
• যে কোনো চিহ্নের চার্জ থেকে সম্ভাব্য একটি বিন্দু এবং শূন্য সম্ভাবনার একটি বিন্দু;
• পয়েন্টে সমান চিহ্নের সম্ভাবনা রয়েছে, কিন্তু মডুলোতে ভিন্ন।

অর্থাৎ, সম্ভাব্য পার্থক্য স্থানাঙ্ক ব্যবস্থার পছন্দের উপর নির্ভর করে না। আমরা শূন্য চিহ্নের (যেমন সমুদ্রপৃষ্ঠ) সাপেক্ষে বিভিন্ন উচ্চতায় অবস্থিত জলের পুলগুলির সাথে একটি সাদৃশ্য আঁকতে পারি।

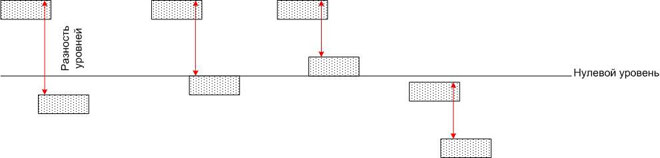
প্রতিটি পুলের জলের একটি নির্দিষ্ট সম্ভাব্য শক্তি রয়েছে, তবে আপনি যদি দুটি পুলকে একটি নল দিয়ে সংযুক্ত করেন, তবে তাদের প্রতিটিতে জলের প্রবাহ থাকবে, যার প্রবাহ কেবল নলের আকার দ্বারা নির্ধারিত হয় না, কিন্তু পৃথিবীর মহাকর্ষীয় ক্ষেত্রের সম্ভাব্য শক্তির পার্থক্য দ্বারাও (অর্থাৎ উচ্চতার পার্থক্য)। সম্ভাব্য শক্তির পরম মান এই ক্ষেত্রে কোন ব্যাপার না.

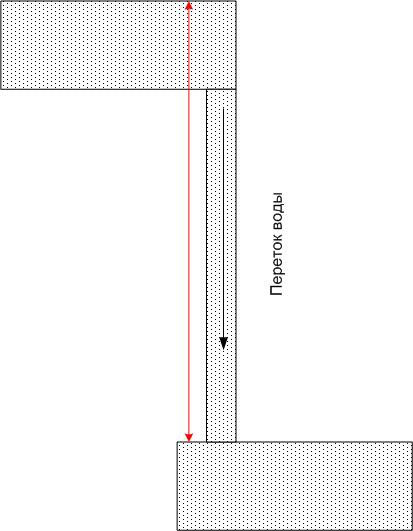
একইভাবে, যদি আপনি একটি কন্ডাক্টরকে দুটি বিন্দুর সাথে বিভিন্ন সম্ভাবনার সাথে সংযুক্ত করেন তবে এটি বহন করবে একটি বৈদ্যুতিক প্রবাহশুধুমাত্র কন্ডাক্টরের প্রতিরোধের দ্বারা নয়, সম্ভাব্য পার্থক্য দ্বারাও নির্ধারিত হয় (কিন্তু তাদের পরম মান দ্বারা নয়)। জলের সাদৃশ্য অব্যাহত রেখে, আমরা বলতে পারি যে উপরের বেসিনের জল শীঘ্রই ফুরিয়ে যাবে, এবং যদি জলকে আবার উপরে (যেমন একটি পাম্প) নিয়ে যাওয়ার জন্য কোনও জোর না থাকে তবে প্রবাহ খুব দ্রুত বন্ধ হয়ে যাবে।

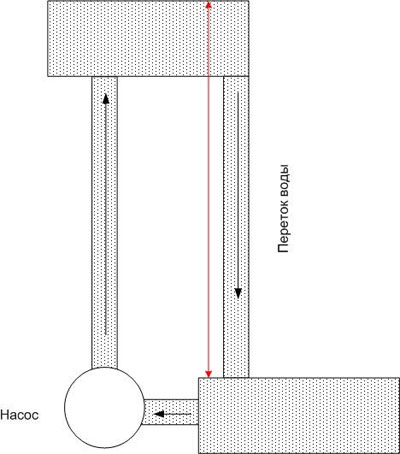
এটি একটি বৈদ্যুতিক সার্কিটে একই: একটি নির্দিষ্ট স্তরে সম্ভাব্য পার্থক্য রাখতে, একটি শক্তির প্রয়োজন হয় যা চার্জগুলিকে (অথবা বরং, চার্জ বাহকদের) সর্বোচ্চ সম্ভাবনা সহ বিন্দুতে পরিবহন করে। এই বলকে ইলেক্ট্রোমোটিভ ফোর্স বলা হয় এবং সংক্ষেপে ইএমএফ বলা হয়। EMF বিভিন্ন প্রকৃতির হতে পারে - ইলেক্ট্রোকেমিক্যাল, ইলেক্ট্রোম্যাগনেটিক ইত্যাদি।

অনুশীলনে, এটি প্রধানত চার্জ বাহকগুলির গতিপথের শুরু এবং শেষ বিন্দুর মধ্যে সম্ভাব্য পার্থক্য যা গুরুত্বপূর্ণ। এই ক্ষেত্রে, এই পার্থক্যটিকে ভোল্টেজ বলা হয় এবং এসআইতে এটি ভোল্টেও পরিমাপ করা হয়। 1 ভোল্টের একটি ভোল্টেজের কথা বলা যেতে পারে যদি ক্ষেত্রটি 1 কুলম্বের চার্জকে এক বিন্দু থেকে অন্য বিন্দুতে সরাতে 1 জুলের কাজ করে, অর্থাৎ 1V=1J/1KL, এবং J/KLও এর একক হতে পারে। সম্ভাব্য পার্থক্য.

Equipotential পৃষ্ঠতল

যদি বেশ কয়েকটি বিন্দুর সম্ভাব্যতা একই হয় এবং এই বিন্দুগুলি একটি পৃষ্ঠ তৈরি করে, তবে এই জাতীয় পৃষ্ঠকে সমতুল্য বলা হয়। উদাহরণস্বরূপ, বৈদ্যুতিক চার্জের চারপাশে ঘেরা একটি গোলকের এই বৈশিষ্ট্য রয়েছে, কারণ বৈদ্যুতিক ক্ষেত্র দূরত্বের সাথে সমস্ত দিকে সমানভাবে হ্রাস পায়।

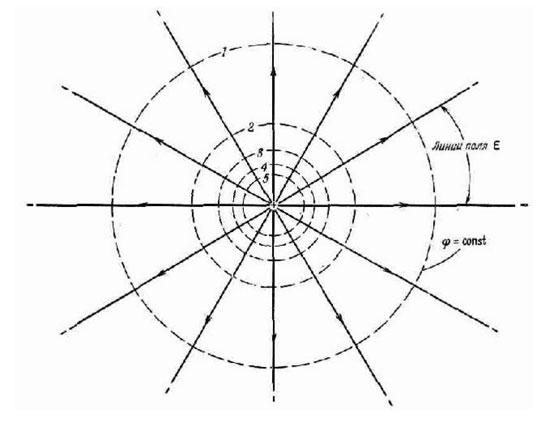
এই পৃষ্ঠের সমস্ত বিন্দুতে একই সম্ভাব্য শক্তি রয়েছে, তাই এই জাতীয় গোলকের উপর চার্জ সরানোর সময় কোনও কাজ ব্যয় করা হবে না। বেশ কয়েকটি চার্জের সিস্টেমের সমতুল্য পৃষ্ঠগুলির একটি আরও জটিল আকার রয়েছে, তবে তাদের একটি আকর্ষণীয় বৈশিষ্ট্য রয়েছে: তারা কখনই ছেদ করে না। বৈদ্যুতিক ক্ষেত্রের বলের রেখাগুলি সর্বদা তাদের প্রতিটি বিন্দুতে একই সম্ভাবনা সহ পৃষ্ঠের সাথে লম্ব থাকে। সমতলে সমতল দ্বারা ব্যবচ্ছেদ করা হলে, আপনি সমান সম্ভাবনার একটি লাইন পাবেন।এটির সমতুল্য পৃষ্ঠের মতো একই বৈশিষ্ট্য রয়েছে। অনুশীলনে, একটি ইলেক্ট্রোস্ট্যাটিক ক্ষেত্রের মধ্যে স্থাপিত একটি কন্ডাকটরের পৃষ্ঠের বিন্দু, উদাহরণস্বরূপ, সমান সম্ভাবনা রয়েছে।

একবার আপনি সম্ভাব্য এবং সম্ভাব্য পার্থক্যের ধারণাটি বুঝতে পারলে, আপনি আরও বৈদ্যুতিক ঘটনা অধ্যয়ন শুরু করতে পারেন। তবে আগে নয়, কারণ মৌলিক নীতি ও ধারণা না বুঝে জ্ঞানকে গভীর করা সম্ভব হবে না।

সম্পরকিত প্রবন্ধ: