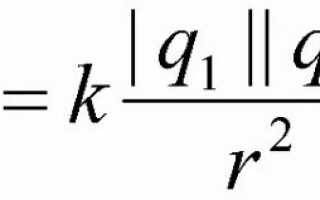Pomiędzy naładowanymi ciałami istnieje siła oddziaływania, dzięki której mogą się one przyciągać lub odpychać. Prawo Coulomba opisuje tę siłę i pokazuje, w jakim stopniu działa ona w zależności od wielkości i kształtu ciała. To prawo fizyczne zostanie omówione w niniejszym artykule.
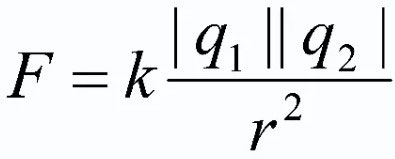
Spis treści
Stacjonarne opłaty punktowe
Prawo Coulomba ma zastosowanie do ciał nieruchomych, których rozmiary są znacznie mniejsze niż odległość od innych obiektów. Na takich ciałach znajduje się punktowy ładunek elektryczny. Przy rozwiązywaniu zadań fizycznych pomija się wymiary rozpatrywanych ciał, ponieważ nie mają one większego znaczenia.
W praktyce spoczywające ładunki punktowe przedstawia się w następujący sposób:
W tym przypadku q1 i q2 - są pozytywny ładunki elektryczne i działa na nie siła Coulomba (nie pokazana na rysunku). Rozmiar obiektów punktowych nie ma znaczenia.
Uwaga! Ładunki spoczywające znajdują się w określonej odległości od siebie, którą w zadaniach zwykle oznacza się literą r. W dalszej części opracowania zarzuty te zostaną rozpatrzone w warunkach próżni.
Skale torsyjne Charlesa Coulomba
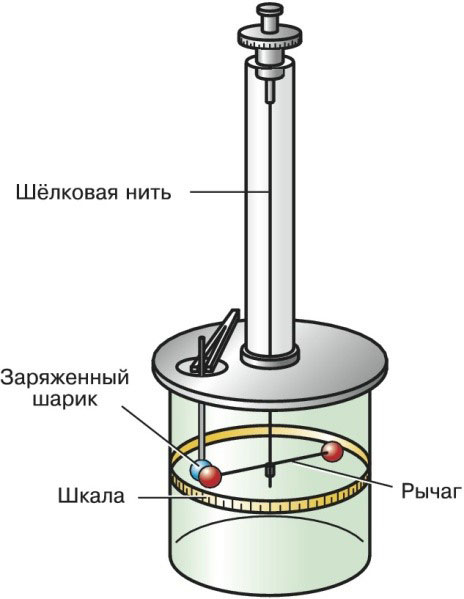
Aparat ten, skonstruowany przez Coulomba w 1777 roku, pomógł uzyskać zależność siły nazwanej później jego nazwiskiem. Służy do badania wzajemnego oddziaływania ładunków punktowych i biegunów magnetycznych.
Wagi skrętne mają małą jedwabną nić, umieszczoną w płaszczyźnie pionowej, na której zawieszona jest wyważona dźwignia. Na końcach dźwigni znajdują się ładunki punktowe.
Pod wpływem działania sił zewnętrznych dźwignia zaczyna wykonywać ruchy poziome. Dźwignia będzie poruszać się po płaszczyźnie, dopóki nie zostanie zrównoważona przez siłę sprężystości nici.
W trakcie ruchu dźwignia odchyla się od osi pionowej pod pewnym kątem. Wartość tę przyjmuje się jako d i nazywa się ona kątem obrotu. Znając wartość tego parametru, można znaleźć moment występujących sił.
Skale torsyjne Charlesa Coulomba wyglądają następująco:
Współczynnik proporcjonalności k i stała elektryczna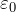 
Wzór na prawo Coulomba ma parametry k - współczynnik proporcjonalności lub - stała elektryczna. Stała elektryczna jest podawana w wielu źródłach informacji, podręcznikach, Internecie i nie trzeba jej obliczać! Współczynnik proporcjonalności w próżni na podstawie można znaleźć zgodnie z dobrze znanym wzorem:
Tutaj 
- stała elektryczna,
- liczba pi,
- to współczynnik proporcjonalności w próżni.
Więcej informacji! Bez znajomości powyższych parametrów nie jest możliwe znalezienie siły oddziaływania pomiędzy dwoma punktowymi ładunkami elektrycznymi.
Sformułowanie i wzór prawa Coulomba
Podsumowując powyższe rozważania, należy podać formalne sformułowanie głównego prawa elektrostatyki. Ma to postać:
Siła oddziaływania dwóch spoczywających w próżni ładunków punktowych jest wprost proporcjonalna do iloczynu tych ładunków i odwrotnie proporcjonalna do kwadratu odległości między nimi. A iloczyn ładunków musi być wzięty modulo!
W tym wzorze q1 i q2 - są ładunkami punktowymi, czyli rozpatrywanymi ciałami; r2 - to odległość na płaszczyźnie między tymi ciałami, przyjęta jako kwadrat; k to współczynnik proporcjonalności (
dla próżni).
Kierunek działania siły Coulomba i postać wektorowa wzoru
Aby w pełni zrozumieć wzór, prawo Coulomba można przedstawić w formie wizualnej:
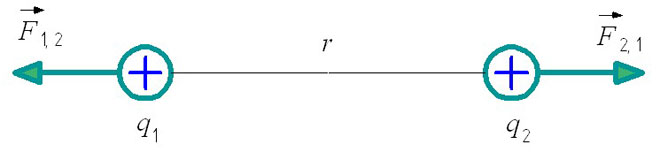
F1,2 - to siła oddziaływania pierwszego ładunku na drugi.
F2,1 - to siła oddziaływania drugiego ładunku względem pierwszego.
Przy rozwiązywaniu zadań z elektrostatyki należy również wziąć pod uwagę zasadę, że ładunki podobne odpychają się, a ładunki podobne przyciągają. Określa to położenie sił interakcji na rysunku.
Jeśli rozpatrujemy ładunki przeciwne, siły oddziaływania będą skierowane ku sobie, co oznacza ich przyciąganie.
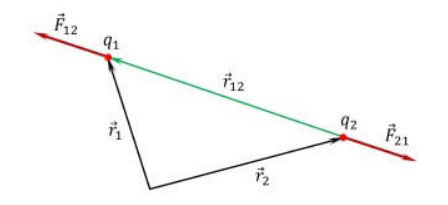
Wzór na podstawowe prawo elektrostatyki można przedstawić w postaci wektorowej w następujący sposób
- Siła działająca na ładunek punktowy q1, po stronie ładunku q2,
- jest wektorem promienia łączącym ładunek q2 z ładunkiem q1,
Ważne! Zapisując wzór w postaci wektorowej, trzeba będzie rzutować na oś oddziałujące siły dwóch punktowych ładunków elektrycznych, aby prawidłowo postawić znaki. Czynność ta jest formalnością i często jest wykonywana mentalnie, bez żadnych notatek.
Gdzie prawo Coulomba ma zastosowanie w praktyce
Podstawowe prawo elektrostatyki jest najważniejszym odkryciem Charlesa Coulomba, które znalazło zastosowanie w wielu dziedzinach.
Prace słynnego fizyka zostały wykorzystane w procesie wynalezienia różnych urządzeń, przyrządów i aparatów. Na przykład piorunochron.
Piorunochrony służą do ochrony domów i budynków przed wyładowaniami atmosferycznymi podczas burz. Zwiększa to stopień ochrony urządzeń elektrycznych.
Piorunochrony działają zgodnie z następującą zasadą: podczas burzy na ziemi stopniowo gromadzą się silne ładunki indukcyjne, które są następnie przenoszone w górę, w kierunku chmur. Powoduje to powstanie dużego pola elektrycznego na ziemi. W pobliżu piorunochronu pole elektryczne staje się silniejsze, co powoduje, że z końcówki urządzenia zapala się ładunek elektryczny w postaci korony.
Ładunek powstały na ziemi jest przyciągany do ładunku na chmurze z przeciwnym znakiem, tak jak powinno być zgodnie z prawem Coulomba. Powietrze ulega wówczas procesowi jonizacji, a natężenie pola elektrycznego zmniejsza się w pobliżu końca piorunochronu. Dzięki temu ryzyko uderzenia pioruna w budynek jest minimalne.
Uwaga! Jeśli budynek, na którym zainstalowano piorunochron, zostanie uderzony, nie dojdzie do pożaru, a cała energia ucieknie do ziemi.
W oparciu o prawo Coulomba opracowano urządzenie zwane "akceleratorem cząstek", które jest obecnie bardzo poszukiwane.
Urządzenie to wytwarza silne pole elektryczne, co zwiększa energię cząstek, które do niego wpadają.
Kierunek działania sił w prawie Coulomba
Jak już wspomniano, kierunek sił wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych zależy od ich biegunowości. Oznacza to, że ładunki podobne o tej samej polaryzacji będą się odpychać, a ładunki o przeciwnej polaryzacji będą się przyciągać.
Siły Coulomba można również nazwać wektorem promienia, ponieważ są one skierowane wzdłuż linii poprowadzonej między nimi.
W niektórych zagadnieniach fizyki dane są ciała o złożonym kształcie, które nie mogą być traktowane jako punktowy ładunek elektryczny, tzn. ich wymiary są pomijane. W takiej sytuacji dane ciało należy podzielić na kilka małych części i każdą z nich obliczyć osobno, stosując prawo Coulomba.
Wektory sił otrzymane w wyniku ich rozbicia sumuje się zgodnie z zasadami algebry i geometrii. Wynikiem jest siła wypadkowa, która jest odpowiedzią na problem. Ta metoda rozwiązania jest często nazywana metodą trójkąta.
Historia odkrycia prawa
Oddziaływanie dwóch ładunków punktowych zgodnie z powyższym prawem zostało po raz pierwszy udowodnione w 1785 r. przez Charlesa Coulomba. Fizykowi udało się udowodnić prawdziwość sformułowanego prawa za pomocą wag skrętnych, których zasada działania została również przedstawiona w artykule.
Coulomb udowodnił również, że wewnątrz kondensatora kulistego nie ma ładunku elektrycznego. W ten sposób doszedł do stwierdzenia, że wielkość sił elektrostatycznych można zmieniać, zmieniając odległość między danymi ciałami.
Prawo Coulomba jest więc nadal najważniejszym prawem elektrostatyki, na podstawie którego dokonano wielu wielkich odkryć. W niniejszym artykule przedstawiono oficjalne sformułowanie ustawy oraz szczegółowo opisano jej części składowe.
Powiązane artykuły:
