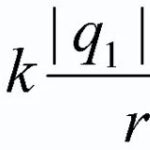Lorentzova síla a pravidlo levé ruky. Pohyb nabitých částic v magnetickém poli

Vodič umístěný v magnetickém poli vodičkterým prochází elektrický proud elektrický proudje ovlivněna Ampérovou silou $F_A$ a jeho velikost lze vypočítat podle následujícího vzorce

$F_A=B\cdot I\cdot l\cdot sin\alfa$ (1)

kde $I$ и $l$ - proudu a délky vodiče, $B$ - indukce magnetického pole, $\alfa$ - úhel mezi směry proudu a magnetické indukce. Proč se to děje?

Lorentzova síla. Pohyb nabité částice v magnetickém poli.

Obsah

1 Co je to Lorentzova síla - definice, kdy vzniká, získání vzorce
2 Určení směru Lorentzovy síly pomocí pravidla levé ruky
3 Pohyb nabité částice v magnetickém poli
4 Použití Lorentzovy síly ve strojírenství

Co je Lorentzova síla - definice, kdy vzniká, odvození vzorce

Je známo, že elektrický proud je uspořádaný pohyb nabitých částic. Je také známo, že při pohybu v magnetickém poli působí na každou z těchto částic síla. Aby mohla vzniknout síla, musí být částice v pohybu.

Lorentzova síla je síla, která působí na elektricky nabitou částici při jejím pohybu v magnetickém poli. Jeho směr je kolmý na rovinu, v níž leží vektory rychlosti částice a intenzity magnetického pole. Lorentzova síla je Ampérova síla. S jeho znalostí lze odvodit vzorec pro Lorentzovu sílu.

Doba, za kterou částice projde určitým úsekem vodiče, $t = \frac {l}{v}$ kde $l$ - je délka úseku, $v$ - rychlost částice. Celkový náboj přenesený za tuto dobu přes průřez vodiče, $Q = I\cdot t$ . Nahradíme-li zde časovou hodnotu z předchozí rovnice, dostaneme následující hodnoty.

$Q = \frac {I\cdot l}{v}$ (2)

Současně $F_A = F_L\\cdot N$ kde $N$ - je počet částic v uvažovaném vodiči. Současně $N = \frac {Q}{q}$ kde $q$ - je náboj jedné částice. Dosazením do vzorce $Q$ z (2) lze získat:

$N = \frac {I\cdot l}{v\cdot q}$

Tedy,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Pomocí (1) lze předchozí výraz zapsat jako

$B\cdot I\cdot l\cdot sin\alfa = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Po řezech a převodech získáme vzorec pro výpočet Lorentzovy síly

$F_L = q\cdot v\cdot B\cdot sin\alfa$

Vzhledem k tomu, že vzorec je zapsán pro modul síly, měl by být zapsán takto:

Přečtěte si také: Jak převést ampéry na watty a zpět?

$F_L = |q||\cdot v\cdot B\cdot sin\alfa$ (3)

Vzhledem k tomu, že $sin\alfa = sin(180^{\circ} - \alfa)$ , pro výpočet Lorentzova modulu nezáleží na tom, zda je rychlost ve směru proudu nebo proti němu, a můžeme říci, že $\alfa$ - je úhel, který svírají vektory rychlosti částice a magnetické indukce.

Zápis vzorce ve vektorovém tvaru bude vypadat takto:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}].$

$[\vec{v}\krát \vec{B}]$ - je vektorový součin, jehož výsledkem je vektor s modulem rovným $v\cdot B\cdot sin\alfa$ .

Ze vzorce (3) vyplývá, že Lorentzova síla je maximální v případě kolmosti směrů elektrického proudu a magnetického pole, tj. v bodě (3). $\alfa = 90^{\circ}$ a zmizí při jejich rovnoběžnosti ( $\alfa = 0^{\\circ}$ ).

Je třeba mít na paměti, že pro správnou kvantitativní odpověď - například při řešení problému - je třeba používat jednotky SI, v nichž se magnetická indukce měří v teslech (1 tesla = 1 kg-c).⁻²-А⁻¹), síla v newtonech (1 N = 1 kg-m/s).²), proud v ampérech, náboj v coulonech (1 Cl = 1 A-s), délka v metrech, rychlost v m/s.

Určení směru Lorentzovy síly pomocí pravidla levé ruky

Protože ve světě makroobjektů se Lorentzova síla projevuje jako Ampérova síla, můžeme k určení jejího směru použít pravidlo levé ruky.

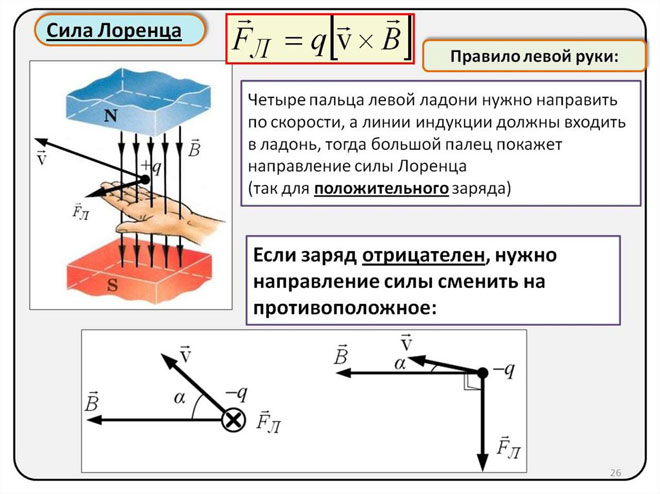
Určení směru Lorentzovy síly pomocí pravidla levé ruky.

Levá ruka je umístěna kolmo k magnetickým siločarám a směřuje k nim, čtyři prsty by měly být nataženy ve směru proudu, pak Lorentzova síla bude směřovat tam, kam směřuje palec, který by měl být ohnutý.

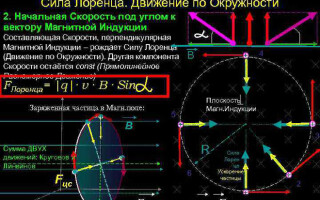
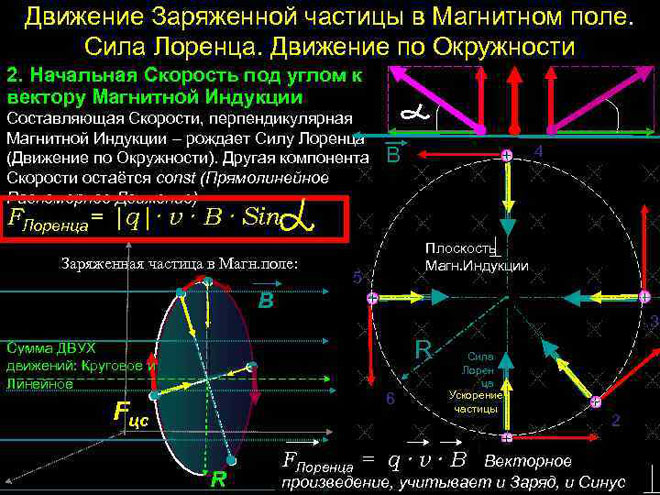
Pohyb nabité částice v magnetickém poli

V nejjednodušším případě, tj. při ortogonalitě vektorů magnetické indukce a rychlosti částice, může Lorentzova síla, která je kolmá na vektor rychlosti, měnit pouze jeho směr. Velikost rychlosti, tedy i energie, zůstane nezměněna. Lorentzova síla tedy působí obdobně jako dostředivá síla v mechanice a částice se pohybuje po kružnici.

Přečtěte si také: Kolik wattů je v kilowattu?

Podle druhého Newtonova zákona ( $F = m\cdot a$ ) lze určit poloměr rotace částice:

$N = \frac {m\cdot v}{q\cdot B}$ .

Je třeba poznamenat, že se změnou měrného náboje částice ( $\frac {q}{m}$ ) se mění i poloměr.

Tedy perioda otáčení T = . $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Nezávisí na rychlosti, takže vzájemná poloha částic s různými rychlostmi bude stejná.

Pohyb nabité částice v homogenním magnetickém poli.

Ve složitějším případě, kdy je úhel mezi rychlostí částice a intenzitou magnetického pole libovolný, se bude pohybovat po šroubovité trajektorii - postupně na úkor složky rychlosti směřující rovnoběžně s polem a obkročmo na úkor její kolmé složky.

Aplikace Lorentzovy síly ve strojírenství

Kinescope

Kineskop, který byl až donedávna, kdy byl nahrazen LCD (plochou obrazovkou), součástí každého televizoru, by bez Lorentzovy síly nemohl fungovat. K vytvoření televizního obrazu na obrazovce slouží úzké proudy elektronů, které jsou vychylovány cívkami generujícími lineárně se měnící magnetické pole. Řadové cívky pohybují elektronovým svazkem zleva doprava a zpět, zatímco rámové cívky jsou zodpovědné za vertikální pohyb a pohybují běžícím svazkem horizontálně shora dolů. Stejný princip se používá v osciloskopy - přístroje používané ke studiu střídavého elektrického napětí.

Hmotnostní spektrograf

Hmotnostní spektrograf je přístroj, který využívá vztahu mezi poloměrem rotace nabité částice a jejím specifickým nábojem. Jeho princip fungování je následující:

Zdroj nabitých částic, které nabývají rychlosti pomocí uměle vytvořeného elektrického pole, je umístěn ve vakuové komoře, aby se eliminoval vliv molekul vzduchu. Částice vylétají ze zdroje a po kružnici dopadají na fotografickou desku, na které zanechávají stopy. V závislosti na konkrétním náboji se mění poloměr trajektorie, a tedy i místo dopadu. Tento poloměr lze snadno změřit a na základě jeho znalosti lze vypočítat hmotnost částice. Pomocí hmotnostního spektrografu bylo například studováno složení měsíční půdy.

Přečtěte si také: Jaké profese jsou spojeny s elektřinou

Cyklotron

Nezávislost periody, a tedy i frekvence rotace nabité částice na její rychlosti v přítomnosti magnetického pole se využívá v přístroji zvaném cyklotron, který je určen k urychlování částic na vysoké rychlosti. Cyklotron se skládá ze dvou dutých kovových půlválců, duantů (každý ve tvaru latinského písmene D), umístěné rovnými stranami proti sobě v malé vzdálenosti.

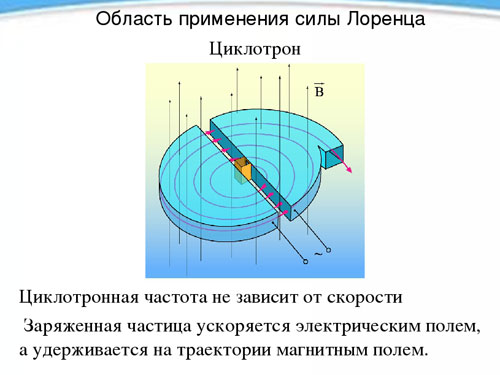
Cyklotron - aplikace Lorentzovy síly.

Duanty jsou umístěny v konstantním homogenním magnetickém poli a je mezi nimi vytvořeno střídavé elektrické pole, jehož frekvence je rovna rotační frekvenci částice, která je určena intenzitou magnetického pole a specifickým nábojem. Částice je během rotace dvakrát ovlivněna elektrickým polem (při přechodu z jednoho duantu do druhého), pokaždé je urychlena, čímž se zvětší poloměr trajektorie, a v určitém okamžiku, když získá potřebnou rychlost, vyletí otvorem ven ze zařízení. Tímto způsobem lze urychlit proton na energii 20 MeV.megaelektronvolt).

Magnetron

Zařízení zvané magnetron, které je instalováno v každém mikrovlnná troubaje dalším příkladem přístroje, který funguje na základě Lorentzovy síly. Magnetron vytváří silné mikrovlnné pole, které ohřívá vnitřní prostor trouby, v němž je umístěn pokrm. Magnety v magnetronu upravují dráhu elektronů uvnitř pece.

Magnetické pole Země

Lorentzova síla je v přírodě pro lidstvo velmi důležitá. Jeho přítomnost umožňuje zemskému magnetickému poli chránit člověka před smrtícím ionizujícím zářením ve vesmíru. Pole zabraňuje bombardování povrchu planety nabitými částicemi a nutí je měnit směr.

Související články: