अधिष्ठापन क्या है, इसे कैसे मापा जाता है, मूल सूत्र

प्रेरण एक विद्युत सर्किट में चुंबकीय क्षेत्र ऊर्जा को संग्रहीत करने के लिए घटकों की क्षमता का एक उपाय है। यह वर्तमान और चुंबकीय क्षेत्र के बीच संबंध का एक उपाय भी है। इसकी तुलना बिजली की जड़ता से भी की जाती है, क्योंकि द्रव्यमान यांत्रिक निकायों की जड़ता का एक माप है।

आत्म-प्रेरण की घटना

यदि किसी चालक परिपथ से प्रवाहित धारा परिमाण में भिन्न होती है, तो स्व-प्रेरण की घटना घटित होती है। इस मामले में, सर्किट के माध्यम से चुंबकीय प्रवाह बदल जाता है, और एक ईएमएफ जिसे सेल्फ-इंडक्शन ईएमएफ कहा जाता है, वर्तमान फ्रेम की ओर बढ़ता है। यह EMF धारा की दिशा के विपरीत है और इसके बराबर है:

ε=-∆F/∆t=-L*(∆I/∆t)

जाहिर है, स्व-प्रेरण ईएमएफ सर्किट के माध्यम से बहने वाले प्रवाह में परिवर्तन के कारण चुंबकीय प्रवाह में परिवर्तन की दर के बराबर है, और वर्तमान में परिवर्तन की दर के समानुपाती भी है।स्व-प्रेरण के ईएमएफ और धारा के परिवर्तन की दर के बीच आनुपातिकता के गुणांक को अधिष्ठापन कहा जाता है और इसे एल द्वारा दर्शाया जाता है। यह मान हमेशा सकारात्मक होता है, और इसमें 1 हेनरी (1 जीएन) की एसआई इकाई होती है। भिन्नात्मक भिन्नों, मिलीजेनरीज और माइक्रोजेनरीज का भी उपयोग किया जाता है। हम 1 हेनरी के इंडक्शन की बात कर सकते हैं यदि 1 एम्पीयर के करंट में बदलाव से 1 वोल्ट का ईएमएफ सेल्फ-इंडक्शन होता है। न केवल एक सर्किट में इंडक्शन होता है, बल्कि एक एकल कंडक्टर और एक कॉइल भी होता है, जिसे श्रृंखला में सर्किट के एक सेट के रूप में दर्शाया जा सकता है।

ऊर्जा को अधिष्ठापन में संग्रहित किया जाता है, जिसकी गणना W=L*I . के रूप में की जा सकती है²/2, जहां:

• डब्ल्यू - ऊर्जा, जे;
• एल - अधिष्ठापन, जीएन;
• मैं - कॉइल में करंट, ए।

और यहाँ ऊर्जा सीधे कुंडली के अधिष्ठापन के समानुपाती होती है।

महत्वपूर्ण! इंजीनियरिंग में, अधिष्ठापन उस उपकरण को भी संदर्भित करता है जिसमें विद्युत क्षेत्र संग्रहीत होता है। इस परिभाषा के निकटतम वास्तविक तत्व एक प्रारंभ करनेवाला कुंडल है।

भौतिक कुंडल के अधिष्ठापन की गणना के लिए सामान्य सूत्र का एक जटिल रूप है और व्यावहारिक गणना के लिए असुविधाजनक है। यह याद रखना उपयोगी है कि अधिष्ठापन घुमावों की संख्या, कुंडल के व्यास के समानुपाती होता है और ज्यामितीय आकार पर निर्भर करता है। इसके अलावा इंडक्शन कोर की चुंबकीय पारगम्यता से प्रभावित होता है जिस पर कॉइल स्थित होता है, लेकिन कॉइल के माध्यम से बहने वाली धारा से प्रभावित नहीं होता है। अधिष्ठापन की गणना करने के लिए, हर बार आपको किसी विशेष डिज़ाइन के लिए दिए गए सूत्रों का उल्लेख करना होगा। इस प्रकार, एक बेलनाकार कुंडल के लिए, इसकी मूल विशेषता की गणना सूत्र के अनुसार की जाती है:

एल=μ*μ*(एन²*एस/एल),

कहाँ पे:

• μ कुंडल कोर की सापेक्ष चुंबकीय पारगम्यता है;
• μ - चुंबकीय स्थिरांक, 1.26*10-6 Gn/m;
• एन - घुमावों की संख्या;
• एस - कुंडल का क्षेत्र;
• एल - कुंडल की ज्यामितीय लंबाई।

एक बेलनाकार कुंडल और अन्य कुंडल आकृतियों के लिए अधिष्ठापन की गणना करने के लिए, ऑनलाइन कैलकुलेटर सहित कैलकुलेटर कार्यक्रमों का उपयोग करना बेहतर है।

श्रृंखला और समानांतर में जोड़ने वाले अधिष्ठापन

नई विशेषताओं के साथ एक सेट का निर्माण करते हुए, इंडक्शन को श्रृंखला या समानांतर में जोड़ा जा सकता है।

समानांतर कनेक्शन

जब कॉइल समानांतर में जुड़े होते हैं, तो सभी तत्वों पर वोल्टेज बराबर होता है और धाराएं (बारी) तत्वों के अधिष्ठापन के व्युत्क्रमानुपाती होते हैं।

• यू = यू₁=यू₂=यू₃;
• मैं = मैं₁+मैं₂+मैं₃.

सर्किट का कुल अधिष्ठापन 1/L=1/L . के रूप में परिभाषित किया गया है₁+1/ली₂+1/ली₃. सूत्र किसी भी संख्या में तत्वों के लिए मान्य है, और दो कॉइल के लिए इसे एल = एल के रूप में सरल बनाया गया है₁*ली₂/(एल₁+एल₂) यह स्पष्ट है कि परिणामी अधिष्ठापन सबसे कम वाले तत्व के अधिष्ठापन से कम है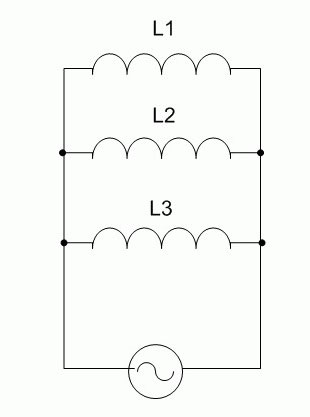

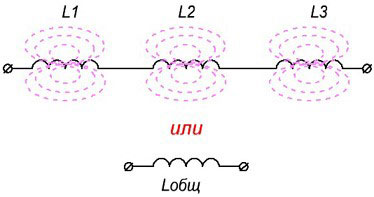
श्रृंखला कनेक्शन

इस प्रकार के कनेक्शन के साथ, कॉइल से बने सर्किट के माध्यम से एक ही धारा प्रवाहित होती है, और सर्किट के प्रत्येक घटक पर वोल्टेज (एसी!) प्रत्येक तत्व के अधिष्ठापन के अनुपात में वितरित किया जाता है:

• यू = यू₁+उ₂+उ₃;
• मैं = मैं₁=मैं₂=मैं₃.

कुल अधिष्ठापन सभी अधिष्ठापन के योग के बराबर है, और उच्चतम मूल्य वाले तत्व के अधिष्ठापन से अधिक होगा। इसलिए, इस कनेक्शन का उपयोग तब किया जाता है जब अधिष्ठापन में वृद्धि प्राप्त करना आवश्यक हो।

महत्वपूर्ण! श्रृंखला या समानांतर बैटरी में कॉइल्स को कनेक्ट करते समय, गणना सूत्र केवल उन मामलों के लिए सही होते हैं जहां तत्वों के चुंबकीय क्षेत्रों के पारस्परिक प्रभाव को एक दूसरे पर बाहर रखा जाता है (परिरक्षण, बड़ी दूरी, आदि)। यदि प्रभाव मौजूद है, तो अधिष्ठापन का कुल मूल्य कुंडलियों की पारस्परिक व्यवस्था पर निर्भर करेगा।

प्रारंभ करनेवाला कॉइल के कुछ व्यावहारिक मुद्दे और डिजाइन

व्यवहार में प्रारंभ करनेवाला कॉइल के विभिन्न डिजाइनों का उपयोग किया जाता है। डिवाइस के उद्देश्य और अनुप्रयोग के आधार पर विभिन्न तरीकों से बनाया जा सकता है, लेकिन वास्तविक कॉइल में होने वाले प्रभावों पर विचार करना आवश्यक है।

एक प्रारंभ करनेवाला कुंडल का गुणवत्ता कारक

एक वास्तविक कॉइल में इंडक्शन के अलावा कई पैरामीटर होते हैं, और सबसे महत्वपूर्ण में से एक गुणवत्ता कारक है। यह मान कॉइल में नुकसान को निर्धारित करता है और इस पर निर्भर करता है:

• घुमावदार तार में ओमिक नुकसान (प्रतिरोध जितना अधिक होगा, गुणवत्ता कारक उतना ही कम होगा);
• तार के इन्सुलेशन और घुमावदार के फ्रेम में ढांकता हुआ नुकसान;
• ढाल में नुकसान;
• कोर नुकसान।

ये सभी मात्राएँ हानि प्रतिरोध को परिभाषित करती हैं, और गुणवत्ता कारक Q=ωL/R हानि के बराबर एक आयाम रहित मान है, जहाँ:

• ω = 2*π*F - वृत्ताकार आवृत्ति;
• एल - अधिष्ठापन;
• L - कुंडल प्रतिक्रिया।

हम मोटे तौर पर कह सकते हैं कि गुणवत्ता कारक सक्रिय प्रतिरोध के प्रतिक्रियाशील (आगमनात्मक) प्रतिरोध के अनुपात के बराबर है। एक ओर, बढ़ती आवृत्ति के साथ अंश बढ़ता है, लेकिन साथ ही त्वचा के प्रभाव के कारण उपयोगी तार क्रॉस-सेक्शन की कमी के कारण हानि प्रतिरोध भी बढ़ जाता है।

त्वचा का प्रभाव

विदेशी वस्तुओं के साथ-साथ विद्युत और चुंबकीय क्षेत्रों के प्रभाव को कम करने और इन क्षेत्रों के माध्यम से तत्वों के पारस्परिक प्रभाव को कम करने के लिए, कॉइल (विशेष रूप से उच्च आवृत्ति वाले) को अक्सर ढाल में रखा जाता है। उपयोगी प्रभाव के अलावा, परिरक्षण कुंडल क्यू-कारक में कमी का कारण बनता है, इसके अधिष्ठापन को कम करता है और परजीवी समाई में वृद्धि करता है। इसके अलावा, ढाल की दीवारें कॉइल के जितने करीब आती हैं, हानिकारक प्रभाव उतना ही अधिक होता है। इसलिए, परिरक्षित कॉइल लगभग हमेशा मापदंडों के समायोजन की संभावना के साथ बनाए जाते हैं।

समायोज्य अधिष्ठापन

कुछ मामलों में, ट्यूनिंग के दौरान मापदंडों के विचलन की भरपाई के लिए, सर्किट के अन्य तत्वों को कॉइल को जोड़ने के बाद, इंडक्शन वैल्यू को ठीक से सेट करना आवश्यक है। इसके लिए विभिन्न तरीकों का उपयोग किया जाता है (मोड़ बदलना, आदि), लेकिन सबसे सटीक और आसान तरीका कोर के साथ समायोजन है।इसे एक थ्रेडेड रॉड के रूप में बनाया जाता है, जिसे कॉइल के इंडक्शन को एडजस्ट करते हुए फ्रेम के अंदर और बाहर स्क्रू किया जा सकता है।

चर अधिष्ठापन (वैरोमीटर)

जहां इंडक्शन या इंडक्टिव कपलिंग के परिचालन समायोजन की आवश्यकता होती है, कॉइल के एक अलग डिजाइन का उपयोग किया जाता है। इनमें दो वाइंडिंग, एक मूविंग वाइंडिंग और एक स्थिर वाइंडिंग होती है। कुल अधिष्ठापन दो कुंडलियों के अधिष्ठापन और उनके बीच पारस्परिक अधिष्ठापन के योग के बराबर है।

एक कॉइल की सापेक्ष स्थिति को दूसरे में बदलकर, कुल अधिष्ठापन मूल्य समायोजित किया जाता है। इस तरह के एक उपकरण को वेरोमीटर कहा जाता है और अक्सर संचार उपकरण में अनुनाद सर्किट ट्यूनिंग के लिए उपयोग किया जाता है जहां किसी कारण से परिवर्तनीय क्षमता के कैपेसिटर्स का उपयोग असंभव है। वेरोमीटर काफी बोझिल है, जो इसके आवेदन के क्षेत्र को सीमित करता है।

बॉल वेरोमीटर

एक मुद्रित कुंडल के रूप में अधिष्ठापन

कम इंडक्शन वाले कॉइल मुद्रित कंडक्टरों के सर्पिल के रूप में बनाए जा सकते हैं। इस तरह के डिजाइन के फायदे हैं:

• विनिर्माण क्षमता;
• मापदंडों की उच्च दोहराव।

नुकसान समायोजन के दौरान ठीक ट्यूनिंग की असंभवता और अधिष्ठापन के बड़े मूल्यों को प्राप्त करने में कठिनाई है - अधिष्ठापन जितना अधिक होगा, कुंडल बोर्ड पर उतना ही अधिक स्थान लेता है।

अनुभागीय घुमावदार के साथ कुंडल

समाई के बिना अधिष्ठापन केवल कागज पर होता है। कॉइल के किसी भी भौतिक कार्यान्वयन के साथ, तुरंत एक परजीवी अंतर-घुमावदार समाई होती है। यह कई मामलों में एक हानिकारक घटना है। आवारा समाई एलसी-सर्किट की समाई को जोड़ती है, गुंजयमान आवृत्ति और दोलन प्रणाली के गुणवत्ता कारक को कम करती है। इसके अलावा कुंडल की अपनी गुंजयमान आवृत्ति होती है, जो अवांछनीय घटनाओं को भड़काती है।

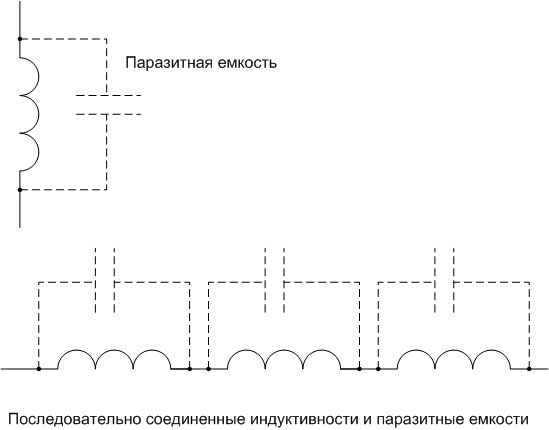
आवारा समाई को कम करने के लिए, विभिन्न विधियों का उपयोग किया जाता है, जिनमें से सबसे सरल श्रृंखला में जुड़े कई वर्गों के रूप में प्रेरकों की वाइंडिंग है। इस कनेक्शन के साथ, अधिष्ठापन जोड़े जाते हैं, और कुल समाई कम हो जाती है।

टॉरॉयडल कोर पर इंडक्शन कॉइल

बेलनाकार कुंडल चुंबकीय क्षेत्र रेखाएं

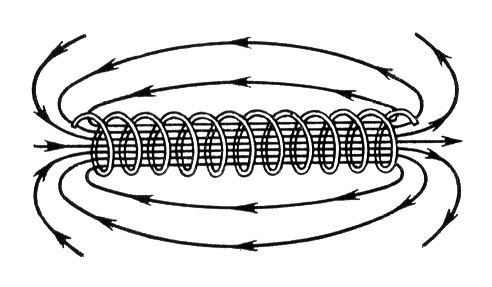
एक बेलनाकार प्रारंभ करनेवाला कुंडल की चुंबकीय क्षेत्र रेखाएं कुंडल के अंदर से गुजरती हैं (यदि कोई कोर है, तो इसके माध्यम से) और हवा के माध्यम से छोटा हो जाता है। इस तथ्य के कई नुकसान हैं:

• अधिष्ठापन कम हो गया है;
• कुंडल की विशेषताएं कम गणना योग्य हैं;
• बाहरी चुंबकीय क्षेत्र में पेश की गई कोई भी वस्तु कुंडल मापदंडों (अधिष्ठापन, परजीवी समाई, हानि, आदि) को बदल देती है, इसलिए कई मामलों में परिरक्षण की आवश्यकता होती है।

टॉरॉयडल कोर (अंगूठी या "बैगेल" के रूप में) पर घाव वाले कॉइल इन कमियों से काफी हद तक मुक्त होते हैं। क्रोड के अंदर चुंबकीय रेखाएं बंद लूपों के रूप में चलती हैं। इसका मतलब यह है कि बाहरी वस्तुओं का ऐसे कोर पर कुंडल घाव के मापदंडों पर लगभग कोई प्रभाव नहीं पड़ता है, और इस तरह के डिजाइन के लिए परिरक्षण आवश्यक नहीं है। इसके अलावा, अधिष्ठापन में वृद्धि हुई है, अन्य सभी पैरामीटर समान हैं, और विशेषताओं की गणना करना आसान है।

टॉरॉयडल कॉइल की चुंबकीय क्षेत्र रेखाएं

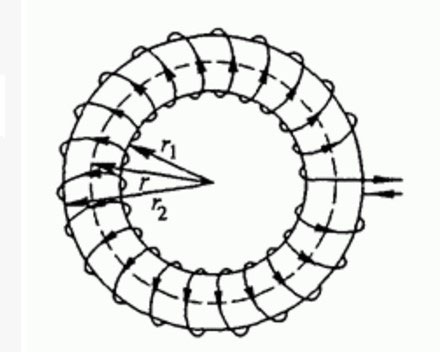
टॉरस पर कॉइल घाव के नुकसान में जगह में अधिष्ठापन को सुचारू रूप से समायोजित करने में असमर्थता शामिल है। एक अन्य समस्या उच्च श्रम तीव्रता और घुमावदार की कम विनिर्माण क्षमता है। हालाँकि, यह सामान्य रूप से सभी आगमनात्मक तत्वों पर अधिक या कम सीमा तक लागू होता है।

इसके अलावा अधिष्ठापन के भौतिक कार्यान्वयन का एक सामान्य नुकसान उच्च द्रव्यमान आयाम, अपेक्षाकृत कम विश्वसनीयता और कम रखरखाव है।

इसलिए, प्रौद्योगिकी में, आगमनात्मक घटकों से छुटकारा पाने की कोशिश की जाती है। लेकिन यह हमेशा संभव नहीं होता है, इसलिए निकट भविष्य में और मध्यम अवधि में घुमावदार घटकों का उपयोग किया जाएगा।

इंडक्शन ईएमएफ क्या है और यह कब होता है?

विद्युत समाई क्या है, इसे किसमें मापा जाता है और यह किस पर निर्भर करता है

ट्रांसफॉर्मर का परिवर्तन अनुपात कितना होता है?

पारगम्यता क्या है

श्रृंखला या समानांतर में कैपेसिटर की समाई का निर्धारण - सूत्र

प्रत्यावर्ती विद्युत धारा की सक्रिय और प्रतिक्रियाशील शक्ति क्या है?